Rekurze je využití sebe sama. Příkladem je použití pojmu při jeho vlastní definici nebo obrázek obsahující svoji zmenšenou kopii. Rekurzivní funkce je taková funkce, která pro výpočet využívá sebe sama (s jinými hodnotami parametrů). Využití rekurze často vede k elegantnímu řešení problému. Některé programovací jazyky využívají rekurzi jako základní prostředek pro opakování příkazů (místo cyklů).
Faktoriál – příklad rekurzivní definice
Faktoriál čísla n (značí se n!) je součin čísel 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n. Například 4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24. Faktoriál lze definovat rekurzivně:
0! = 1
n! = n \cdot (n - 1)! \text{ pro } n > 0
Nejedná se o definici v kruhu, protože při aplikování definice dochází ke zjednodušování (faktoriál n je definován pomocí faktoriálu n - 1) a je definován i bázový případ (n = 0) bez rekurze, ke kterému vše směřuje. Jde tedy spíše o definici ve spirále.
Rekurzivní šroubování žárovky
A: Kolik otoček potřebuji na zašroubování žárovky?
B: Pokud už je zašroubovaná, tak 0. Jinak ji zatoč jednou, zeptej se mě znova a k mé odpovědi přičti 1.
Návrh rekurzivních algoritmů
Nejprve určíme podproblémy, které potřebujeme k vyřešení našeho problému (např. pro výpočet faktoriálu n potřebujeme znát faktoriál n - 1). Tyto podproblémy vyřešíme rekurzivně (tedy voláním funkce s jinými parametry) a z výsledků poskládáme výsledné řešení. Dále je nutné určit bázový případ a jeho řešení (např. faktoriál 0 je 1). Bázový případ musí být takový, aby se k němu všechny větve výpočtu časem dostaly, jinak by výpočet nikdy neskončil.
Sebe-reference
Rekurze je příkladem obecnějšího jevu odkazování na sebe sama, tzv. sebe-reference. Sebe-reference se vyskytuje v jazyce (Třeba tato věta mluví sama o sobě.), knihách, divadle, filmu i matematice. Sebe-reference je dokonce hlavní ingrediencí snad nejslavnějších důkazů matematiky (Gödelovy věty o neúplnosti) a také informatiky (existence problémů, pro které neexistuje algoritmus, který by je řešil – např. úloha určit, zda daný program někdy zastaví).
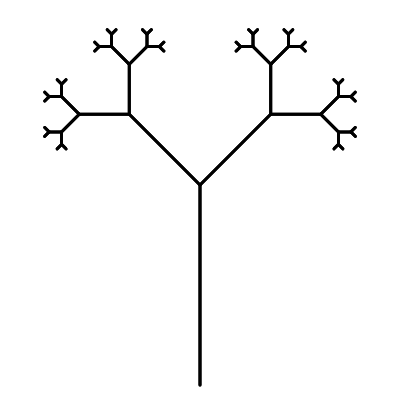
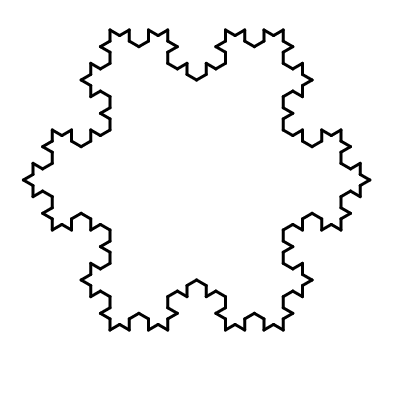
Fraktály
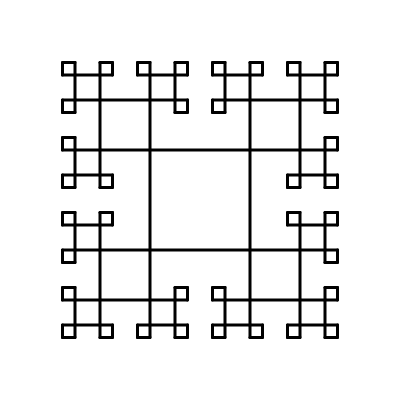
Vedle rekurze jsou nejtypičtějším zástupcem sebe-reference fraktály – obrázky, které jsou soběpodobné, tedy jejich části připomínají obrázek jako celek. Fraktály lze často vidět v přírodě (např. větve stromů, kapradina). Fraktály a rekurze nejsou dva nezávislí reprezentanti sebe-reference, i mezi nimi je silná souvislost. Rekurze je totiž velmi elegantní způsob, jak různé fraktály definovat. Díky tomu často můžeme složité fraktály vykreslit pomocí jednoduchých rekurzivních funkcí.
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.

Vybarvování: rekurze a fraktály (střední) • NTG
zadání: 23
Typicky zabere: 5 min
Stavitel
Pomocí blokového programování vytvořte program pro stavitele Standu.
Rekurze
Bonusová sada, ve které nejsou dostupné bloky pro opakování. Místo toho je potřeba vhodně využít rekurzivní funkce (funkce, které volají sami sebe).
Robotanik
Jednoduché grafické ovládání, zapeklité programátorské úlohy.
Těžké
Tady už to začíná být komplikovanější. U těchto příkladů už je často potřeba využít naplno princip rekurze (zanořování a vynořování z funkcí).
Opravdová výzva
Tyto úlohy už mohou dát zabrat i zkušenému programátorovi.
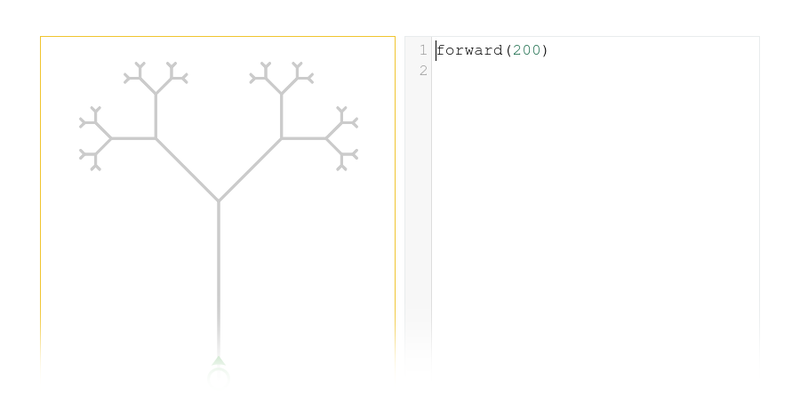
Python želva
Tvorba programů v Pythonu, kreslení obrázků želví grafikou.
Rekurze a fraktály
Náročné, bonusové téma pro pokročilé. Za využití rekurze můžeme pomocí želví grafiky kreslit elegantní fraktály. Jde to často krátkým programem, který však vůbec není lehké vymyslet...


 Čeština
Čeština Matematika
Matematika Angličtina
Angličtina Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV