Regrese (v kontextu strojového učení) je úloha odhadnout číselnou hodnotu nějaké veličiny v závislosti na jednom či více atributech (např. odhadování ceny bytu na základě jeho rozlohy). Lineární regrese je řešení regresní úlohy pomocí lineárního modelu, tedy modelu, který je lineární funkcí (tj. váženým součtem) optimalizovaných parametrů.
Nejjednodušším příkladem lineární regrese je hledání přímky \hat{y} = ax + b, která co nejlépe popisuje vztah mezi souřadnicemi x a y zadaných bodů D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}. V případě výše je x rozloha, y skutečná cena bytu a \hat{y} odhad ceny podle modelu. Model má dva parametry (a, b), které je potřeba určit (učení modelu, optimalizace).
Kvadratická chyba
Abychom mohli vybrat „nejlepší“ přímku, musíme stanovit chybovou funkci popisující, jak dobře daná přímka odpovídá zadaným bodům. Nejčastěji se používá kvadratická chyba, definovaná jako součet druhých mocnin odchylek jednotlivých odhadů oproti skutečnosti. Tento přístup se označuje jako metoda nejmenších čtverců, protože minimalizujeme součet druhých mocnin, tedy čtverců. Chyba závisí na parametrech a, b a množině bodů D:
E(a, b, D) = \sum_{(x,y) \in D} (\hat{y} - y)^2 = \sum_{(x,y) \in D} (ax + b - y)^2
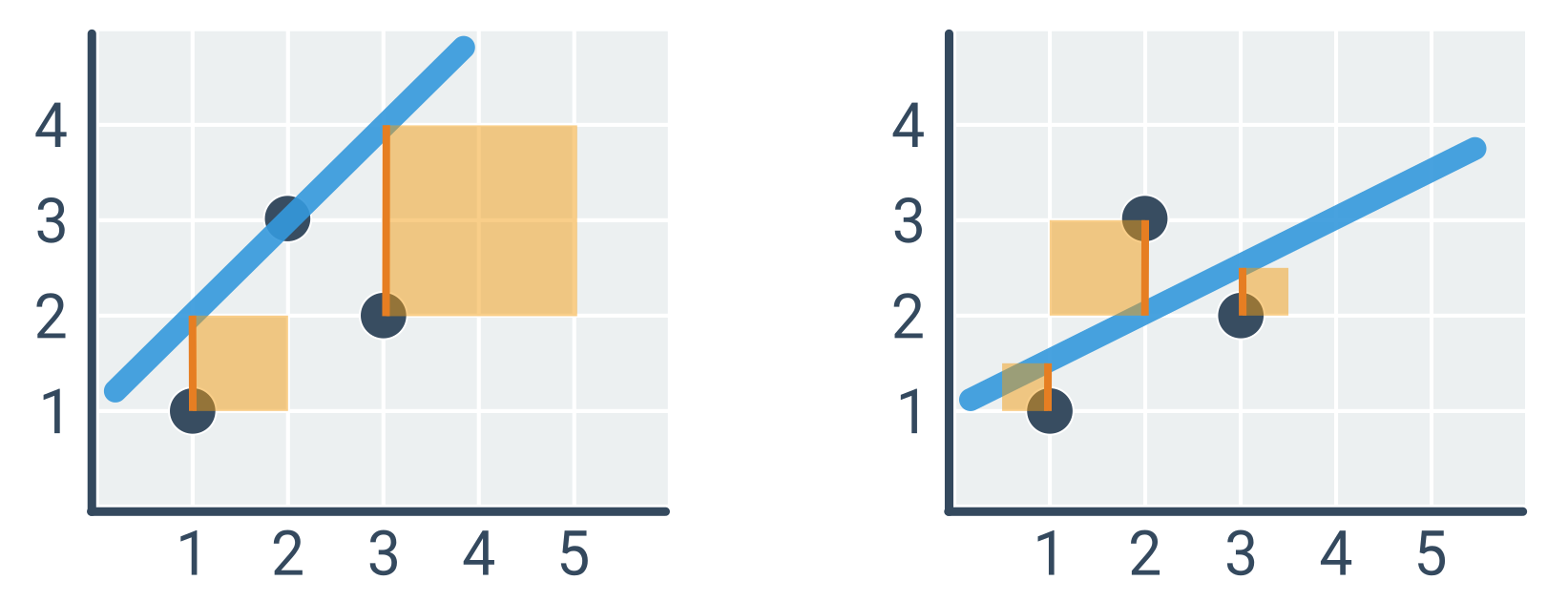
Přímka vlevo (\hat{y} = x + 1) má kvadratickou chybu 1^2 + 2^2 = 5, zatímco přímka vpravo (\hat{y} = 0{,}5x + 1) pouze 0{,}5^2 + 1^2 + 0{,}5^2 = 1{,}5.
Kvadratická chyba je vzhledem k mocnění odchylek citlivá na odlehlé body (outliery), tedy body, které leží daleko od ostatních. Někdy se proto odlehlé body odstraňují, v každém případě je o nich dobré vědět.
Optimalizace parametrů
Úlohou je tedy najít takové hodnoty parametrů a, b, které minimalizují kvadratickou chybu. K optimalizaci existuje řada obecných přístupů, např. systematické zkoušení různých kombinací hodnot parametrů (hrubá síla), nebo postupné vylepšování jedné kombinace parametrů drobnými úpravami (gradientní sestup). V případě lineární regrese lze však optimální parametry určit analyticky, tj. přímým výpočtem pomocí následujících vzorců:
a = \frac{\sum (x - \bar{x})(y - \bar{y})}{\sum (x - \bar{x})^2}
b = \bar{y} - a\bar{x}
Sumy \sum značí součet přes všechny body (x, y) \in D. \bar{x}, \bar{y} jsou průměrné hodnoty x a y. Směrnice a je tedy tím vyšší, čím je mezi x a y silnější vztah a čím jsou odchylky y větší relativně vůči odchylkám x. Rovnici pro b dostáváme z intuitivního vztahu mezi průměrnými hodnotami: \bar{y} = a\bar{x} + b. (Vzorce lze odvodit skrze derivaci kvadratické chybové funkce, která musí být v minimu rovna 0.)
Příklad výpočtu optimální přímky
Hledáme parametry a, b pro body na obrázku výše, tedy D = \{(1, 1), (2, 3), (3, 2)\}.
- \bar{x} = 2, \bar{y} = 2
- (x - \bar{x}) = [-1, 0, 1]
- (y - \bar{y}) = [-1, 1, 0]
- \sum (x - \bar{x})(y - \bar{y}) = (-1) \cdot (-1) + 0 \cdot 1 + 1 \cdot 0 = 1
- \sum (x - \bar{x})^2 = (-1)^2 + 0^2 + 1^2 = 2
- a = 1 / 2 = 0{,}5
- b = \bar{y} - a\bar{x} = 2 - 0{,}5 \cdot 2 = 1
Optimální přímka je tedy \hat{y} = 0{,}5x + 1 (což odpovídá obrázku vpravo).
Obecná lineární regrese
Atributů, na základě kterých děláme odhady, je typicky více. Lineární model má pak parametr pro každý atribut. Například chceme odhadovat rychlost zvířete na základě jeho váhy a délky končetin:
\hat{y} = w_0 + w_1 x_1 + w_2 x_2
\hat{y} je odhad rychlosti, x_1 je váha, x_2 je délka končetin a w_i jsou parametry modelu, které se učíme (jako a, b v případě modelu s jedním atributem). Pro výpočet optimálních parametrů existuje vzorec, který je zobecněním výše uvedených vzorců pro přímku.
Lineární model může mít členy i pro nelineární transformace atributů. Například bychom pro odhad rychlosti zvířete mohli využít druhou mocninu jeho váhy: \hat{y} = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1^2. Důležité je, že funkce je lineární vzhledem k parametrům w_i, protože ostatní hodnoty jsou konkrétní čísla odvozená z atributů příkladu.
Lineární modely jsou dobře interpretovatelné. Čím vyšší je absolutní hodnota parametru, tím vyšší má přidružený atribut vliv na odhadovanou hodnotu. Pokud je parametr kladný, pak s rostoucí hodnotou atributu roste odhadovaná hodnota, zatímco pokud je parametr záporný, pak s rostoucí hodnotou atributu odhadovaná hodnota klesá.










