







Skvěle, štít %% dosažen
Prohledávání stavového prostoru » Rozhodovačka »
Prohledávání stavového prostoru
Rozhodovačka
QR kód
Kód / krátká adresa
Zkopírujte kliknutím. Zkopírováno!
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
umime.to/NFS
Prohledávání stavového prostoru
Prohledávání stavového prostoru je základem mnoha technik umělé inteligence, využívá se například pro řešení logických úloh, výběr optimálního tahu, hledání nejkratší cesty nebo plánování akcí robota.
Stavový prostor úlohy se skládá ze stavů (možné konfigurace úlohy) a akcí (přechody mezi stavy). Jeden ze stavů je počáteční a alespoň jeden stav je cílový. Přechody mohou mít přidruženou cenu.
Stavový prostor jako graf
Stavový prostor lze reprezentovat ohodnoceným orientovaným grafem, jehož vrcholy odpovídají stavům a hrany akcím. Graf stavového prostoru je pro většinu praktických úloh příliš velký na to, abychom ho celý zkonstruovali v paměti, ale některé prohledávací algoritmy si postupně budují část tohoto grafu.
Plán je libovolná posloupnost akcí. Řešení úlohy je takový plán, který nás dostane z počátečního stavu do cílového. Optimální řešení je řešení, které má nejnižší cenu. (Cena plánu je nejčastěji součet cen jednotlivých přechodů.)
Příklad stavového prostoru (skřítek na mřížce)
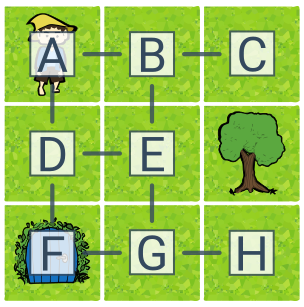
Úlohou je dostat skřítka do domečku. Stavový prostor úlohy má 8 stavů (A–H) a 4 akce (doleva, doprava, dolů, nahoru). Počáteční stav je A, cílový stav F. Optimálním řešením úlohy je např. plán dolů–dolů. Příkladem řešení, které není optimální, je doprava–dolů–dolů–doleva.
Zkoušení všech možností
Nejjednodušším algoritmem, který najde řešení vždy (pokud existuje) je generuj a testuj. Tento algoritmus generuje všechny možné plány a testuje, zda jde o řešení úlohy. Jde tedy o využití hrubé síly, techniky návrhu algoritmů založené na zkoušení všech možností. Zásadní nevýhodou hrubé síly je její časová náročnost. Počet plánů roste exponenciálně vzhledem k délce plánu.
Kolik je různých plánů?
Pokud máme 4 různé akce (P – doprava, D – dolů, L – doleva, H – nahoru), tak existují 4 plány délky 1, ale již 4^2 plánů délky 2 (PP, PD, PL, PH, DP, DD, DL, DH, LP, LD, LL, LH, HP, HD, HL, HH), 4^3 plánů délky 3, 4^4 plánů délky 4, atd.
Obecně, plánů délky n s k akcemi je k^n. Například pro 3 možné akce existuje plánů o 5 krocích 3^5 = 243, plánů o 6 krocích třikrát více, 3^6 = 729, a plánů o 20 krocích je 3^{20}, což už je několik miliard.
Stromové prohledávání
Mnohé plány však nemusí být vůbec proveditelné, nebo se opakovaně vracejí do stejného stavu. Je proto výhodnější testovat plány průběžně po každé akci – jakmile se dostaneme do slepé uličky nebo dříve prozkoumaného stavu, nemusíme žádné další plány začínající touto posloupností akcí prozkoumávat.
Stromové prohledávání je obecný název pro takový způsob prohledávání, kdy postupně konstruujeme a vyhodnocujeme plány po každé akci. Postup prohledávání plánů lze popsat prohledávacím stromem, ve kterém vrcholy reprezentují plány (a současně stav, do kterého se vykonáním plánu dostaneme) a orientované hrany reprezentují akce, které rozšiřují předchozí plán o jeden krok. Prohledávací strom zachycuje stavový prostor tak, jak ho postupně objevuje prohledávací algoritmus. Existuje několik variant stromového prohledávání, které se liší v tom, který plán rozšiřují (tj. který z objevených stavů prozkoumávají jako další):
Prohledávání do hloubky (DFS, angl. Depth First Search) vybírá poslední objevený stav. DFS má dobrou paměťovou složitost, protože si pamatuje pouze plány na aktuální větvi prohledávacího stromu.
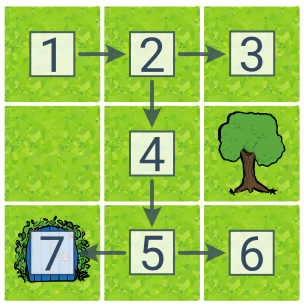
V této ukázce předpokládáme, že DFS zkouší akce po směru hodinových ručiček (doprava–dolů–doleva–nahoru). Čísla u stavů popisují pořadí objevení. Cíl byl nalezen v 7. kroce a nalezený plán má 4 kroky (doprava–dolů–dolů–doleva).
Prohledávání do šířky (BFS, angl. Breadth First Search) prohledává stavy po vrstvách podle počtu akcí od počátečního stavu. To sice zvyšuje paměťovou složitost (je potřeba si pamatovat více stavů), ale vede k nalezení nejkratšího řešení.
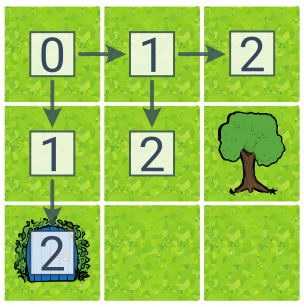
Čísla u stavů v ukázce BFS zachycují vzdálenosti od počátečního stavu, což odpovídá pořadí procházení „po vrstvách“. BFS našlo optimální řešení (dolů–dolů) po prozkoumání 6 stavů.
Prohledávání podle ceny (UCS, angl. Uniform Cost Search) je variací BFS, které umožňuje nalézt nejlevnější řešení, i když mají akce různou cenu. K rozšíření vybíráme plán s nejnižší cenou.
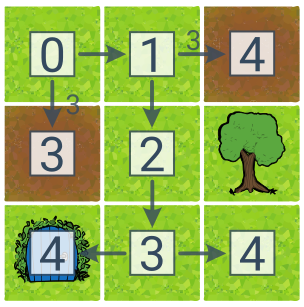
Pro ukázku UCS jsme přidali do plánku dvě hnědé bažiny s třikrát vyšší cenou přechodů. Čísla ve čtverečcích zde zachycují cenu plánu. V tomto případě je nejlevnější řešení (s cenou 4) doprava–dolů–dolů–doleva a UCS ho nalezne. (BFS by vrátilo řešení dolů–dolů s cenou 6.)
Algoritmus stromového prohledávání
Při stromovém prohledávání si udržujeme množinu stavů, které chceme v budoucnu prozkoumat, tzv. okraj. V každém kroku jeden stav z okraje odebereme a do okraje zařadíme jeho následníky (tj. stavy, do kterých se lze dostat z odebíraného stavu jednou akcí). Obecné schéma stromového prohledávání je následovné:
- Zařaď do okraje počáteční stav.
- Opakuj následující kroky, dokud nenajdeš cíl.
- Odeber jeden stav z okraje. Pokud je cílový, skonči.
- Jinak ho expanduj, tj. zařaď do okraje jeho následníky.
- Pokud se vyprázdnil okraj, tak cesta do cíle neexistuje.
Zmíněné varianty stromového prohledávání se liší tím, jakou strategii využívají k výběru stavu z okraje (krok 3), tj. jak implementují okraj. Prohledávání do hloubky (DFS) používá zásobník (odebíráme naposledy vložený stav), prohledávání do šířky (BFS) frontu (odebíráme nejdříve vložený stav) a prohledávání podle ceny (UCS) prioritní frontu (odebíráme stav s nejnižší cenou zatím nejlevnějšího plánu vedoucího do daného stavu).
Abychom se vyhnuli opakovanému prozkoumávání stejných stavů, můžeme si navíc udržovat množinu již prozkoumaných stavů a ty znova neexpandovat. Toto rozšíření se někdy označuje jako obecné grafové prohledávání, aby se odlišilo od stromového prohledávání bez kontroly dříve prozkoumaných stavů. Nevýhodou je zvýšení paměťové náročnosti.
Informované prohledávání
Prohledávání lze urychlit pomocí heuristik poskytujících odhad vzdálenosti do cíle. Taková informace je závislá na konkrétní úloze. Prohledávání využívající heuristiky označujeme jako informované prohledávání. (Algoritmy v předchozích sekcích označujeme naopak jako „neinformované“.)
Hladové prohledávání se řídí pouze hodnotou heuristiky a vybírá vždy akci, která nás dostane nejblíže cíli. Pokud hrozí slepé uličky, je potřeba hladový přístup zkombinovat se stromovým prohledáváním (jde tedy o tzv. hladové stromové prohledávání) – jako další stav vybíráme ten s nejnižším odhadem ceny podle heuristiky. Hladové prohledávání je velmi rychlé, negarantuje však nalezení optimálního řešení.
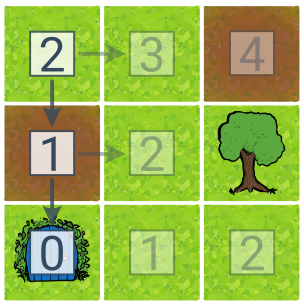
V této ukázce stromového hladového prohledávání odpovídají čísla u stavů heuristickému odhadu ceny do cíle. Heuristikou je vzdálenost od cíle spočítaná jako součet odchylek sloupce a řádku. Algoritmus našel cestu do cíle během dvou kroků, nikoliv však cestu nejlevnější.
A* prohledávání („A star“) kombinuje prohledávání podle ceny (UCS) s heuristikou. Jde o stromové prohledávání, kdy jako další stav vybíráme takový, který má nejnižší součet dosavadní ceny a heuristického odhadu zbývající ceny do cíle. Pokud je heuristika optimistická (poskytuje dolní odhad skutečné ceny), pak A* nelezne optimální řešení a nalezne ho tím rychleji, čím těsnější odhady skutečné ceny heuristika poskytuje.
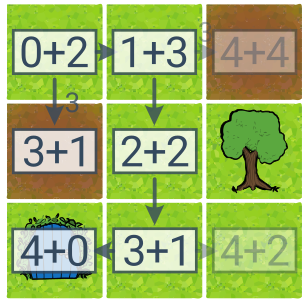
Součet u stavů popisuje prioritu pro A*: [dosavadní cena] + [odhad zbývající ceny]. A* našlo optimální řešení a prozkoumalo přitom méně stavů než UCS (6 místo 8).
Prohledávání stavového prostoru (těžké)

