Pravděpodobnost umožňuje pracovat s nejistotou, která je ve strojovém učení nevyhnutelná, neboť model musí odhadovat odpovědi i pro nové příklady, které nikdy předtím neviděl.

Bayesova věta

Často umíme snadno určit P(B \mid A), kde A způsobuje nebo ovlivňuje B, ale zajímá nás opačná podmíněná pravděpodobnost P(A \mid B). Z posbíraných dat umíme snadno vypočítat pravděpodobnost, že e-mail obsahuje slovo „zázračný“, pokud jde o spam, ale pro klasifikaci e-mailů potřebujeme znát opačnou podmíněnou pravděpodobnost – pravděpodobnost, že jde o spam, když text obsahuje slovo „zázračný“. V takových případech lze podmíněnou pravděpodobnost „otočit“ podle Bayesovy věty:

P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}

Vzorec lze také vnímat jako update původní (nepodmíněné) pravděpodobnosti P(A) (prior) s přihlédnutím k nové informaci, že nastal jev B. Zpřesněná (podmíněná) pravděpodobnost P(A \mid B) se pak označuje jako posterior.

Pravděpodobnostní klasifikátor

Pravděpodobnostní modely lze nejsnáze využít pro řešení klasifikačních úloh (např. rozhodnout, zda je daný e-mail spam). Označme X příklad, který chceme klasifikovat, X_1, X_2, \ldots, X_n jeho jednotlivé atributy (např. přítomnost různých slov v textu e-mailu) a Y možné kategorie (spam / normální e-mail). Chceme predikovat kategorii s větší podmíněnou pravděpodobností P(Y \mid X). Tyto pravděpodobnosti můžeme spočítat s využitím Bayesovy věty:

P(Y \mid X) = P(X \mid Y) \cdot P(Y) \mathbin{/} P(X)

Zatímco určení P(Y) je snadné (spočítáme, jaký podíl e-mailů v trénovacích datech jsou spam), určení P(X \mid Y) vyžaduje exponenciálně mnoho příkladů vzhledem k počtu atributů (potřebovali bychom e-maily se všemi možnými kombinacemi uvažovaných slov). Možným řešením je pravděpodobnostní rozdělení odhadovat pouze přibližně pomocí nějakého modelu, který nemá exponenciální počet parametrů (např. neuronová síť).

Naivní Bayesův klasifikátor

Pro mnohé jednoduché problémy však stačí výrazně jednodušší řešení: předpokládat, že jednotlivé atributy jsou na sobě podmíněně nezávislé (při znalosti kategorie). Pak nám totiž stačí n jednoparametrických podmíněných pravděpodobností:

P(Y \mid X) = P(Y) \cdot P(X_1 \mid Y) \cdot P(X_2 \mid Y) \cdot \ldots \cdot P(X_n \mid Y) \mathbin{/} P(X)

Tento model se označuje jako Naivní Bayesův klasifikátor. Slovo „naivní“ se odkazuje právě na předpoklad podmíněné nezávislosti atributů, který typicky neplatí (např. přítomnost slova „zázračný“ zvyšuje pravděpodobnosti slova „lék“ i pokud víme, že jde o spam). Odhadnuté pravděpodobnosti tak mohou být hodně nepřesné. Pro úspěšnou klasifikaci však není podstatné, zda jsou pravděpodobnosti odhadnuté přesně, ale zda má skutečná kategorie nejvyšší odhadnutou pravděpodobnost, což často platí. Výhodou je nízký počet parametrů (lineární vzhledem k počtu atributů), nízký počet příkladů potřebných k učení a také rychlé učení (přímočarý výpočet hodnot parametrů).

Bayesovské sítě

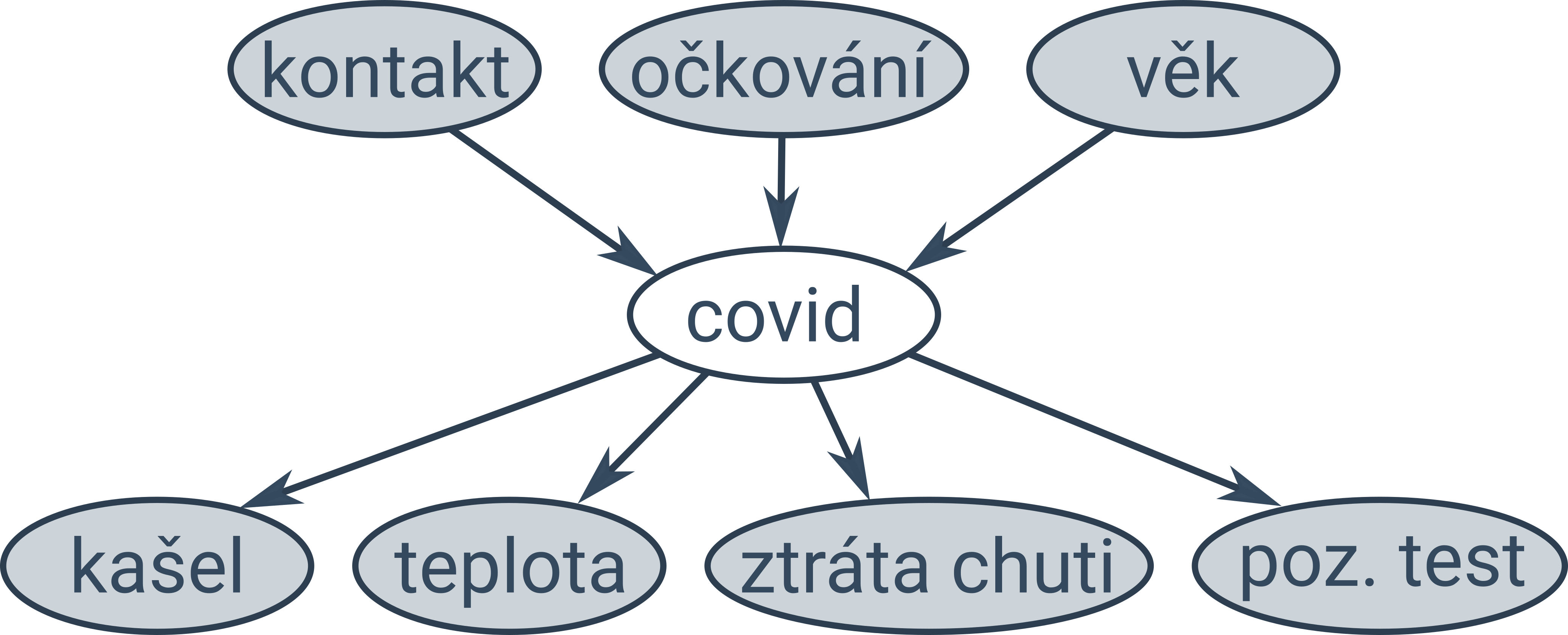
Naivní Bayesův klasifikátor předpokládá, že jsou všechny atributy podmíněně nezávislé. V některých případech víme, že některé atributy nezávislé jsou a jiné nejsou. Takovou situaci můžeme modelovat pomocí Bayesovských sítí, což je orientovaný graf zachycující vztahy mezi pozorovanými a skrytými proměnnými (pozorované proměnné jsou na obrázcích níže podbarvené šedě):

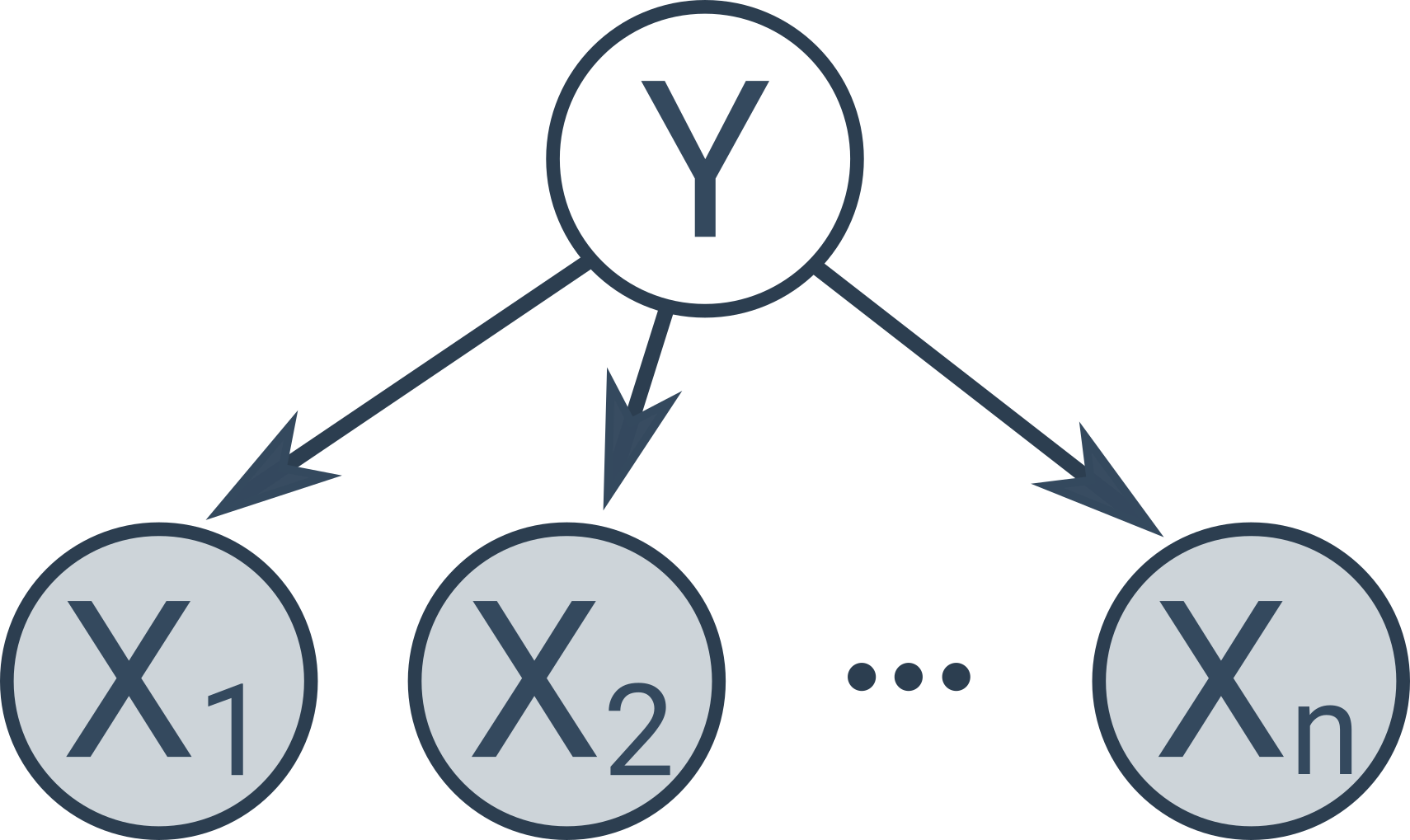
Naivní Bayesův klasifikátor je speciální typ Bayesovské sítě s následující jednoduchou strukturou:

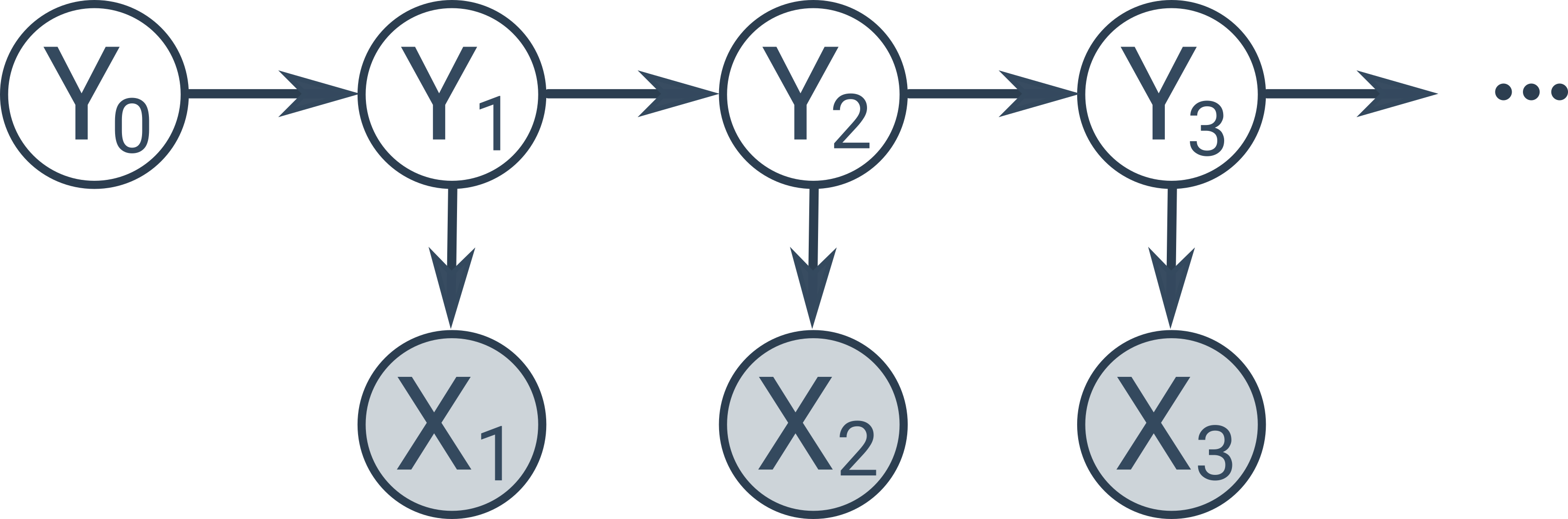
Existují další speciální typy Bayesovských sítí, např. skryté Markovovy modely, znázorňující časovou posloupnost skrytých stavů (poloha robota, vyslovovaný text), v níž každý stav závisí pouze na jednom předchozím stavu a produkuje pozorovatelné měření (měření ultrazvukového senzoru, zaznamenaný zvuk).