Metody strojového učení

Obecný postup strojového učení zahrnuje volbu výpočetního modelu pro řešení dané úlohy, jehož parametry poté učíme ve fázi trénování modelu. Témata v této kapitole podrobněji představují několik modelů, které se ve strojovém učení často využívají:

• lineární modely – určují výstup pomocí lineární funkce
• rozhodovací stromy – určují výstup pomocí řady podmínek
• neuronové sítě – kombinují velké množství jednoduchých funkcí (tzv. neuronů)
• pravděpodobnostní modely – pracují s nejistotou (např. Naivní Bayesův klasifikátor)

Regrese (v kontextu strojového učení) je úloha odhadnout číselnou hodnotu nějaké veličiny v závislosti na jednom či více atributech (např. odhadování ceny bytu na základě jeho rozlohy). Lineární regrese je řešení regresní úlohy pomocí lineárního modelu, tedy modelu, který je lineární funkcí (tj. váženým součtem) optimalizovaných parametrů.

Nejjednodušším příkladem lineární regrese je hledání přímky \hat{y} = ax + b, která co nejlépe popisuje vztah mezi souřadnicemi x a y zadaných bodů D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}. V případě výše je x rozloha, y skutečná cena bytu a \hat{y} odhad ceny podle modelu. Model má dva parametry (a, b), které je potřeba určit (učení modelu, optimalizace).

Kvadratická chyba

Abychom mohli vybrat „nejlepší“ přímku, musíme stanovit chybovou funkci popisující, jak dobře daná přímka odpovídá zadaným bodům. Nejčastěji se používá kvadratická chyba, definovaná jako součet druhých mocnin odchylek jednotlivých odhadů oproti skutečnosti. Tento přístup se označuje jako metoda nejmenších čtverců, protože minimalizujeme součet druhých mocnin, tedy čtverců. Chyba závisí na parametrech a, b a množině bodů D:

E(a, b, D) = \sum_{(x,y) \in D} (\hat{y} - y)^2 = \sum_{(x,y) \in D} (ax + b - y)^2

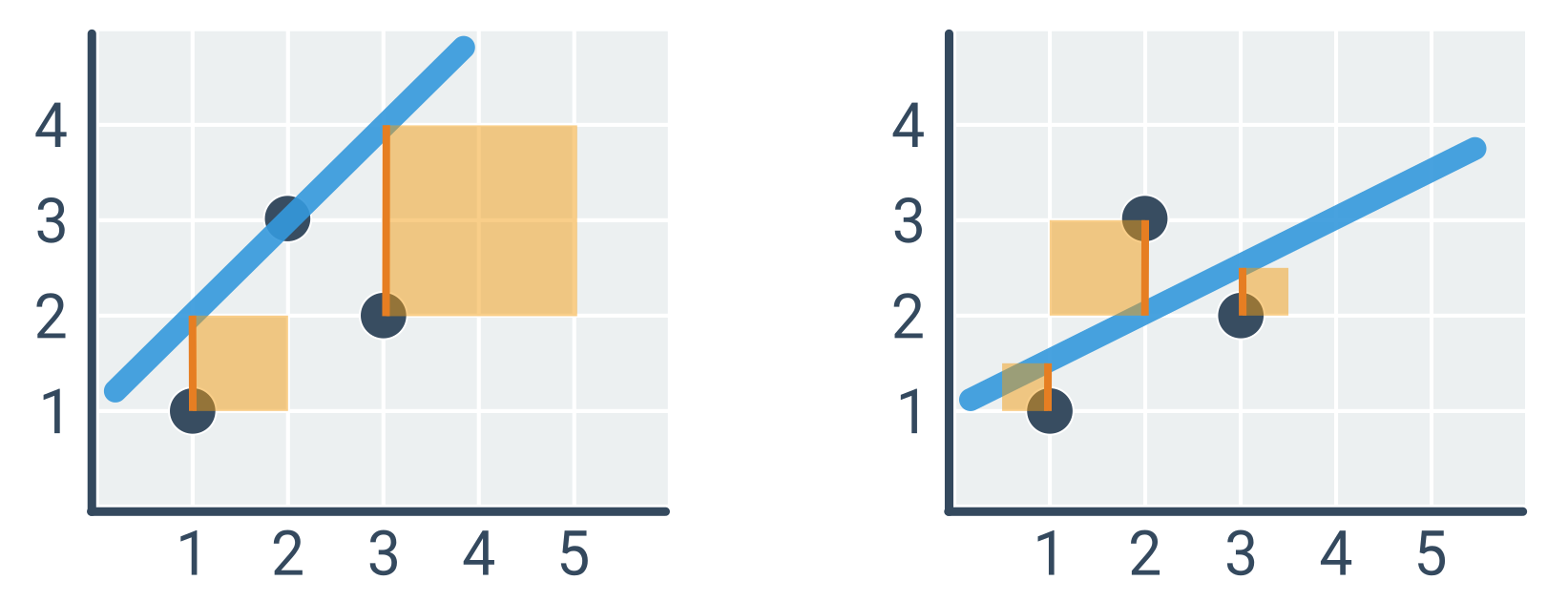
Přímka vlevo (\hat{y} = × + 1) má kvadratickou chybu 1^2 + 2^2 = 5, zatímco přímka vpravo (\hat{y} = 0{,}5x + 1) pouze 0{,}5^2 + 1^2 + 0{,}5^2 = 1{,}5.

Kvadratická chyba je vzhledem k mocnění odchylek citlivá na odlehlé body (outliery), tedy body, které leží daleko od ostatních. Někdy se proto odlehlé body odstraňují, v každém případě je o nich dobré vědět.

Optimalizace parametrů

Úlohou je tedy najít takové hodnoty parametrů a, b, které minimalizují kvadratickou chybu. K optimalizaci existuje řada obecných přístupů, např. systematické zkoušení různých kombinací hodnot parametrů (hrubá síla), nebo postupné vylepšování jedné kombinace parametrů drobnými úpravami (gradientní sestup). V případě lineární regrese lze však optimální parametry určit analyticky, tj. přímým výpočtem pomocí následujících vzorců:

a = \frac{\sum (x - \bar{x})(y - \bar{y})}{\sum (x - \bar{x})^2}

b = \bar{y} - a\bar{x}

Sumy \sum značí součet přes všechny body (x, y) \in D. \bar{x}, \bar{y} jsou průměrné hodnoty x a y. Směrnice a je tedy tím vyšší, čím je mezi x a y silnější vztah a čím jsou odchylky y větší relativně vůči odchylkám x. Rovnici pro b dostáváme z intuitivního vztahu mezi průměrnými hodnotami: \bar{y} = a\bar{x} + b. (Vzorce lze odvodit skrze derivaci kvadratické chybové funkce, která musí být v minimu rovna 0.)

Obecná lineární regrese

Atributů, na základě kterých děláme odhady, je typicky více. Lineární model má pak parametr pro každý atribut. Například chceme odhadovat rychlost zvířete na základě jeho váhy a délky končetin:

\hat{y} = w_0 + w_1 x_1 + w_2 x_2

\hat{y} je odhad rychlosti, x_1 je váha, x_2 je délka končetin a w_i jsou parametry modelu, které se učíme (jako a, b v případě modelu s jedním atributem). Pro výpočet optimálních parametrů existuje vzorec, který je zobecněním výše uvedených vzorců pro přímku.

Lineární model může mít členy i pro nelineární transformace atributů. Například bychom pro odhad rychlosti zvířete mohli využít druhou mocninu jeho váhy: \hat{y} = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1^2. Důležité je, že funkce je lineární vzhledem k parametrům w_i, protože ostatní hodnoty jsou konkrétní čísla odvozená z atributů příkladu.

Lineární modely jsou dobře interpretovatelné. Čím vyšší je absolutní hodnota parametru, tím vyšší má přidružený atribut vliv na odhadovanou hodnotu. Pokud je parametr kladný, pak s rostoucí hodnotou atributu roste odhadovaná hodnota, zatímco pokud je parametr záporný, pak s rostoucí hodnotou atributu odhadovaná hodnota klesá.

Rozhodovací strom (angl. decision tree) zachycuje proces rozhodování na základě postupně kladených otázek (podmínek). Rozhodování podle rozhodovacích stromů si můžete procvičit ve cvičení Deaktivace bomby: rozhodovací stromy. Rozhodovací stromy se využívají ve strojovém učení jako jeden z modelů, podobně jako třeba lineární modely nebo neuronové sítě.

Určení predikce podle rozhodovacího stromu

Proces rozhodování lze zachytit diagramem ve tvaru stromu (typ grafu), jehož vnitřní uzly obsahují podmínky a listy (koncové uzly, které se již nevětví) obsahují predikce. První podmínka je v kořenovém uzlu a dále postupujeme po hranách (šipkách) do levého nebo pravého podstromu podle toho, zda podmínka pro daný příklad platí, nebo neplatí. Cestu z kořene do listu lze interpretovat jako složenou podmínku spojenou s jedním klasifikačním pravidlem. Nejpravější větev následujícího stromu zachycuje pravidlo: „Pokud má příšerka alespoň 4 ruce a alespoň 5 očí, tak je zlá.“.

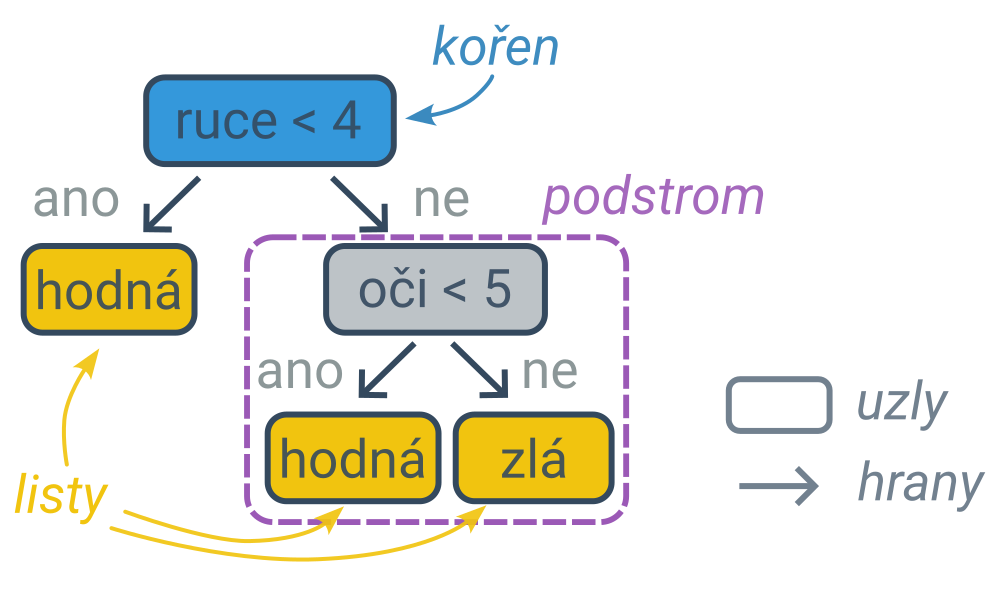
Rozhodovací stromy lze využít na řešení klasifikačních i regresních úloh. Klasifikační rozhodovací strom má v listech predikované kategorie, regresní klasifikační strom predikované číselné hodnoty.

Učení rozhodovacích stromů

V případě klasifikačních úloh hledáme takový rozhodovací strom, který maximalizuje správnost (počet správně klasifikovaných případů, angl. accuracy) na zadané trénovací množině příkladů. Možných stromů je příliš mnoho na to, abychom mohli vyzkoušet všechny, proto strom tvoříme postupným přidáváním uzlů s podmínkami. (Tento přístup, kdy děláme lokálně optimální rozhodnutí, která však negarantují celkově optimální výsledek, se označuje jako hladový algoritmus.)

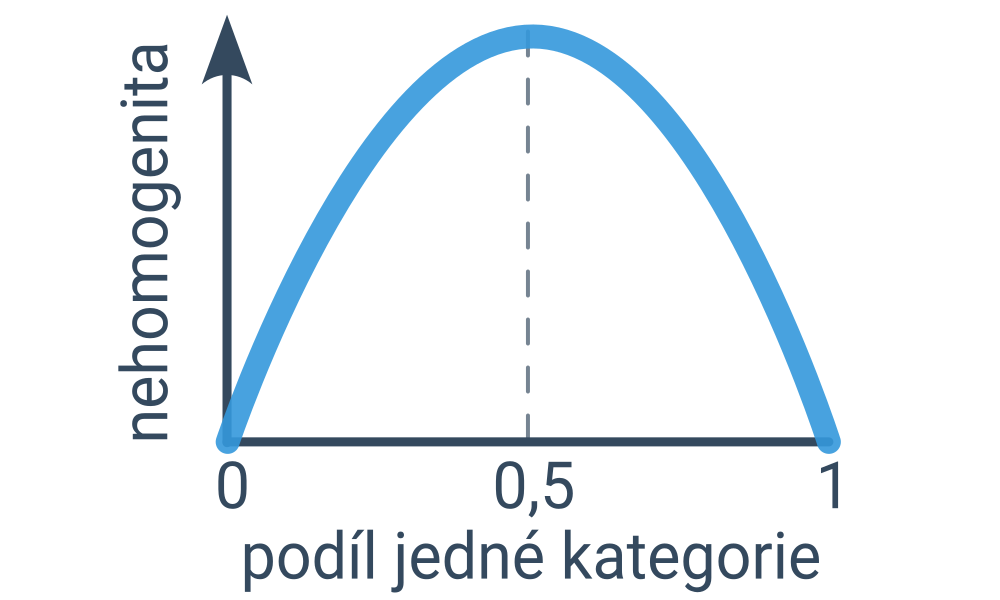
Začínáme s celým datasetem příkladů a hledáme podmínku, která rozdělí příklady na dvě co nejhomogenější skupiny. (Ideální podmínka by platila pro všechny příklady jedné kategorie a neplatila pro všechny příklady druhé kategorie – pak bychom totiž dosáhli nejvyšší možné správnosti predikcí.) Míru nehomogenity lze kvantifikovat například pomocí entropie nebo Gini indexu, což jsou podobné funkce, které jsou nulové pro zcela homogenní rozdělení a nejvyšší hodnotu mají pro rovnoměrné rozdělení (půlka příkladů z první kategorie, půlka příkladů z druhé kategorie).

Vybraná nejlepší podmínka se stává kořenem stromu. Stejný proces pak opakujeme pro každý podstrom, dokud dochází k zvyšování homogenity, dokud máme v uzlu dostatek příkladů a/nebo dokud strom není příliš hluboký. Predikce potom odpovídá nejčastější kategorii příkladů, které prošly do tohoto listu. (V případě regresních rozhodovacích stromů by to byla průměrná hodnota příkladů.)

Výhody a nevýhody rozhodovacích stromů

Rozhodovací stromy jsou jednoduché a velmi dobře interpretovatelné. Stromy lze přirozeně vizualizovat a pro jednotlivé predikce lze generovat jasná vysvětlení – složené podmínky dané cestou z kořene do listu. Tyto podmínky jsou navíc nad původními atributy, neboť rozhodovací stromy nevyžadují normalizaci atributů (oproti např. lineárním modelům). Rozhodovací stromy umožňují zachytit nelineární interakce mezi atributy, naopak však nedokáží efektivně zachytit lineární vztahy (jen přibližně pomocí velkého množství podmínek).

Rozhodovací stromy jsou náchylné k přeučení, čemuž lze předejít omezením hloubky a prořezáváním větví, které příliš nepřispívají k celkové správnosti predikcí. I při těchto opatřeních jsou však stromy nestabilní – malá změna dat může výrazně ovlivnit výsledný strom. Nestabilní jsou i jednotlivé predikce – malá změna jednoho atributu může způsobit skokovou změnu predikované hodnoty.

Rozšíření rozhodovacích stromů

Složitější modely kombinují více rozhodovacích stromů do jednoho modelu, aby zvýšili kvalitu predikcí. Náhodný les (angl. random forest) je agregace velkého množství rozhodovacích stromů naučených na náhodných podmnožinách trénovacích dat, jejichž predikce se průměrují. To zvyšuje stabilitu predikcí a snižuje náchylnost k přeučení. Nevýhodou je výrazně horší interpretovatelnost.

Neuronová síť je výpočetní model volně inspirovaný fungováním mozku. Skládá se z mnoha propojených neuronů, které počítají jednoduché funkce. Protože je ale neuronů hodně, je výsledná funkce určená neuronovou sítí složitá.

Neurony

Každý neuron přijímá signál z několika jiných neuronů, signály zpracuje a výsledek posílá dál do napojených neuronů. Signálem putujícím mezi dvěma neurony je jedno reálné číslo. Jednotlivé neurony počítají vážený součet vstupů upravený nelineární aktivační funkcí (např. \max(\cdot, 0)), tj. y = g(\sum_i w_i x_i), kde g je aktivační funkce, w jsou váhy a x jsou vstupní hodnoty.

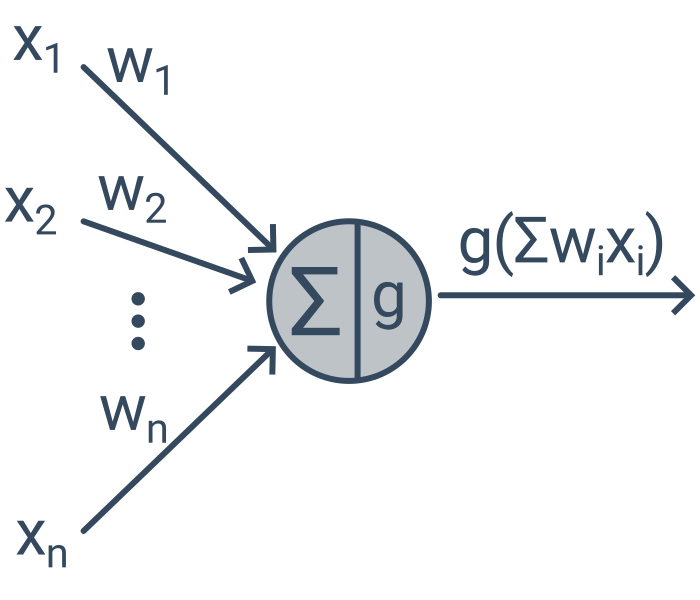
Perceptron je nejjednodušší neuronová síť – obsahuje jediný neuron. Taková síť je velmi podobná lineárnímu modelu. Většinou však neuronové sítě obsahují tisíce či miliony neuronů.

Struktura neuronové sítě

Neurony jsou typicky uspořádané do několika vrstev (vstupní, několik skrytých a nakonec výstupní). Příklad, o kterém chceme něco rozhodnout (např. obrázek, věta, stav hry), je zakódován pomocí hodnot neuronů ve vstupní vrstvě. Skryté vrstvy pak z příkladu extrahují postupně komplexnější vzory. (První skrytá vrstva například detekuje hrany a barevné pásy, druhá vrstva rohy a oblouky, další vrstva základní tvary, další vrstvy postup složitější tvary.) Výstupní vrstva pak obsahuje výslednou predikci (např. určení objektu na obrázku, pokračování rozepsané věty, vhodný tah). Pro neuronové sítě s mnoha vrstvami se používá označení hluboké.

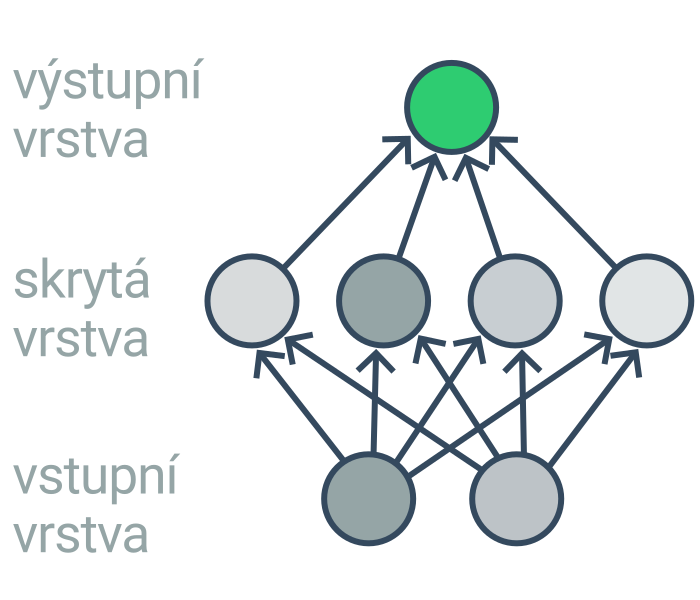
Základní architekturou je vícevrstvý perceptron, ve kterém jsou neurony v každé vrstvě propojeny se všemi neurony ve vrstvě následující. Alternativou jsou například konvoluční neuronové sítě, v nichž některé vrstvy provádí konvoluci – operaci, při které posouváme malý filtr přes celá data (např. každý pixel nahradíme váženým součtem pixelů v okolí). Konvoluční sítě se hodí na zpracování dat s prostorovou strukturou (např. obrázky).

Sítě, ve kterých informace putuje jedním směrem (tj. síť neobsahuje cykly) se označují jako dopředné. Opakem dopředných sítí jsou rekurentní neuronové sítě, které obsahují neurony, jejichž výstup je současně jejich vstupem (neuron má tedy v podstatě paměť). Rekurentní sítě se hodí pro zpracování sekvenčních dat (např. text). Výpočet a učení rekurentních neuronových sítí je však složitější než sítí dopředných.

Proto se v poslední době i pro sekvenční data častěji využívají trasnformátory, dopředné sítě, které transformují celé sekvence naráz a používají mechanismus pozornosti určující, na kterou část dosavadní sekvence se zaměřit. Transformátory se používají pro zpracování textu, zvuku i obrazu. (Např. GPT znamená „generativní předtrénovaný transformátor“.)

Učení neuronových sítí

Neuronová síť je v podstatě komplikovaná funkce s mnoha parametry (váhy mezi neurony). Učení sítě je optimalizační úloha hledání takových vah, které minimalizují chybu predikcí sítě na trénovacích datech. Příkladem chybové funkce je kvadratická chyba – součet druhých mocnin odchylek mezi predikovanou a skutečnou hodnotou (přes všechny příklady v trénovacích datech).

K učení se využívá algoritmus gradientního sestupu: začneme s náhodnými hodnotami parametrů a ty pak opakovaně upravujeme tak, abychom zmenšili chybu. Gradient je směr, ve kterém funkce nejrychleji roste, postupujeme tedy proti směru gradientu. Gradient lze spočítat algoritmem zpětného šíření chyby (angl. backpropagation): pro každý příklad v trénovací sadě provedeme dopředný výpočet sítě, porovnáme predikci se skutečností a upravíme všechny váhy (postupně od poslední k první vrstvě) tak, aby se chyba snížila.

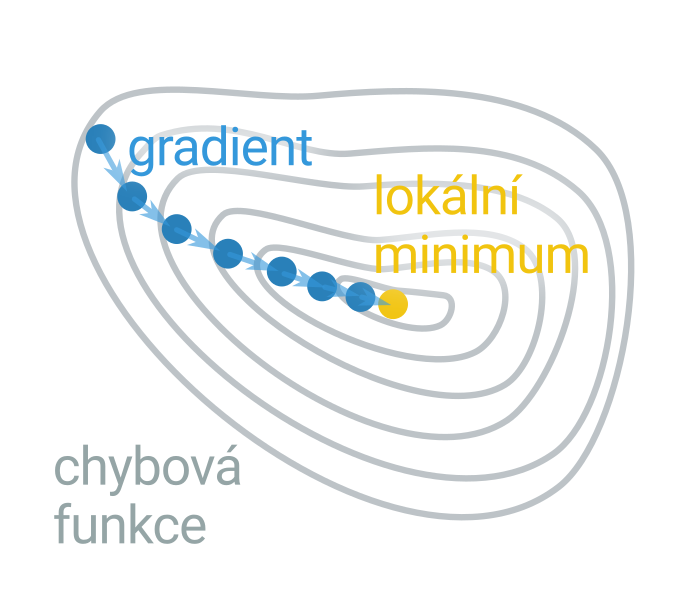
Učení hlubokých neuronových sítí je obtížné kvůli problému mizejícího gradientu – gradient exponenciálně klesá se vzdáleností neuronu od výstupu sítě. Výzkum v oblasti neuronových sítí přináší stále nové techniky, jak tento problém zmírnit, jako nejdůležitější se však ukazuje výpočetní výkon. Pro urychlení výpočtů se využívají grafické procesory (GPU, graphics processing unit) a tenzorové procesory (TPU, tensor processing unit), i tak však učení rozsáhlých modelů může trvat mnoho dní.

Neuronové sítě mají mnoho parametrů, hrozí proto riziko přeučení, kdy si síť pouze zapamatuje přesné odpovědi pro trénovací data, ale není schopna generalizovat na nové příklady. Pro učení neuronových sítí je proto potřeba velké množství příkladů a využití regularizačních technik, které riziko učení snižují (např. penalizace příliš vysokých vah).

Kromě vah v neuronové síti můžeme optimalizovat i její strukturu (např. počet vrstev) a parametry učení (např. velikost kroku při gradientním sestupu). Tyto speciální parametry ovlivňující ostatní parametry se označují jako hyperparametry. Jejich hodnota je během učení gradientním sestupem konstantní, můžeme je však optimalizovat mřížkovým prohledáváním, při kterém zkoušíme naučit síť pro různé volby hyperparametrů.

Využití

Neuronové sítě mají využití zejména v oblastech, kde je k dispozici velké množství dat k učení, je obtížné přesně popsat užitečné rysy příkladů manuálně a nepotřebujeme vysvětlení výsledných predikcí. Používají se pro zpracování přirozeného jazyka (odpovídání na otázky, strojový překlad, rozpoznávání řeči), počítačové vidění (klasifikace obrázků, generování obrázků, analýza medicínských měření), řízení a rozhodování (hraní šachů, řízení autonomních vozidel) a predikci struktury či budoucího vývoje (predikce 3D struktury proteinů, odhadování vývoje cen akcií).

Pravděpodobnost umožňuje pracovat s nejistotou, která je ve strojovém učení nevyhnutelná, neboť model musí odhadovat odpovědi i pro nové příklady, které nikdy předtím neviděl.

Bayesova věta

Často umíme snadno určit P(B \mid A), kde A způsobuje nebo ovlivňuje B, ale zajímá nás opačná podmíněná pravděpodobnost P(A \mid B). Z posbíraných dat umíme snadno vypočítat pravděpodobnost, že e-mail obsahuje slovo „zázračný“, pokud jde o spam, ale pro klasifikaci e-mailů potřebujeme znát opačnou podmíněnou pravděpodobnost – pravděpodobnost, že jde o spam, když text obsahuje slovo „zázračný“. V takových případech lze podmíněnou pravděpodobnost „otočit“ podle Bayesovy věty:

P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}

Vzorec lze také vnímat jako update původní (nepodmíněné) pravděpodobnosti P(A) (prior) s přihlédnutím k nové informaci, že nastal jev B. Zpřesněná (podmíněná) pravděpodobnost P(A \mid B) se pak označuje jako posterior.

Pravděpodobnostní klasifikátor

Pravděpodobnostní modely lze nejsnáze využít pro řešení klasifikačních úloh (např. rozhodnout, zda je daný e-mail spam). Označme X příklad, který chceme klasifikovat, X_1, X_2, \ldots, X_n jeho jednotlivé atributy (např. přítomnost různých slov v textu e-mailu) a Y možné kategorie (spam / normální e-mail). Chceme predikovat kategorii s větší podmíněnou pravděpodobností P(Y \mid X). Tyto pravděpodobnosti můžeme spočítat s využitím Bayesovy věty:

P(Y \mid X) = P(X \mid Y) \cdot P(Y) \mathbin{/} P(X)

Zatímco určení P(Y) je snadné (spočítáme, jaký podíl e-mailů v trénovacích datech jsou spam), určení P(X \mid Y) vyžaduje exponenciálně mnoho příkladů vzhledem k počtu atributů (potřebovali bychom e-maily se všemi možnými kombinacemi uvažovaných slov). Možným řešením je pravděpodobnostní rozdělení odhadovat pouze přibližně pomocí nějakého modelu, který nemá exponenciální počet parametrů (např. neuronová síť).

Naivní Bayesův klasifikátor

Pro mnohé jednoduché problémy však stačí výrazně jednodušší řešení: předpokládat, že jednotlivé atributy jsou na sobě podmíněně nezávislé (při znalosti kategorie). Pak nám totiž stačí n jednoparametrických podmíněných pravědpodobností:

P(Y \mid X) = P(Y) \cdot P(X_1 \mid Y) \cdot P(X_2 \mid Y) \cdot \ldots \cdot P(X_n \mid Y) \mathbin{/} P(X)

Tento model se označuje jako Naivní Bayesův klasifikátor. Slovo „naivní“ se odkazuje právě na předpoklad podmíněné nezávislosti atributů, který typicky neplatí (např. přítomnost slova „zázračný“ zvyšuje pravděpodobnosti slova „lék“ i pokud víme, že jde o spam). Odhadnuté pravděpodobnosti tak můžou být hodně nepřesné. Pro úspěšnou klasifikaci však není podstatné, zda jsou pravděpodobnosti odhadnuté přesně, ale zda má skutečná kategorie nejvyšší odhadnutou pravděpodobnost, což často platí. Výhodou je nízký počet parametrů (lineární vzhledem k počtu atributů), nízký počet příkladů potřebných k učení a také rychlé učení (přímočarý výpočet hodnot parametrů).

Bayesovské sítě

Naivní Bayesův klasifikátor předpokládá, že jsou všechny atributy podmíněně nezávislé. V některých případech víme, že některé atributy nezávislé jsou a jiné nejsou. Takovou situaci můžeme modelovat pomocí Bayesovských sítí, což je orientovaný graf zachycující vztahy mezi pozorovanými a skrytými proměnnými (pozorované proměnné jsou na obrázcích níže podbarvené šedě):

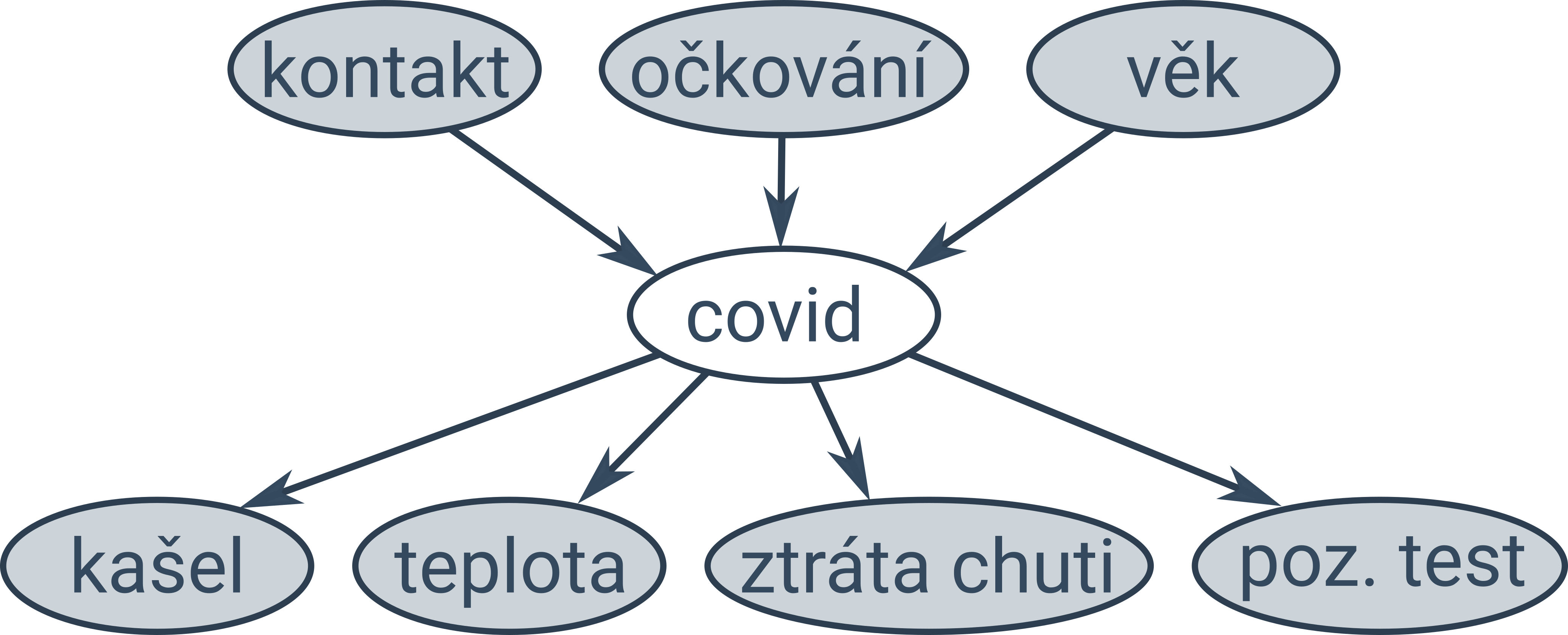
Naivní Bayesův klasifikátor je speciální typ Bayesovské sítě s následující jednoduchou strukturou:

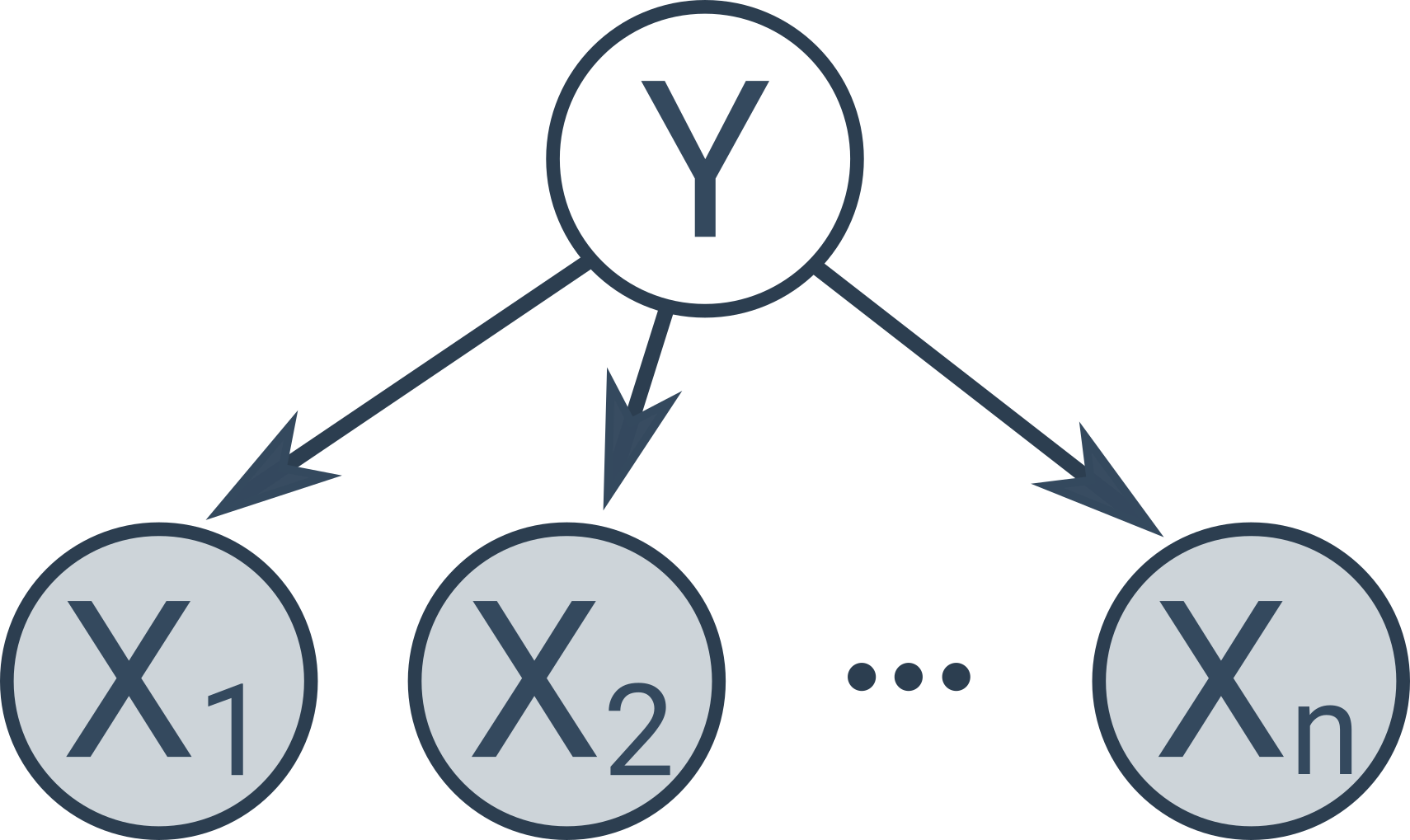
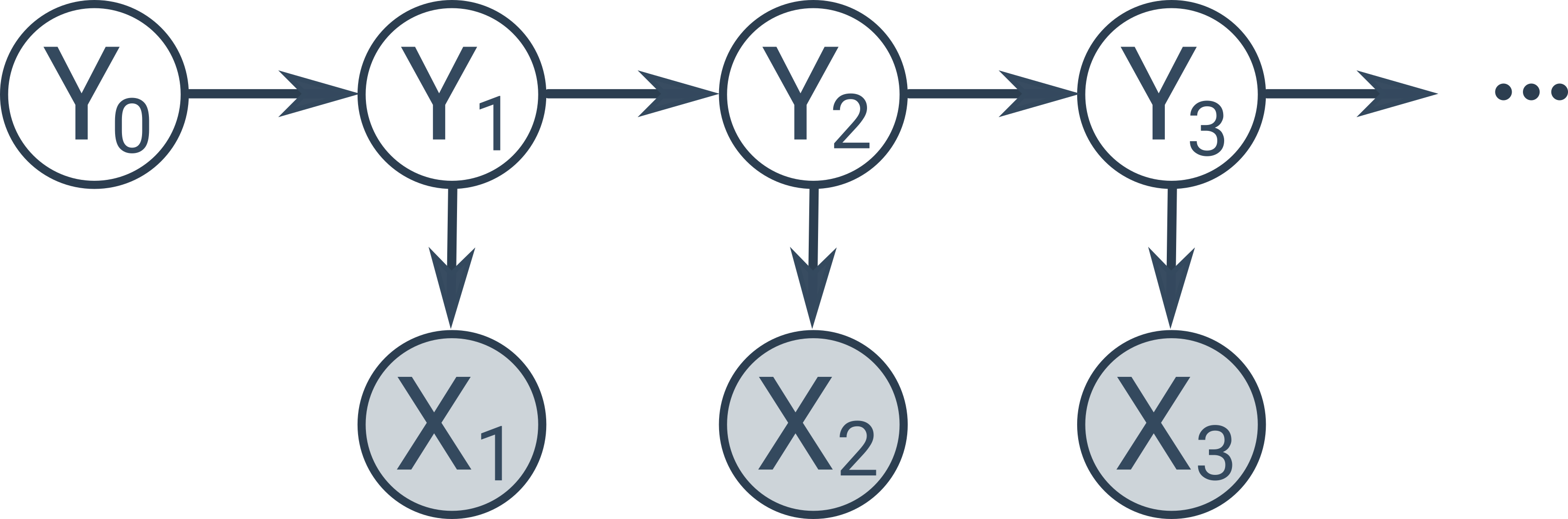
Existují další speciální typy Bayesovských sítí, např. skryté Markovovy modely, znázorňujı́cı́ časovou posloupnost skrytých stavů (poloha robota, vyslovovaný text), v nı́ž každý stav závisı́ pouze na jednom předchozı́m stavu a produkuje pozorovatelné měření (měření ultrazvukového senzoru, zaznamenaný zvuk).