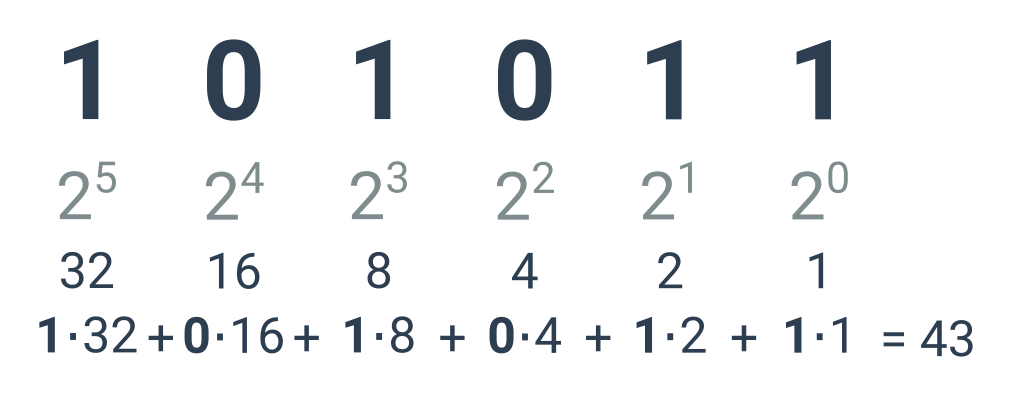Binární čísla: základy

Princip binární soustavy
V binární (dvojkové) soustavě zapisujeme čísla pouze pomocí dvou číslic: 0 a 1. Pozice každé číslice v zápisu odpovídá určité mocnině dvojky. Mocniny vždy začínají nultou mocninou u číslice nejvíc vpravo a zvyšují se směrem doleva. Hodnotu binárního čísla pak spočteme jako součet těchto mocnin. Každou mocninu započítáme, pokud je na příslušné pozici 1 nebo nezapočítáme, pokud je na daném místě 0.
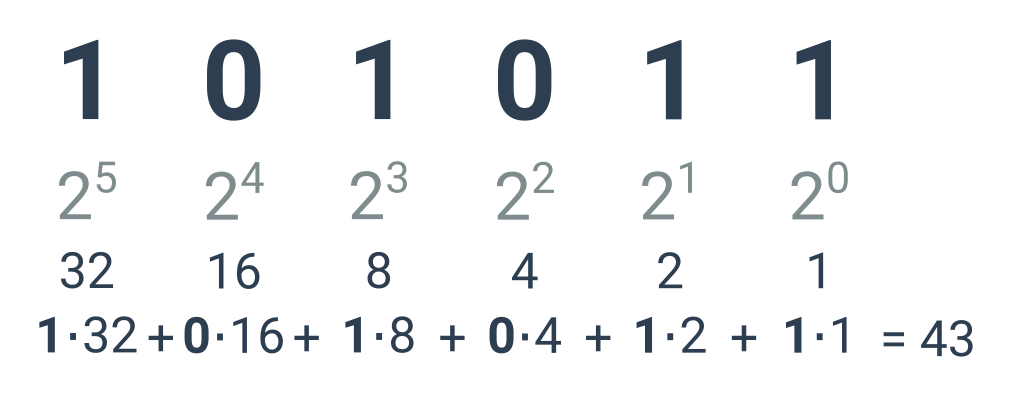
Značení soustav
Abychom odlišili, jestli mluvíme o čísle v binární nebo v desítkové soustavě, přidáváme k číslům dolní indexy značící soustavu. Například číslo 5 v desítkové soustavě budeme psát jako 5_{10}, binární číslo s hodnotou 5 napíšeme jako 101_2. Potom můžeme jasně rozlišit, že například zápisem 11_{10} myslíme desítkové číslo 11, zatímco zápis 11_2 budeme interpretovat jako binární číslo 11 a tedy desítkové číslo 3.
Intuitivní pomůcka
Pro základní představu o binárních číslech můžeme použít pomůcku, kterou máme vždy po ruce – totiž ruku samotnou. Představme si, že si na prsty ruky napíšeme mocniny dvojky:
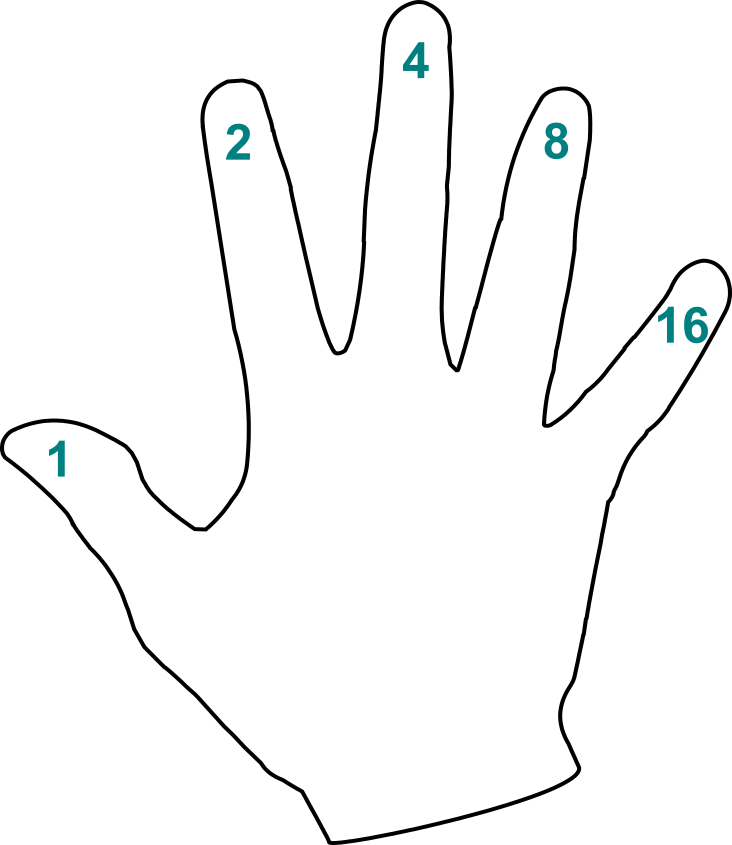
Pak můžeme na prstech jedné ruky počítat nejen do pěti, ale až do třiceti jedné. Každé číslo lze totiž vyjádřit (jednoznačně) jako součet mocnin dvojky. Pokud polohu prstů zaznačíme pomocí nul a jedniček, dostaneme zápis v binární soustavě.
Příklady čísel zapsaných v binární soustavě
| 1 |
1 |
1 |
| 2 |
2 |
10 |
| 3 |
2+1 |
11 |
| 4 |
4 |
100 |
| 5 |
4+1 |
101 |
| 6 |
4+2 |
110 |
| 7 |
4+2+1 |
111 |
| 8 |
8 |
1000 |
| 9 |
8+1 |
1001 |
| 10 |
8+2 |
1010 |
| 16 |
16 |
10000 |
| 20 |
16+4 |
10100 |
| 30 |
16+8+4+2 |
11110 |
Zavřít