Rozhodovací strom (angl. decision tree) je model, který odhaduje výstup na základě podmínek nad vstupními atributy daného příkladu.
Určení predikce podle rozhodovacího stromu
Proces rozhodování lze zachytit diagramem ve tvaru stromu (typ grafu), jehož vnitřní uzly obsahují podmínky a listy (koncové uzly, které se již nevětví) obsahují predikce. První podmínka je v kořenovém uzlu a dále postupujeme po hranách (šipkách) do levého nebo pravého podstromu podle toho, zda podmínka pro daný příklad platí, nebo neplatí. Cestu z kořene do listu lze interpretovat jako složenou podmínku spojenou s jedním klasifikačním pravidlem. Nejpravější větev následujícího stromu zachycuje pravidlo: „Pokud má příšerka alespoň 4 ruce a alespoň 5 očí, tak je zlá.“.
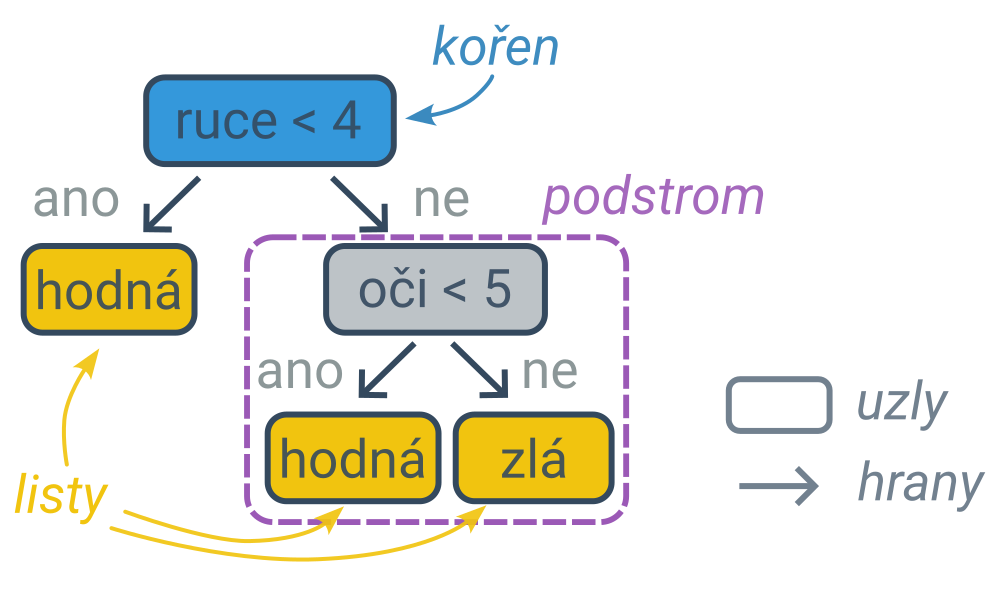
Rozhodovací stromy lze využít na řešení klasifikačních i regresních úloh. Klasifikační rozhodovací strom má v listech predikované kategorie, regresní rozhodovací strom predikované číselné hodnoty.
Učení rozhodovacích stromů
V případě klasifikačních úloh hledáme takový rozhodovací strom, který maximalizuje správnost (počet správně klasifikovaných případů, angl. accuracy) na zadané trénovací množině příkladů. Možných stromů je příliš mnoho na to, abychom mohli vyzkoušet všechny, proto strom tvoříme postupným přidáváním uzlů s podmínkami. (Tento přístup, kdy děláme lokálně optimální rozhodnutí, která však negarantují celkově optimální výsledek, se označuje jako hladový algoritmus.)
Začínáme s celým datasetem příkladů a hledáme podmínku, která rozdělí příklady na dvě co nejhomogenější skupiny. (Ideální podmínka by platila pro všechny příklady jedné kategorie a neplatila pro všechny příklady druhé kategorie – pak bychom totiž dosáhli nejvyšší možné správnosti predikcí.) Míru nehomogenity lze kvantifikovat například pomocí entropie nebo Gini indexu, což jsou podobné funkce, které jsou nulové pro zcela homogenní rozdělení a nejvyšší hodnotu mají pro rovnoměrné rozdělení (půlka příkladů z první kategorie, půlka příkladů z druhé kategorie).
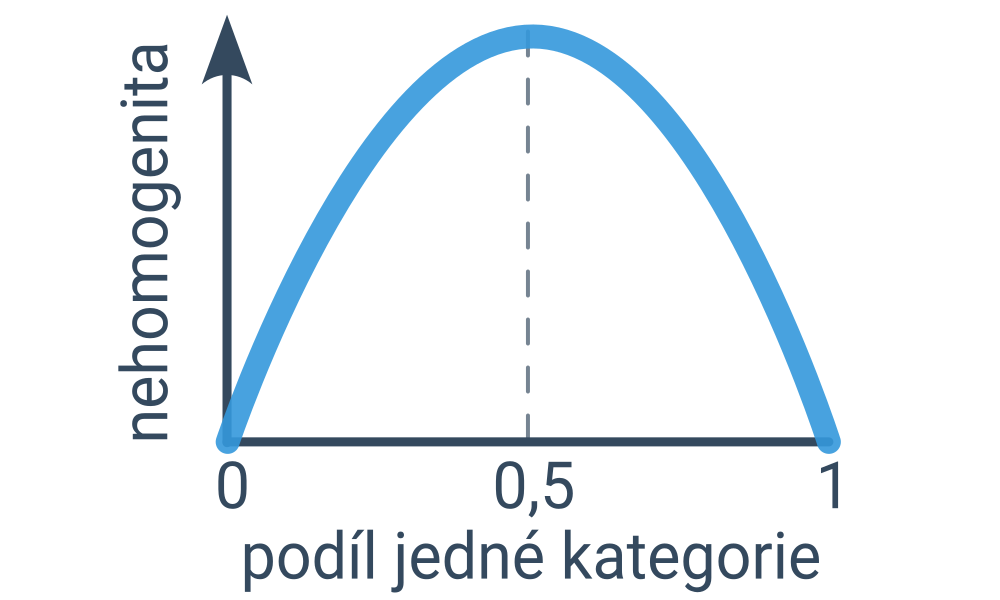
Vybraná nejlepší podmínka se stává kořenem stromu. Stejný proces pak opakujeme pro každý podstrom, dokud dochází k zvyšování homogenity, dokud máme v uzlu dostatek příkladů a/nebo dokud strom není příliš hluboký. Predikce potom odpovídá nejčastější kategorii příkladů, které prošly do tohoto listu. (V případě regresních rozhodovacích stromů by to byla průměrná hodnota příkladů.)
Výhody a nevýhody rozhodovacích stromů
Rozhodovací stromy jsou jednoduché a velmi dobře interpretovatelné. Stromy lze přirozeně vizualizovat a pro jednotlivé predikce lze generovat jasná vysvětlení – složené podmínky dané cestou z kořene do listu. Tyto podmínky jsou navíc nad původními atributy, neboť rozhodovací stromy nevyžadují normalizaci atributů (oproti např. lineárním modelům). Rozhodovací stromy umožňují zachytit nelineární interakce mezi atributy, naopak však nedokáží efektivně zachytit lineární vztahy (jen přibližně pomocí velkého množství podmínek).
Rozhodovací stromy jsou náchylné k přeučení, čemuž lze předejít omezením hloubky a prořezáváním větví, které příliš nepřispívají k celkové správnosti predikcí. I při těchto opatřeních jsou však stromy nestabilní – malá změna dat může výrazně ovlivnit výsledný strom. Nestabilní jsou i jednotlivé predikce – malá změna jednoho atributu může způsobit skokovou změnu predikované hodnoty.
Rozšíření rozhodovacích stromů
Složitější modely kombinují více rozhodovacích stromů do jednoho modelu, aby zvýšily kvalitu predikcí. Náhodný les (angl. random forest) je agregace velkého množství rozhodovacích stromů naučených na náhodných podmnožinách trénovacích dat, jejichž predikce se průměrují. To zvyšuje stabilitu predikcí a snižuje náchylnost k přeučení. Nevýhodou je výrazně horší interpretovatelnost.











