Odvozování logických důsledků z předpokladů je velmi důležitá dovednost. Nejde jen o samotné odvozování, ale i o schopnost rozpoznat, jestli nějaké tvrzení plyne z faktů, které známe.
V této sekci si ukážeme hned několik druhů odvozování.
Řetězení implikací
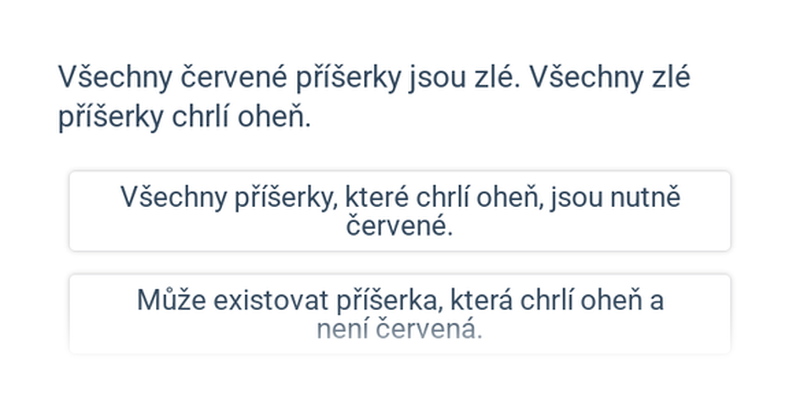
Kdykoli z prvního faktu plyne druhý, a z druhého plyne třetí, pak z prvního faktu bude plynout i fakt třetí.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Pokud jdeme plavat, pak prší.“ dokážeme vyvodit, že každé úterý prší.
- Z předpokladů „Všichni čerti mají rohy.“ a „Pokud má někdo rohy, pak má i ocas.“ můžeme vyvodit, že všichni čerti mají ocas.
- Z předpokladů „Všechno ze dřeva hoří.“ a „Všechny pochodně jsou ze dřeva.“ můžeme vyvodit, že všechny pochodně hoří.
Implikace s pravdivým předpokladem
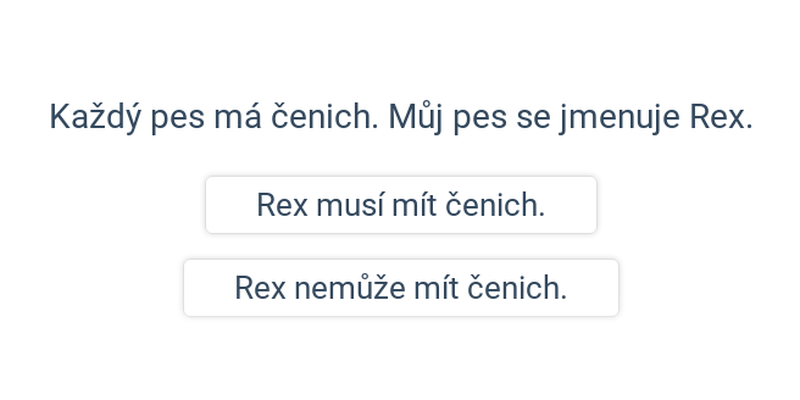
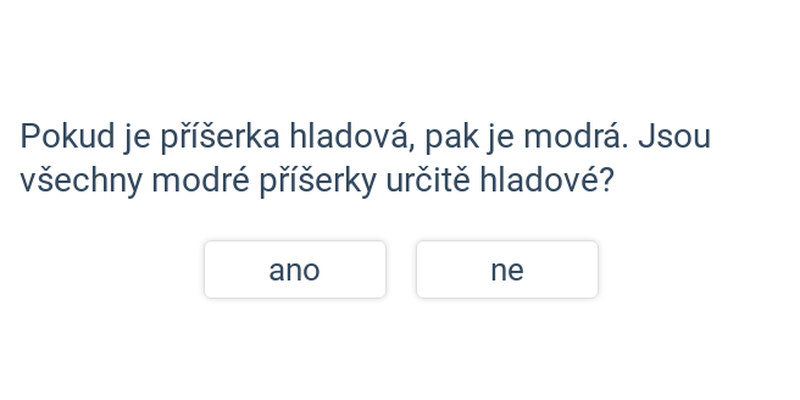
Pokud máme implikaci, která má platný předpoklad, pak nutně platí i její závěr.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Dnes je úterý.“ dokážeme vyvodit, že dnes jdeme plavat.
- Z předpokladů „Všichni čerti mají rohy.“ a „Jsem čert.“ můžeme vyvodit, že mám rohy.
Implikace s nepravdivým závěrem
Pokud máme implikaci, která má neplatný závěr, pak nutně nesmí platit její předpoklad. To je proto, že kdyby platil předpoklad, pak by musel platit i závěr, o kterém víme, že neplatí.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Dnes nejdeme plavat.“ dokážeme vyvodit, že dnes nemůže být úterý.
- Z předpokladů „Všichni čerti mají rohy.“ a „Nemám rohy.“ můžeme vyvodit, že nejsem čert.
Vyvozování z implikace a ekvivalence
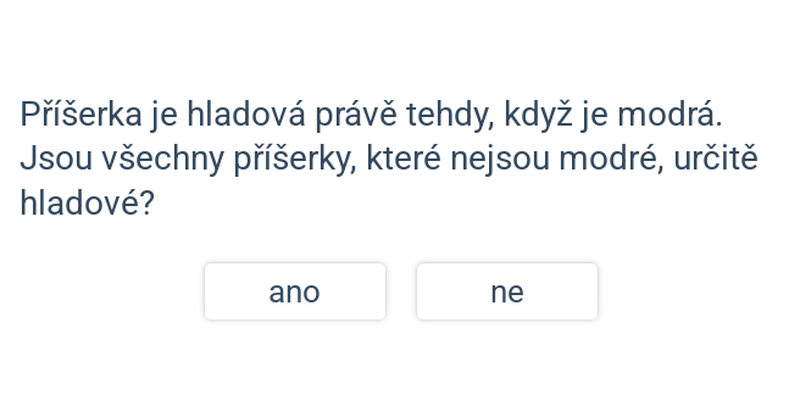
Při vyvozování závěrů z implikací a ekvivalencí můžeme postupovat více způsoby. Jednou z možností je si vzít hodnoty z vyvozovaného závěru a dosadit je do původní implikace či ekvivalence.
Příklad vyvozování dosazením
Mějme zadanou ekvivalenci „Autíčko je v šuplíku právě tehdy, když je zelené.“. Pak závěry „Všechna autíčka v šuplíku jsou zelená.“ a „Žádné červené autíčko není v šuplíku.“ jsou pravdivé, ale nemůžeme vyvodit „V šuplíku je červené autíčko.“ nebo „Alespoň jedno zelené autíčko je mimo šuplík.“. Proč? Ukažme si postup na prvním závěru („Všechna autíčka v šuplíku jsou zelená.“). Dosadíme si tedy do původní ekvivalence pravdu za „autíčko je v šuplíku“ a dostaneme „Pravda právě tehdy, když je autíčko zelené.“, což je totéž jako „Autíčko je zelené.“. Předpokládali jsme libovolné autíčko v šuplíku a dostali, že je zelené. Takže musí být pravda, že „Všechna autíčka v šuplíku jsou zelená.“.
Další možností je upravit si tvrzení na jiné ekvivalentní. K tomu mohou nejvíce pomoci pravidla v sekci úpravy logických výrazů, ale některá si ukážeme i tady. Všechna vyplývají z definic.
Úpravy implikace a ekvivalence
- Implikaci můžeme přepsat pomocí nebo. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat jako „Nebude svítit slunce nebo půjdu ven.“, nebo dlouze „Nebude svítit slunce, nebo bude svítit slunce a půjdu ven.“.
- Takzvaná obměna implikace je úprava implikace na jinou ekvivalentní implikaci. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat na „Pokud nepůjdu ven, pak nebude svítit slunce.“
- Ekvivalence se dá přepsat na dvě implikace takto: „Slunce bude svítit právě tehdy, když půjdu ven.“ můžeme přepsat na „Pokud bude svítit slunce, pak půjdu ven, a zároveň pokud půjdu ven, pak bude svítit slunce.“
- Ekvivalenci můžeme přepsat i na kombinaci „a zároveň“ a „nebo“. „Slunce bude svítit právě tehdy, když půjdu ven.“ pak bude „Bude svítit slunce a půjdu ven, nebo nebude svítit slunce a nepůjdu ven.“
Pokud preferujete grafické znázornění, můžete si implikace zobrazovat pomocí diagramů. Část u pokud vyznačíme jako menší kruh a část za pak jako větší okolo toho menšího.
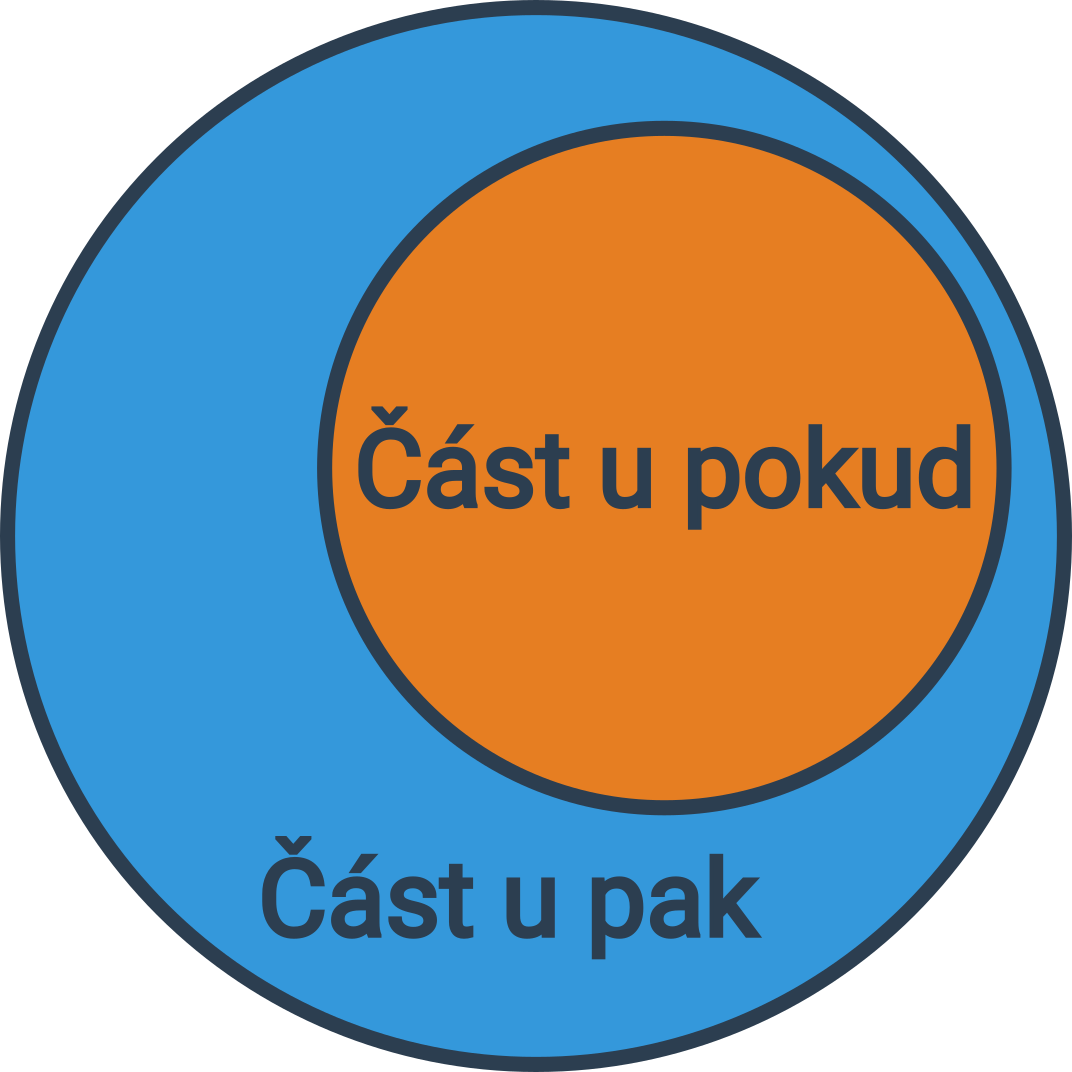
Diagramy
Mějme opět výrok „Pokud bude svítit slunce, pak půjdu ven.“ Výrok „bude svítit slunce“ vyznačíme jako menší kruh a výrok „půjdu ven“ jako větší okolo toho menšího.
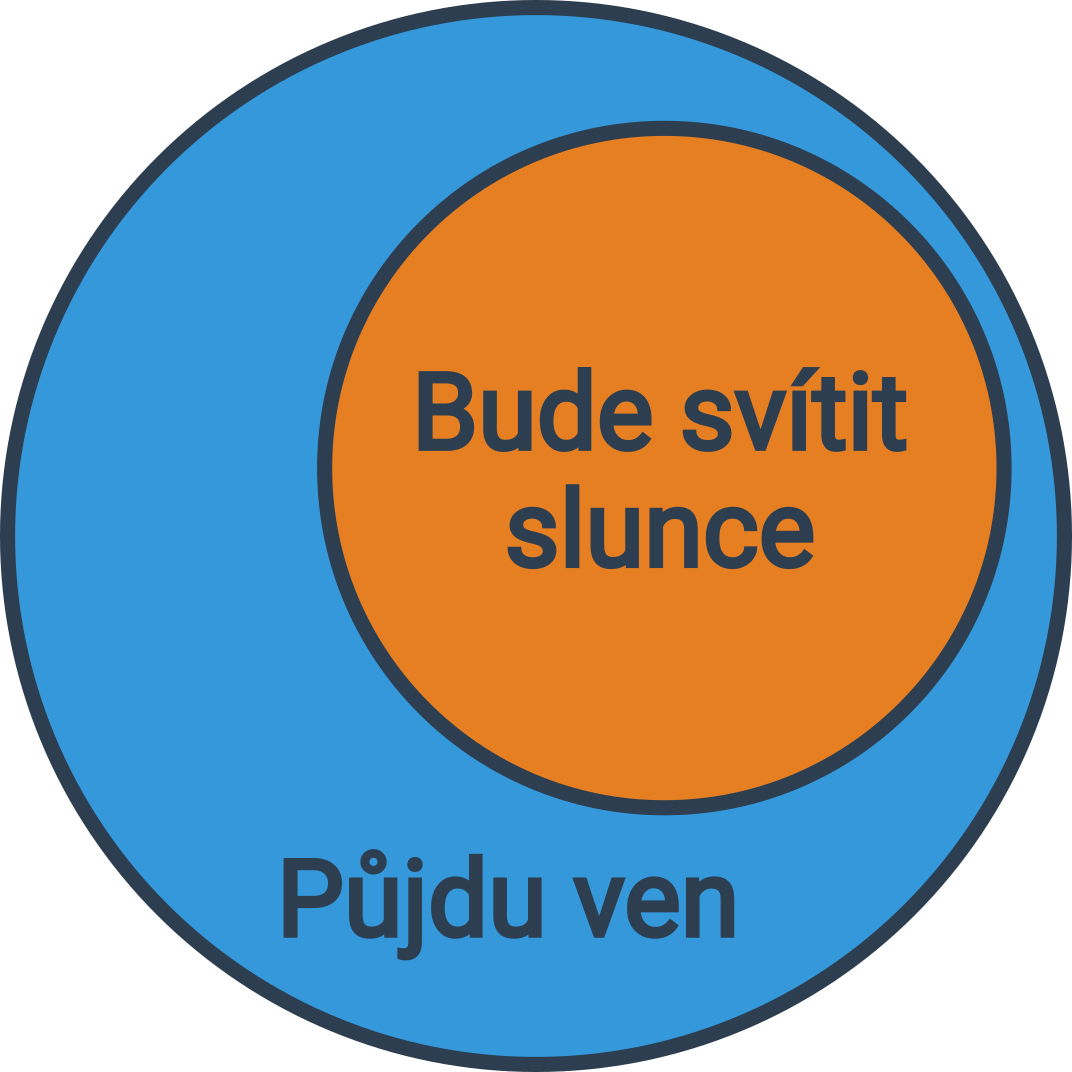
Při vyvozování závěrů se pak stačí podívat na obrázek a určit, kde se chtěná situace nachází.
Ukažme si to na příkladu. Ptáme se, jestli může nastat situace, kdy půjdu ven když nebude svítit slunce. To může nastat v místě diagramu, které je uvnitř modrého kruhu, ale je mimo oranžový kruh. Taková oblast na diagramu opravdu existuje, a proto může taková situace nastat.