Modelování pomocí grafů
MZBPojem „graf“ má bohužel v češtině několik odlišných významů. Mimo jiné používáme grafy funkcí, grafy pro vizualizaci dat a grafy modelující vztahy mezi objekty.
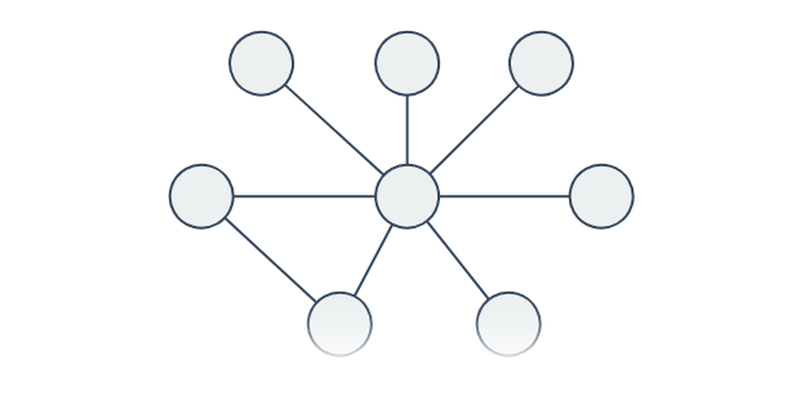
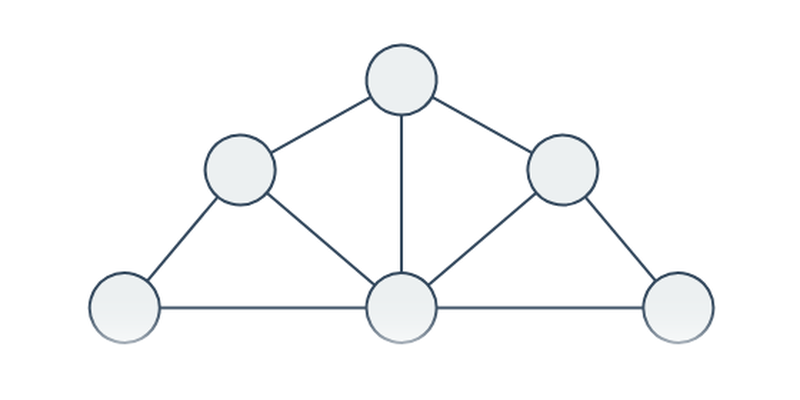
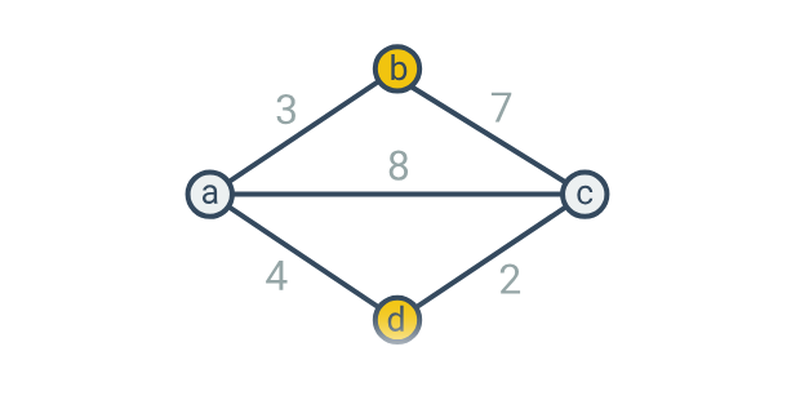
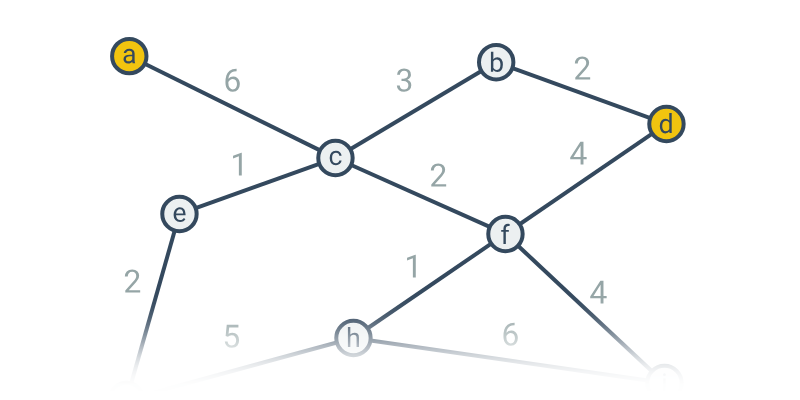
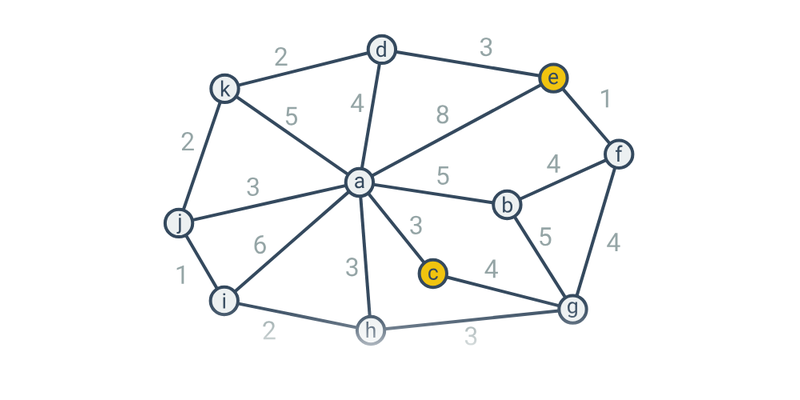
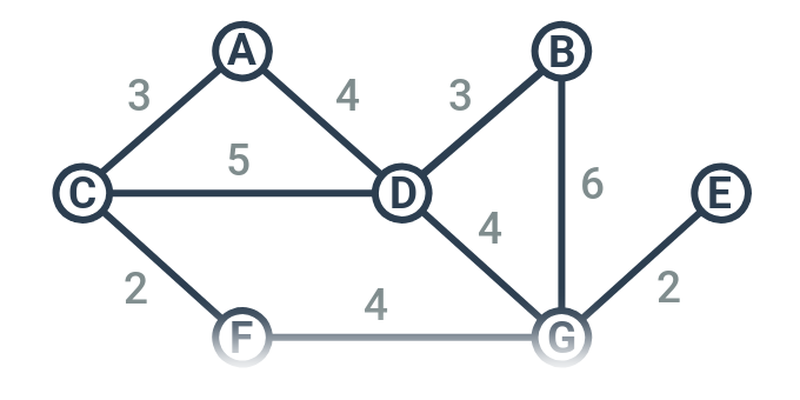
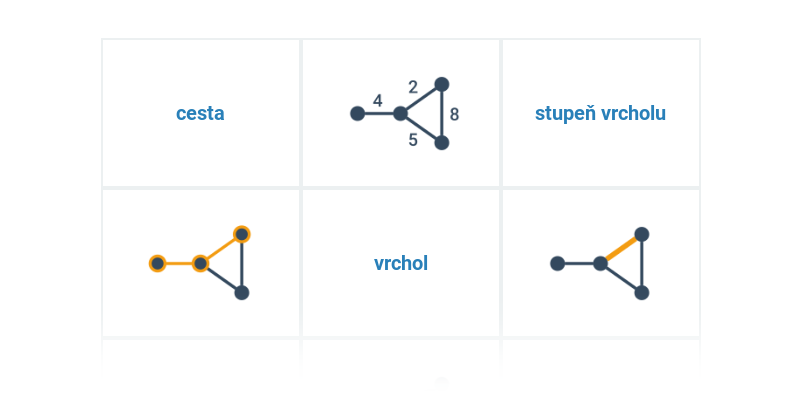
Zde se zabýváme posledním zmíněným významem. V tomto případě se grafem rozumí vrcholy („tečky“) a hrany („spojnice“). Takovéto grafy se používají pro modelování vztahů mezi objekty, například:
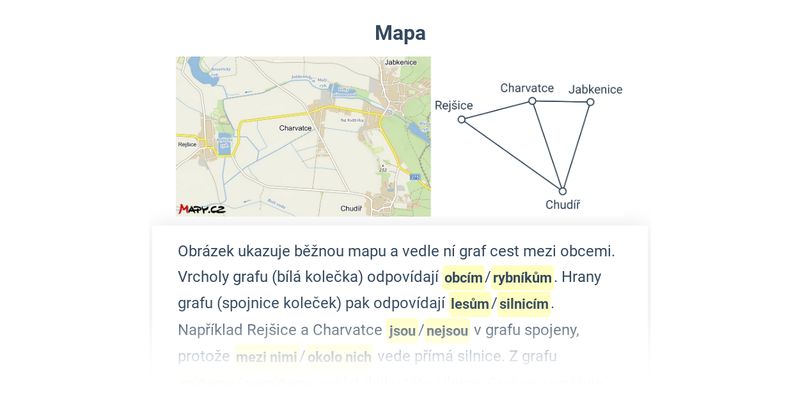
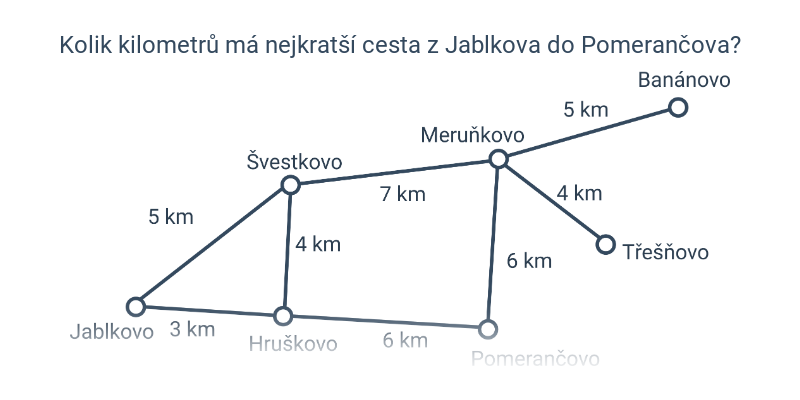
- Dopravní síť: vrcholy jsou města, hrany jsou silnice mezi nimi.
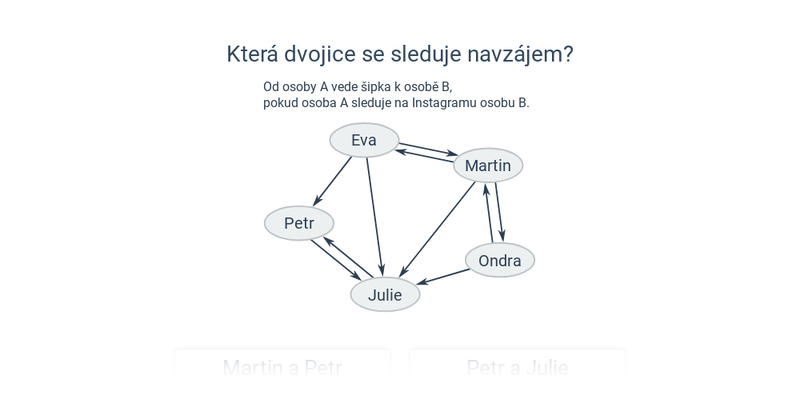
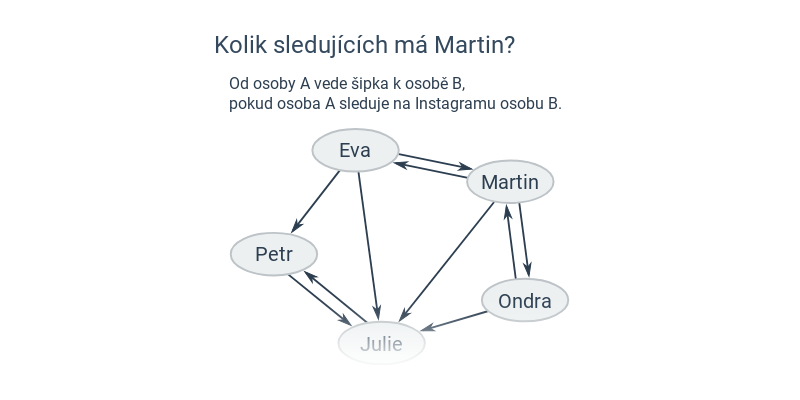
- Sociální síť: vrcholy jsou lidé, hrany odpovídají přátelství.
- Webové stránky: vrcholy jsou jednotlivé stránky, hrany odpovídají odkazům mezi nimi.
Základní témata o grafech se zaměřují na použití grafů na intuitivní úrovni (tato témata jsou vhodná i na úrovni základní školy):
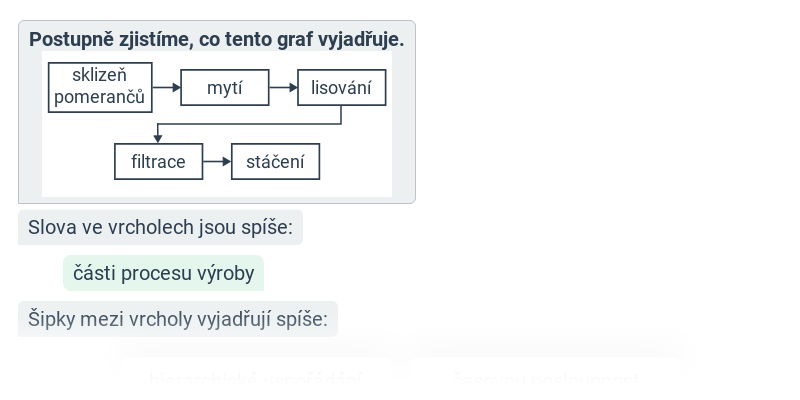
- Grafy a abstrakce – použití grafu jako modelu skutečnosti, porozumění významu grafů
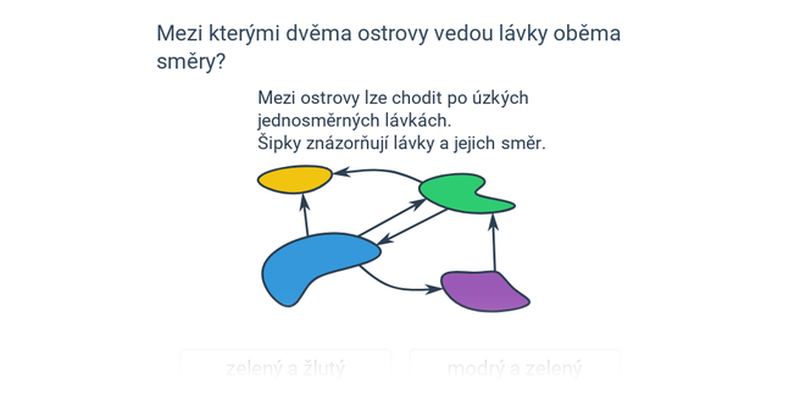
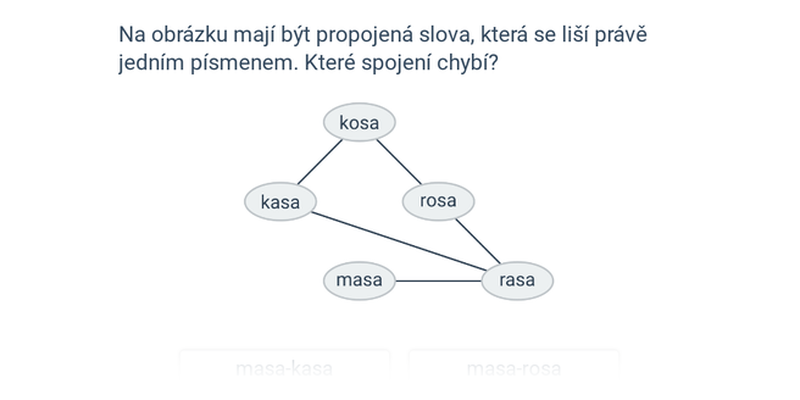
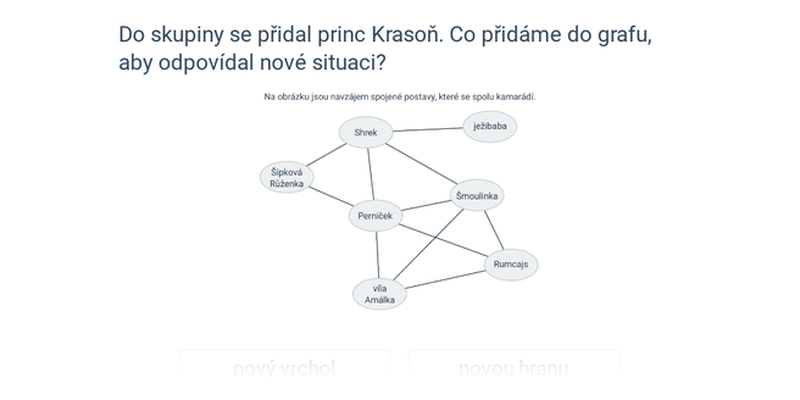
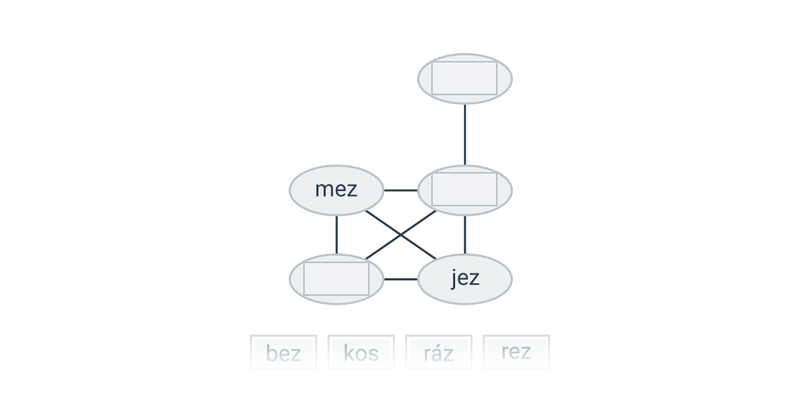
- Grafy sousednosti – jeden konkrétní případ užití grafů, na kterém se dá čistě obrázkovou formou dobře procvičit princip abstrakce
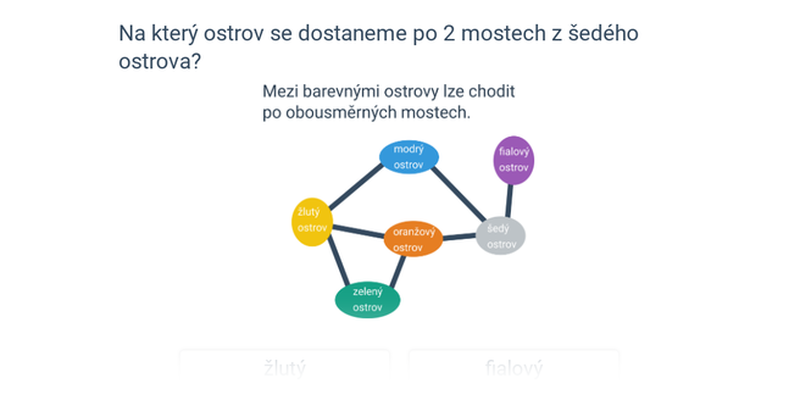
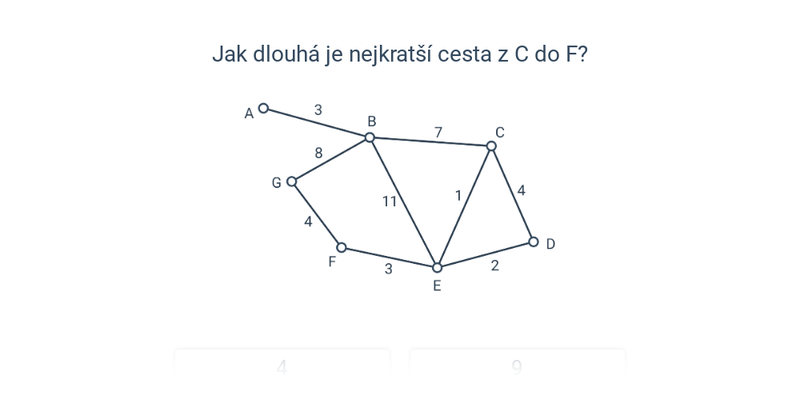
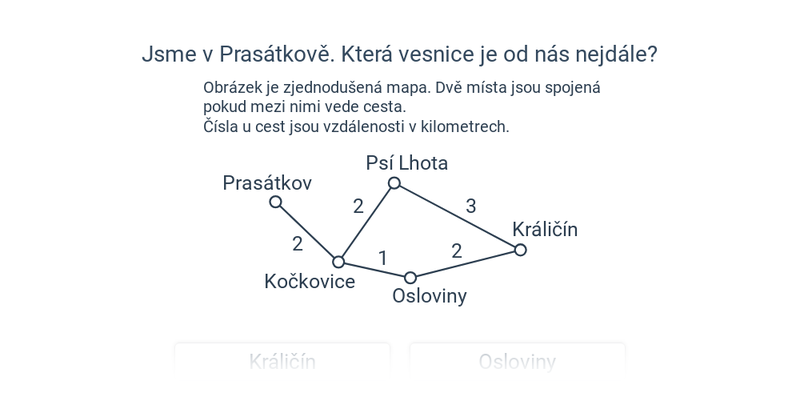
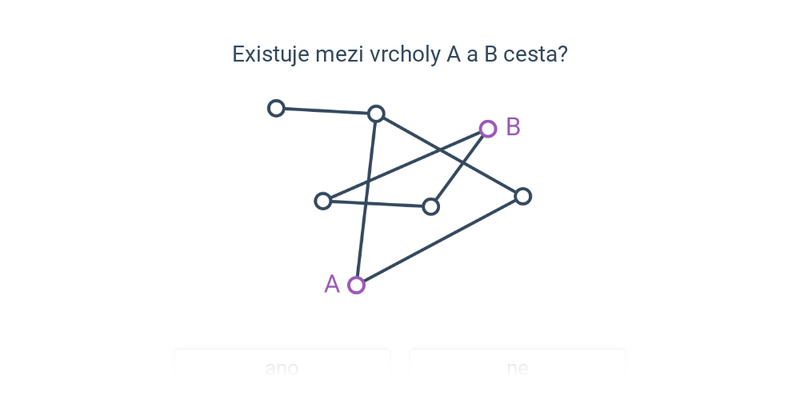
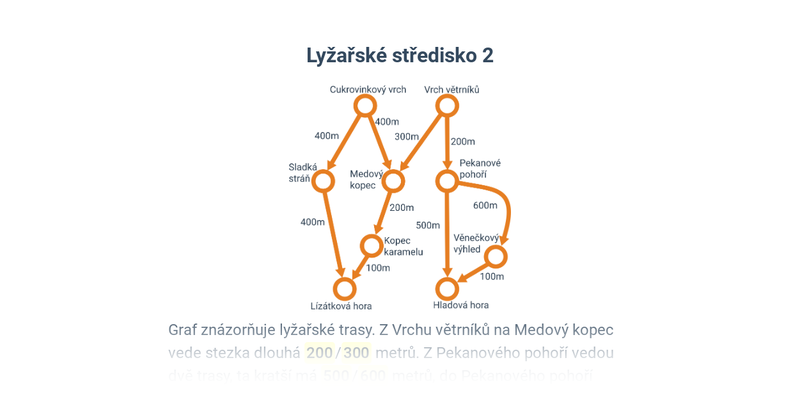
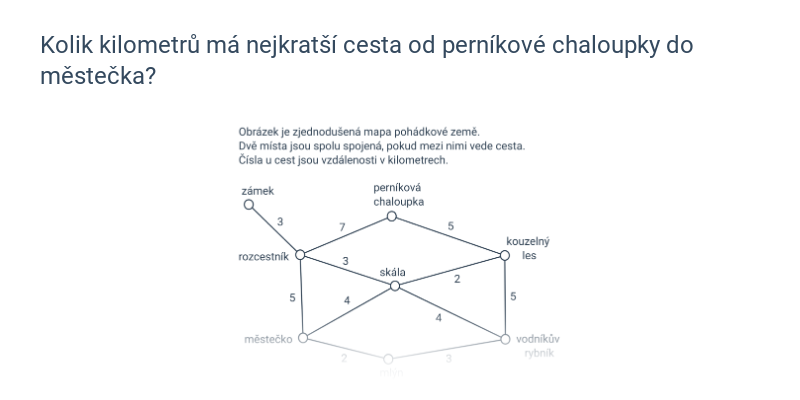
- Nejkratší cesty – intuitivní příklady na hledání nejkratších cest mezi vrcholy, což je jedna z typických aplikací grafů
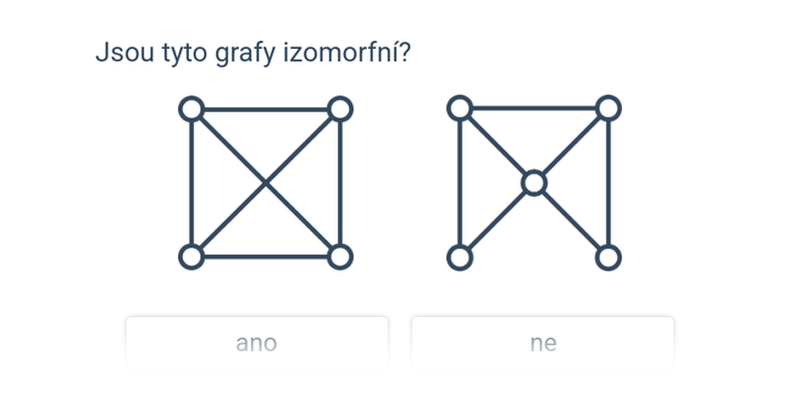
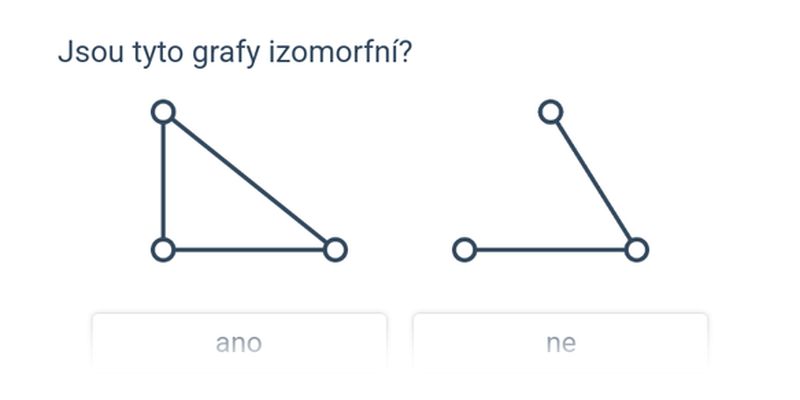
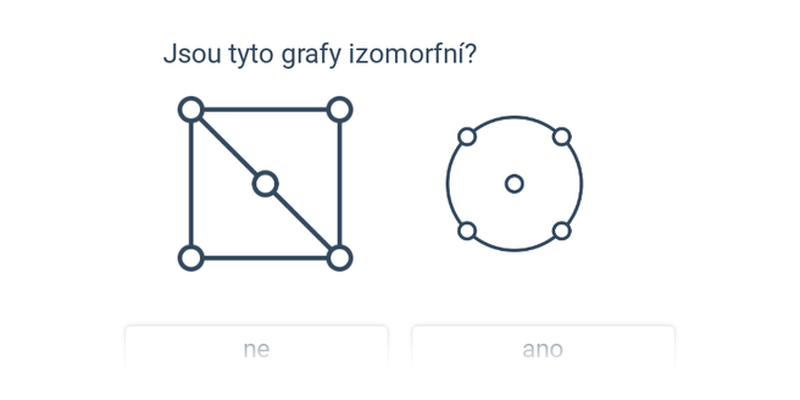
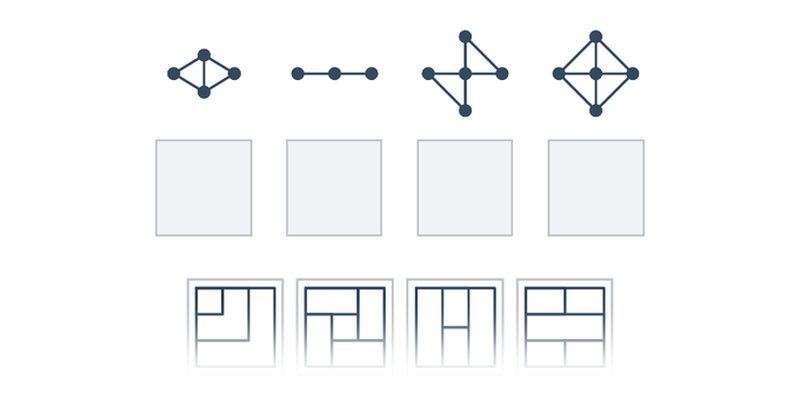
- Izomorfní grafy – téma se složitě znějícím názvem, ale poměrně intuitivními obrázkovými zadáními; hledáme grafy, které mají „stejná spojení“
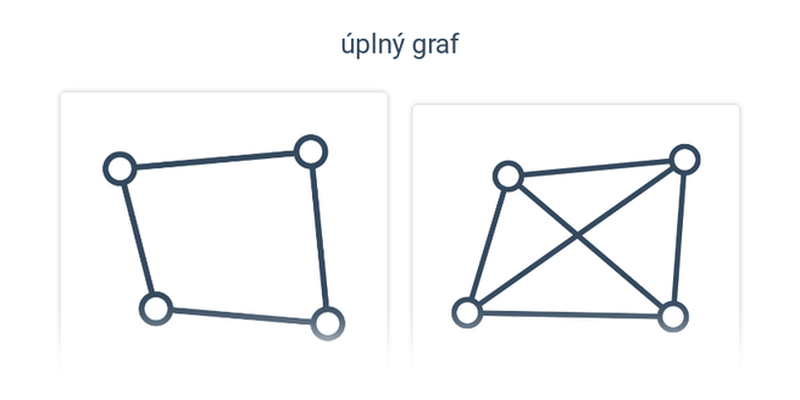
Grafy mají v informatice bohaté využití. Abychom mohli s grafy více pracovat, nevystačíme jen s obrázky, ale potřebujeme i přesně pracovat s pojmy. Tím se zabývá oblast zvaná teorie grafů. Toto důkladnější pojetí už je na úrovni střední a vysoké školy:
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.
Pexeso
Hledání dvojic, které k sobě patří.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Doplňování textu
Krátké texty, do kterých doplňujete na vybraná místa správnou variantu ze dvou možností.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.