Výpis souhrnů
Digitální technologie
Podtémata
- Digitální technologie
- Hardware
- Typy počítačů
- Historie počítačů
- Hardware: základy
- Vstupní a výstupní zařízení
- Procesor a architektura
- Paměť
- Software
- Software: typy aplikací, příklady
- Vlastnosti softwaru
- Typy souborů
- Organizace souborů
- Operační systémy
- Počítačové sítě
- Internet a web
- Počítačové sítě: obecné principy
- Počítačové sítě: protokoly
- Počítačové sítě: hardware
- Mobilní telefony
- Mobilní telefony: základy
- Mobilní telefony: software, připojení, platby
- Mobilní telefony: hardware
Digitální technologie
Digitální technologie představují širokou škálu elektronických zařízení a systémů, pomocí kterých můžeme komunikovat a zpracovávat informace. Toto téma nabízí přehled hlavních principů digitálních technologií rozdělený do několika podtémat:
- Hardware – fyzické součásti počítačů
- Software – programové vybavení počítačů
- Počítačové sítě – propojení počítačů do větších celků
- Mobilní telefony – běžně používané malé počítače
Aby technologie byly v našem životě přínosné, musíme nejen rozumět jejich principům, ale také je správně používat. Tomu se věnuje téma použití technologií.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 4.–6. ročník | základní znalosti a dovednosti týkající se počítačů a mobilních telefonů | |
| 7.–9. ročník | důraz na bezpečnostní rizika při použití digitálních technologií, preventivní opatření | |
| 8.–10. ročník | přehled technických základů digitálních technologií | |
| 10.–13. ročník | hlubší pokrytí témat určené pro žáky středních škol |
Hardware zahrnuje všechny fyzické součásti počítačů, jako jsou procesor, paměť, displej nebo klávesnice. Hardware představuje prvky počítače, na které si můžeme „sáhnout“. Oproti tomu software je nehmotný, označuje instrukce, které řídí hardware a umožňují uživatelům provádět různé úkoly. Hardware a software spolupracují, abychom mohli počítače používat, potřebujeme obojí.
Dílčí podtémata týkající se hardwaru jsou:
- Typy počítačů – Existuje řada různých typů počítačů a každý se hodí k jinému účelu.
- Historie počítačů – Povědomí o tom, jak se počítače vyvíjely, nám může pomoct lépe pochopit současné počítače a představit si, jaké by mohly být v budoucnosti.
- Hardware: základy – Představuje hlavní součásti počítačů a jejich funkce. Toto podtéma se hodí pro základní přehled o hardwaru.
- Vstupní a výstupní zařízení – Pomocí těchto zařízení s počítači komunikujeme, patří mezi ně klávesnice, myš, monitor, tiskárna nebo reproduktory.
- Procesor a architektura – Procesor je nejdůležitější součást počítače řídící ostatní hardwarové součásti.
- Paměť – Stejně jako lidé i počítače ukládají informace do paměti, počítačových pamětí však existuje více druhů a každá se hodí k něčemu jinému.
Další hardwarové součástky se používají v počítačových sítích.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 4.–6. ročník | modul obsahuje mj. základní pojmy o hardwaru | |
| 8.–10. ročník | přehled pojmů, porozumění základním principům, souvislosti se softwarem | |
| 10.–13. ročník | hlubší pokrytí určené pro žáky středních škol |
Typy počítačů
Počítače se ve světě vyskytují v mnoha formách.
V domácnostech a kancelářích se často setkáme s PC (personal computer, osobní počítač). Nepřenosnému PC se říká stolní počítač, někdy také desktop. Stolní počítač se obvykle skládá z počítačové skříně, ke které připojujeme příslušenství jako monitor, klávesnici, reproduktory apod. Počítačová skříň, která se staví na výšku a často pod stůl, se nazývá tower. Existují i kompaktnější verze stolních počítačů — například all-in-one PC, kde je všechen hardware vestavěný přímo v monitoru.



Přenosnému osobnímu počítači se říká notebook. Ten má všechen hardware i příslušenství vestavěné přímo do svého těla. Přenosné počítače mívají navíc akumulátor (baterii), abychom je mohli používat, i když nejsou připojené do elektrické sítě. Smartphony (chytré telefony) a tablety jsou také přenosné počítače. Mívají dotykovou obrazovku a jsou poměrně malé. Ještě menší než smartphony jsou chytré hodinky (smartwatch), které si můžeme připnout na zápěstí a například propojit s chytrým telefonem pro pohodlnější ovládání.



Mainframe je velký a velmi výkonný počítač, který často používají firmy pro výpočetně náročné operace. Superpočítače jsou mnohonásobně výkonnější než osobní počítače i mainframy, mohou zabírat celé haly a většinou provádějí náročné vědecké výpočty. Server je počítač, který je připojený k počítačové síti (obvykle k internetu) a poskytuje služby jiným počítačům, které si je vyžádají. Například může zobrazovat webové stránky nebo poskytovat internetové úložiště.


Mnoho zařízení je dnes také ovládáno počítači. Těmto počítačům se říká vestavěné systémy a obvykle jsou zkonstruované přímo pro ovládání daného zařízení a vestavěné uvnitř. Nachází se například v moderních autech, letadlech, chytrých spotřebičích apod. Na výrobních linkách se používají CNC stroje (computer numerical control), které řídí počítač podle nějakého počítačového programu. Pomáhají zautomatizovat (a tedy zefektivnit) výrobu.
NahoruHistorie počítačů
V dávné historii si lidé ulehčovali počítání například s kuličkovými počítadly (abakus) nebo logaritmickými pravítky. První programovatelný stroj navrhl Charles Babbage v 19. století.


Za druhé světové války byl počítač použit k rozluštění německé šifry Enigma. Na tom se podílel i Alan Turing, který později vymyslel teoretický model počítače. Prakticky využívanou architekturu počítače (po svém autorovi nazývanou von Neumannova), která je používaná dodnes, navrhl John von Neumann.
Vývoj počítačů se často rozděluje do tzv. generací — vývojových fází, které se odlišují součástkami, ze kterých byly počítače složené, jejich rychlostí i použitím.
| Generace | Období | Zásadní technologie | Operace za sekundu |
|---|---|---|---|
| 1. | 40. léta 20. stol. | elektronky | stovky až tisíce |
| 2. | 50. – 60. léta 20. stol. | tranzistory | tisíce |
| 3. | 60. – 70. léta 20. stol. | integrované obvody | desetitisíce |
| 4. | 80. léta 20. stol. – nyní | integrované obvody | miliony a víc |
V 1. generaci velkou část funkčnosti počítače zajišťovaly elektronky. V té době byly počítače pomalé a poruchové, zabíraly velký prostor (typicky celé místnosti) a pro svůj běh vyžadovaly značné množství energie. Nejznámějším zástupcem této generace je počítač ENIAC, který byl postaven ve 40. letech 20. stol. v USA. Na světě bylo tehdy jen velmi málo počítačů, proto se používaly převážně pro náročné matematické výpočty pro armádu nebo pro výzkum. Informace jim byly předávány na děrných štítcích a děrných páskách.



Ve 2. generaci se objevily tranzistory, polovodičové součástky, které v počítačích nahradily elektronky a umožnily tak zvýšení spolehlivosti a rychlosti, zatímco snížily poruchovost. V 60. letech 20. stol. se začaly objevovat sálové počítače, které používaly například firmy pro vedení účetnictví nebo pro matematické výpočty.
Ve 3. generaci se díky integrovaným obvodům začaly počítače zmenšovat a zvyšovat svůj výkon. Integrovaný obvod sdružuje dohromady mnoho tranzistorů. Počítače se běžně nacházely ve výpočetních střediscích, kde bylo možné pronajmout si počítačový čas.
Ve 4. generaci vznikly mikroprocesory, procesory tvořené jediným integrovaným obvodem, které umožnily počítače ještě více zmenšit. Objevily se osobní počítače s grafickým rozhraním a počítače se tak mohly rozšířit i do domácností. Počátky internetu sice sahají až do 50. let 20. století, koncem 80. let 20. století se k němu však připojovalo více a více počítačů a vznikaly první webové stránky. Nejen díky internetu a pokračujícímu zmenšování cen i velikostí počítačů se počítače více a více objevovaly v běžném životě. Možnosti jejich využití se rozšířily z čistě matematických výpočtů až do širokého spektra, které známe dnes.



Hardware: základy
Hardware jsou hmotné (fyzické) součásti počítače. Z hardwaru sestávají jak stolní počítače, tak notebooky, smartphony aj. K fungování počítače je nutná spolupráce hardwaru a softwaru (např. operačního systému, aplikací).
Procesor
Procesor (CPU = central processing unit) je základní součástí počítače, která provádí výpočty a logické operace. Současné procesory bývají typicky vícejádrové, více čipů (fyzických jader) může zpracovávat více procesů současně. Významnou vlastností procesoru je taktovací frekvence. Souvisí s jeho výkonem (rychlostí), udává se v GHz (gigahertzech, 1 GHz = 1000 MHz).
Operační paměť
Operační paměť (RAM = random access memory) slouží k dočasnému ukládání dat, s nimiž počítač momentálně pracuje (data operačního systému a aplikací). Po vypnutí počítače se její obsah vymaže. Kapacita operační paměti se běžně udává v gigabajtech (GB, 1 GB = 1000 MB). Běžná kapacita operační paměti v současných zařízeních se pohybuje v řádu jednotek až desítek GB.
Úložiště
Úložiště slouží k dlouhodobému ukládání dat (např. fotografií, videí, dokumentů, operačního systému, aplikací…). Jeho kapacita obvykle bývá v řádu stovek GB až jednotek TB. Kapacita úložiště je typicky větší než kapacita operační paměti.
Na polovodičích je založena tzv. flash paměť. Tu využívá např. SSD (solid state drive, polovodičový disk), eMMC v mobilních zařízeních či paměťové karty (např. SD).
HDD (hard disk drive, pevný disk) využívá kovové plotny, na které se ukládají data na principu magnetismu. Obsahuje pohyblivé části, je pomalejší než SSD. Někdy se využívá ve stolních počítačích, z hlediska ceny za určitou kapacitu je výhodnější než SSD.
Zdroj, základní deska
Elektrické napětí potřebné pro provoz počítače poskytuje zdroj. U mobilních zařízení je přítomen akumulátor, který lze opakovaně nabíjet. Základní deska propojuje všechny součásti počítače.
Vstupní a výstupní zařízení
Vstupní zařízení zajišťují vstup dat do počítače (typicky od uživatele, případně z prostředí). Patří mezi ně např. myš (data o pohybu), klávesnice (data o stisknutých klávesách), skener (obraz) či mikrofon (zvuk).
Výstupní zařízení mají na starost výstup dat z počítače k uživateli. Mezi výstupní zařízení náleží např. displej, tiskárna (výstupem je obraz), reproduktory (výstupem je zvuk) nebo vibrační jednotka telefonu.
Vstupní a výstupní zařízení mohou být kombinovaná: např. tiskárna (výstupní) se skenerem (vstupní) či dotykový displej (výstupem je obraz, vstupem jsou dotyky). Zařízení „zvnějšku“ připojovaná k počítači se označují jako periferie.
Komunikační rozhraní a porty
Široce využívaným komunikačním rozhraním je USB (universal serial bus). Může přenášet různé typy dat, lze jím např. i nabíjet mobilní zařízení. USB využívá hlavně koncovky USB-A a USB-C (to lze zapojovat libovolnou stranou).
K přenosu obrazu a zvuku (tedy typicky připojení displejů, projektorů) slouží porty HDMI či DisplayPort.
Tipy k procvičování
Toto téma poskytuje přehled nejzákladnějších informací spojených s hardwarem. Procvičování a informace podrobněji zaměřené na konkrétnější oblasti najdete v podtématech:
Vstupní a výstupní zařízení
Vstupní zařízení
Vstupní zařízení je hardware, pomocí kterého počítač přijímá data (typicky od uživatele či z prostředí). Mezi vstupní zařízení patří např. klávesnice (snímá stisky kláves), myš (snímá pohyb), skener (snímá obraz) či mikrofon (zaznamenává zvuk). Vstup dat do počítače zajišťuje např. i snímání dotyků v rámci dotykového displeje.
Další příklady vstupních zařízení
- joystick
- touchpad
- fotoaparát/kamera
- akcelerometr
- GPS
Výstupní zařízení
Výstupní zařízení je hardware, do kterého počítač zapisuje či zobrazuje data (typicky je zpřístupňuje uživateli). Mezi výstupní zařízení patří např. displej (zobrazuje obraz), tiskárna (zajišťuje výstup grafických dat) nebo reproduktory (zajišťují výstup zvuku).
Další příklady výstupních zařízení
- dataprojektor
- sluchátka
- plotter
Typy tiskáren
Jehličková tiskárna k tisku používá tiskovou hlavu s malými jehličkami, které přes barvicí pásku otiskuje na papír. Je levná na pořízení i na provoz, ale tiskne pomalu a nekvalitně. Využívá se například pro označování jízdenek v hromadné dopravě.
Inkoustová tiskárna tiskne pomocí vystřelování miniaturních inkoustových kapek na papír. Její pořizovací cena je nízká a tiskne kvalitně, i když ne příliš rychle. Inkoustové náplně, nazývané cartridge, jsou však poměrně drahé, takže provoz tiskárny může být nákladnější. Často se používá v domácnostech nebo v menších kancelářích.
Laserová tiskárna kreslí obraz laserem na světlocitlivý válec. Na něj se poté nanese barva, která zůstane pouze na laserem ozářených místech, a válec se následně otiskne na papír. Je drahá na koupi, ale provoz na rozdíl od inkoustové tiskárny nákladný není. Tiskne velmi rychle a kvalitně, proto je dobře využitelná na místech, kde se tisknou velké objemy stránek – například v kancelářích. Barva používaná v laserových tiskárnách se nazývá toner.
Komunikační rozhraní (porty)
Vstupní a výstupní zařízení lze k počítači připojit přes komunikační rozhraní, kterým se také říká porty. Často se setkáme s následujícími typy:
- USB je nyní pravděpodobně nejčastěji používané komunikační rozhraní. Je velmi univerzální, je možné přes něj připojit například klávesnici, myš, tiskárnu, fotoaparát nebo paměťové zařízení. Také se používá k nabíjení mobilních zařízení.
- HDMI umí přenášet digitální obrazový a zvukový signál. Připojuje se přes něj monitor, televize, nebo jiné obrazové zařízení.
Starší porty
- PS/2 se v minulosti používal k připojení klávesnice a myši, nyní je nahrazen USB.
- VGA přenáší obraz, ale na rozdíl od HDMI analogově. V současnosti se už příliš nepoužívá.
Procesor a architektura
Důležité součásti počítačové architektury jsou:
CPU (central processing unit) – centrální procesorová jednotka. Nazývá se také procesor. Umí zpracovávat základní strojové instrukce, ze kterých lze složit veškerou funkčnost, kterou potřebují počítačové programy k fungování. V podstatě se tak stará o celkový chod počítače. Součásti procesoru jsou aritmeticko-logická jednotka, řadič a registry. Rychlost procesoru určuje mimo jiné taktovací frekvence, která udává, kolik operací procesor udělá za sekundu. Frekvence se udává v jednotkách GHz (gigahertz). V současnosti je zrychlování CPU složité, takže se většího výkonu dosahuje použitím více procesorových jader v jednom pouzdře. Tyto procesory se nazývají vícejádrové a jsou efektivní, protože dokáží zpracovávat více procesů najednou – paralelně.
GPU (graphics processing unit) – grafický procesor. Grafický procesor je součást grafické karty. Ta přijímá data o tom, co je potřeba zobrazit na monitoru, a převádí je na obrazový výstup pro monitor. Grafický procesor provádí rychlé výpočty, které jsou pro převod dat na obraz potřeba. Grafická karta může být integrovaná nebo dedikovaná. Integrovaná karta je typicky vestavěná součást CPU, je to méně výkonná, ale levnější možnost. Dedikovaná karta se často dodává odděleně, je dražší, ale výkonnější – je potřeba například pro moderní počítačové hry se složitou grafikou.
ALU (arithmetic logic unit) – aritmeticko-logická jednotka. Je to součást procesoru, která provádí aritmetické a logické operace.
Registry jsou velmi malá a velmi rychlá paměťová úložiště v procesoru. Procesor si v nich udržuje data, která právě zpracovává.
Sběrnice zajišťuje přenos dat. Sběrnic je mnoho typů. Můžou přenášet data jak uvnitř počítače (např. do grafické karty), tak mezi zařízeními (např. USB je také typ sběrnice).
Cache je velmi rychlá, ale poměrně malá paměť, která pomáhá zrychlovat běh počítače. Protože procesor je velmi rychlý v porovnání s pamětí, pokaždé, když si potřebuje načíst nějaká data z paměti, musí dlouho čekat. Aby se chod počítače tolik nezpomaloval, procesor si do cache ukládá často používaná data, která odtud může načíst rychleji. Cache je rychlejší než operační paměť, ale přesto nestačí na procesor a registry, takže k nějakému zpomalení stále dochází.
Síťová karta zprostředkovává komunikaci počítače s počítačovou sítí – např. s internetem.
Zvuková karta zajišťuje vstup a výstup zvukových dat z a do počítače.
Procesor při své práci komunikuje s různými typy paměti.
NahoruStejně jako lidská paměť i ta počítačová slouží k uchování informací. Pro různé účely se používají různé typy pamětí, které můžeme označovat podle účelu nebo technologie.
Dlouhodobá paměť slouží k dlouhodobému uložení dat – například fotografií, filmů nebo zdrojových kódů počítačových programů. Je to to úložiště, ke kterému máme přístup v Průzkumníku souborů. Data se v ní udrží nezávisle na tom, jestli je připojená k elektřině.
V operační paměti si počítač ukládá data a stavy procesů, se kterými právě pracuje. Je mnohem rychlejší než dlouhodobá paměť, takže pro urychlení běhu počítače se data z dlouhodobé paměti dočasně nahrávají do operační paměti, když je s nimi potřeba pracovat. Jako uživatelé k ní nemáme přímý přístup, pracuje s ní pouze procesor. Často se realizuje jako paměť typu RAM, takže po odpojení elektrického proudu se z ní všechna data vymažou.
Cache paměť je velmi rychlá, ale poměrně malá paměť, která pomáhá zrychlovat běh počítače. Protože procesor je velmi rychlý v porovnání s operační pamětí, pokaždé, když si potřebuje načíst nějaká data z paměti, musí dlouho čekat. Aby se chod počítače tolik nezpomaloval, procesor si do cache ukládá často používaná data, která odtud může načíst rychleji. Cache je rychlejší než operační paměť, ale na procesor a registry nestačí. Říká se jí také vyrovnávací paměť nebo mezipaměť.
RAM (random access memory) umožňuje rychlý zápis i čtení, a proto se používá jako krátkodobá (například operační) paměť. Její název znamená, že v ní lze přistoupit okamžitě na libovolnou adresu. Ke svému fungování potřebuje elektrický proud, po jeho odpojení všechna data z paměti zmizí.
ROM (read only memory) česky znamená paměť pouze pro čtení, tedy do ní není možné data zapisovat, ale pouze je číst. Používá se jako dlouhodobé úložiště, data v ní zůstanou i po odpojení elektrického proudu.
Flash paměť je podtyp ROM, který ale lze přepisovat – jde do ní tedy na rozdíl od klasické ROM ukládat nová data. Zápis i čtení probíhá pomocí elektrického proudu. V současnosti je to velmi rozšířený typ dlouhodobého úložiště, používá se například v SSD, flash discích nebo paměťových kartách.
HDD (hard disk drive) slouží jako dlouhodobá paměť v počítači, často se nazývá také pevný disk. Data se ukládají na magnetický otočný disk. Oproti SSD, jeho současné konkurenci mezi dlouhodobými úložišti, je levnější a mívá větší kapacitu.
SSD (solid state drive) je další typ dlouhodobého úložiště. Na rozdíl od HDD je tvořený flash pamětí. Díky tomu je odolnější, protože nemá žádné pohyblivé části, a také rychlejší. Přestože jeho poměr ceny a kapacity je horší než u HDD, v současnosti pevný disk díky výše zmíněným výhodám pomalu nahrazuje.
CD a DVD jsou přenosná dlouhodobá úložiště ve tvaru disku. Data se u nich zaznamenávají a čtou opticky, pomocí laseru.
Paměťová karta je malé přenosné dlouhodobé úložiště tvořené flash pamětí. Má několik různých typů, používá se například ve fotoaparátech nebo mobilních telefonech.
Velikost paměti se udává v bajtech (B).
Paměť může být volatilní nebo nevolatilní. Z volatilní paměti všechna data zmizí, když se odpojí od elektrického proudu. Volatilní je cache, RAM a operační paměť (ta se totiž realizuje jako RAM). V nevolatilní paměti všechna data zůstávají nezávisle na připojení k elektrickému zdroji, ale většinou bývá pomalejší než volatilní. Používá se většinou jako dlouhodobé úložiště, její zástupci jsou tedy ROM, flash paměť, HDD a SSD.
NahoruSoftware označuje programy, které počítač vykonává – od jednoduchých aplikací až po složité systémy. Pomocí softwaru můžeme psát texty, upravovat fotografie, hrát hry, ale třeba i řídit provoz jaderné elektrárny. Pro porozumění tomu, jak software funguje a jak jej správně používat, je užitečné znát jeho základní druhy a vlastnosti.
- Software: typy aplikací, příklady – kancelářské aplikace, webové prohlížeče, grafické nástroje, hry, výukové programy
- Vlastnosti softwaru – desktopový či mobilní, otevřený nebo proprietární, licenční podmínky, verze, aktualizace
- Typy
souborů – textové, obrazové, zvukové, video, komprimované,
spustitelné formáty, typické přípony názvů (např.
txt, pdf, jpg, mp3, html) - Operační systémy – základní software počítače, správa souborů a zařízení, spouštění dalších programů
Software: typy aplikací, příklady
Existuje řada různých typů softwaru, pro každý typ pak máme k dispozici na výběr z více konkurenčních produktů. Mezi výrazné typy softwaru patří následující.
Prohlížeče webových stránek, které umožňují uživatelům prohlížet a interagovat s webovými stránkami. Příklady zahrnují Google Chrome, Mozilla Firefox, Microsoft Edge.
Textové procesory umožňují uživatelům psát a editovat textové soubory. Příklady zahrnují Microsoft Word, LibreOffice Writer, Dokumenty Google.
Tabulkové editory umožňují uživatelům vytvářet, editovat a analyzovat tabulky a data v nich uložená. Příklady zahrnují Microsoft Excel, LibreOffice Calc, Tabulky Google.
Grafické editory umožňují uživatelům vytvářet a editovat grafiku a obrázky. Příklady zahrnují Adobe Photoshop, GIMP, Inkscape.
Programovací jazyky umožňují vývojářům vytvářet softwarové aplikace. Příklady zahrnují Python, Java, C++. Pro přípravu programů používají programátoři vývojová prostředí, např. Visual Studio Code, PyCharm, Eclipse. Pro vývoj počítačových her se používají specializované herní enginy, např. Unity, Unreal Engine.
Systémový software umožňuje počítači fungovat správně. Příklady zahrnují operační systémy jako Windows, macOS, Linux. Dále do této kategorie také můžeme zařadit například antivirové programy.
NahoruVlastnosti softwaru
Programy provádějící určitou užitečnou činnost se označují jako aplikace. Desktopové aplikace jsou určené pro stolní počítače či notebooky. Mobilní aplikace jsou vyvíjené pro smartphony, jsou uzpůsobené např. dotykovému ovládání. Desktopové i mobilní aplikace je za účelem použití zpravidla nutné instalovat na úložiště zařízení. Naopak webové (či cloudové) aplikace zpravidla běží v internetovém prohlížeči.
Otevřený software je k dispozici i v podobě zdrojových kódů. Svobodný software mohou uživatelé používat k libovolnému účelu. Otevřený software mnohdy bývá zároveň svobodný, často bývá vyvíjený komunitou dobrovolníků. Příkladem takového softwaru je např. Linux, Gimp či LibreOffice. Podstatná část infrastruktury internetu je závislá na otevřeném/svobodném softwaru.
Proprietární software zdrojové kódy nemá k dispozici a jeho použití bývá omezeno licencí (tzv. End User License Agreement = EULA). Proprietární software obvykle zároveň bývá komerční, autor/vydavatel jej prodává za účelem zisku (nyní často formou předplatného). Příkladem komerčního proprietárního softwaru jsou Windows, Microsoft Office či aplikace v rámci Adobe Creative Cloud.
Používání komerčního softwaru bez zakoupení licence je nelegální. Trial verze softwaru lze používat zdarma po určitou dobu, obvykle za účelem vyzkoušení. Freeware je většinou proprietární software, který je možné používat zdarma.
Aplikace bývají dostupné v různých verzích. Novější verze má zpravidla vyšší číselné označení (např. aplikace verze 1.1 bude novější než verze 0.8). Povýšení na novou verzi je aktualizace či upgrade. V softwaru se mohou objevit nezamýšlené chyby, tzv. bugy. Testovací verze softwaru, která se blíží dokončení, se označuje jako betaverze. Software se v současnosti distribuuje zejména přes internet.
NahoruTypy souborů
Soubory mohou obsahovat různé typy dat. Pro uložení určitých dat se hodí konkrétní formát souboru. Ten často bývá popisován příponou názvu souboru. Jako příklad mějme soubor poznamky.txt: poznamky je samotný název souboru, přípona txt vyjadřuje, že jde o soubor s prostým textem.
Dále uvádíme příklady různých formátů:
| Zkratka | Popis |
|---|---|
| jpg | bitmapový obrázek se ztrátovou kompresí |
| bmp | bitmapový obrázek bez komprese |
| png | bitmapový obrázek s bezztrátovou kompresí |
| svg | vektorový obrázek |
| docx, doc, odt | textový dokument |
| xlsx, xls, ods | dokument tabulkového procesoru |
| pptx, ppt, odp | prezentace |
| txt | prostý text (bez formátování) |
| dokument, na různých zařízeních se zobrazuje jednotně | |
| xml | dokument se strukturovanými informacemi opatřenými značkami (tagy) |
| wav | zvuk bez komprese |
| mp3, ogg, flac, aac | zvuk s kompresí |
| zip, rar, 7z | archiv (obsahuje komprimované soubory) |
| csv | obsahuje jednoduchá tabulková data |
| exe | spustitelný program pro Windows |
| html | soubor se zdrojovým kódem webové stránky |
Organizace souborů
Soubor je sada dat, s níž jde pracovat jako s celkem. Soubory mohou být různých typů. Soubory lze umisťovat do složek neboli adresářů. Složky mohou tedy obsahovat soubory, ale i další složky (podsložky, podadresáře). Nejvyšší adresář (obsahující „vše ostatní“) se označuje jako kořenový.
Pojmenovávání souborů a složek, organizace souborů
Soubory i složky pojmenováváme tak, aby název odpovídal jejich obsahu. Pro lepší přehled v nich je také adekvátně umisťujeme do podsložek.
Příklady pojmenování a organizace
Např. ve složce spojené se školou vytvoříme podsložky týkající se předmětů, prezentaci s referátem týkajícím se historického období pojmenujeme třeba baroko.pptx. Tak snadno rozlišíme předmět i rychle najdeme konkrétní soubor.
Obsah souboru „bez názvu“ jen těžko odhadneme, aniž bychom ho otevřeli.
Snadněji se vyznáme ve složce, která obsahuje menší množství souborů, např. fotky z výletů umístíme do podsložek podle data a/nebo navštíveného místa.
V rámci běžné uživatelské práce lze soubory a složky pojmenovávat libovolně. Pokud se soubory pracujeme v rámci skriptů či příkazového řádku, je výhodné vynechat diakritiku a mezery (např. tabulka_jmena.csv).
Operace se soubory
Soubory je možné např. přejmenovávat, kopírovat či přesouvat do jiných složek. Pokud souboru upravíme příponu (např. txt na png), jeho obsah se nezmění (tedy text se nepromění v obrázek), ale mohou nastat problémy s jeho otevřením.
Při mazání souborů se tyto soubory často přesouvají do koše (v operačním systému Windows, na cloudových úložištích), odkud je lze v případě potřeby obnovit.
Úložiště
Soubory mohou být uloženy jak na našem vlastním zařízení (např. počítači, telefonu, externím pevném disku), tak na cloudu (na vzdáleném serveru). Uložení na cloud obvykle usnadňuje sdílení souborů dalším uživatelům a spolupráci na jejich úpravách. K souborům na vlastním zařízení lze zase přistupovat rychleji, i bez připojení k internetu.
U souborů/složek (na místním i cloudovém úložišti) lze obvykle nastavit, kteří uživatelé k nim budou mít přístup a jaká budou mít práva (např. čtení, úpravy).
NahoruOperační systémy
Operační systém je program, který se obvykle spouští krátkou dobu po zapnutí počítače. Zprostředkovává spouštění dalších programů/aplikací (ty mohou být určené pro konkrétní operační systém). Programy v rámci operačního systému běží jako jednotlivé procesy, soudobé operační systémy obvykle podporují běh více procesů zároveň (multitasking).
Prostřednictvím operačního systému mohou aplikace komunikovat s hardwarem (vizte schéma níže). Operační systém dále zajišťuje organizaci dat na úložišti a přístup k nim, obvykle umožňuje pracovat s uživatelskými účty či právy uživatelů. To, že mnoho činností zajišťuje operační systém, zjednodušuje do určité míry vývoj programů (aplikací).
Operační systémy se původně ovládaly zadáváním příkazů do příkazového řádku. V současnosti obvykle mají grafické uživatelské rozhraní (GUI), které umožňuje např. ovládání klávesnicí a myší či dotykem.
Některé aplikace bývají zahrnuty v samotné instalaci operačního systému, např. internetový prohlížeč, prohlížeč souborů či základní ovladače hardwaru.
Příklady operačních systémů
Mezi běžné desktopové operační systémy (určené zejména pro stolní počítače, notebooky) patří:
| Název operačního systému | Vyvíjí jej | Další informace |
|---|---|---|
| Windows | Microsoft | Nejrozšířenější systém na osobních počítačích. Je proprietární. |
| Linux | komunita vývojářů + různé společnosti | Jedná se o svobodný a otevřený software. |
| macOS | Apple | Oficiálně lze spustit pouze na počítačích Mac. |
Mezi běžné mobilní operační systémy náleží:
| Název operačního systému | Vyvíjí jej | Další informace |
|---|---|---|
| Android | V současnosti nejrozšířenější, výrobci jej uzpůsobují svým zařízením. | |
| iOS | Apple | Pouze pro zařízení značky Apple. |
Aktualizace
Operační systém jako každý další software může obsahovat bezpečnostní chyby. Ty jsou zpravidla průběžně opravovány. Bezpečnostní záplaty (a případně různá vylepšení či změny) se dostávají na zařízení uživatele jako v rámci aktualizací (též update/upgrade).
NahoruPočítačové sítě
Počítačové sítě jsou skupiny počítačů a dalších zařízení, které jsou vzájemně propojené, aby si mohly vzájemně posílat informace a sdílet zdroje (například tiskárny). Tyto sítě mohou být propojeny různými způsoby, například kabely, Wi-Fi nebo satelitním připojením. Počítačové sítě umožňují rychlé sdílení informací i na velké vzdálenosti.
Největší počítačovou sítí je internet – tím se zabýváme v prvním podtématu (např. jaký je rozdíl mezi internetem a webem). Internet však není jediná počítačová síť na světě. V dalších podtématech zkoumáme počítačové sítě obecně:
- Obecné principy – jak probíhá komunikace po síti, jaké různé typy počítačových sítí existují (síťové architektury, topologie, rozdělení sítí podle velikosti)
- Protokoly – pravidla, která určují provoz na sítích (např. TCP, UDP, IP, Wi-Fi, Bluetooth a další)
- Hardware – síťová zařízení a přenosová média, která provoz na sítích fyzicky zajišťují
Internet a web
Internet je celosvětová počítačová síť – to znamená, že propojuje počítače. Internet vznikl propojením menších počítačových sítí, které často patří soukromým vlastníkům (inter = mezi, network = síť). Internet jako celek je veřejný, nemá jednoho vlastníka ani centrální správu.
Připojení k internetu
K internetu se lze připojit drátově i bezdrátově. Při drátovém připojení se využívá infrastruktura telefonních linek (DSL) nebo kabelových televizí (v obou případech putuje po drátech elektrický signál), případně novějších optických kabelů (v nichž putuje světelný signál, který je rychlejší). Bezdrátové připojení využívá rádiové vlny vysílané buď z blízkých stanic (vysílačů) nebo satelitů na oběžné dráze Země (k připojení je potřeba mít anténu). Bezdrátové připojení k internetu umožňují skrze své vysílače také mobilní operátoři, kteří využívají technologii LTE nebo novější 5G.
K převodu analogového signálu (který putuje např. kabelem) na digitální (kterému rozumí počítače) je potřeba modem. Abychom mohli k síti připojit více zařízení, je potřeba za modem (nebo přímo do něj) přidat router (směrovač), který určuje, komu poslat která data. K routeru lze zařízení připojit pomocí síťového kabelu, ale často také bezdrátově pomocí technologie Wi-Fi (pak mluvíme o Wi-Fi routeru). Mobilní zařízení umožňují sdílet datové připojení k internetu s jinými zařízeními, tato funkce se označuje jako hotspot.
World Wide Web
World Wide Web (často zkráceně jen web) je síť propojených webových stránek. Webové stránky jsou „hypertextové dokumenty“, což znamená, že na sebe vzájemně odkazují pomocí tzv. hypertextových odkazů. Odkazy mají formu URL (Uniform Resource Locator), které zahrnuje komunikační protokol, doménové jméno a cestu k danému zdroji (např. https://fi.muni.cz/contacts). Webové stránky se píší ve značkovacím jazyce HTML, který umožňuje určit strukturu stránky, formátování textu i hypertextové odkazy.
Struktura URL
Příkladem URL je https://cs.wikipedia.org/wiki/Wi-Fi. URL začíná zkratkou protokolu, který se má použít pro komunikaci s webovým serverem (http). Za dvojtečkou a dvěma lomítky následuje doménové jméno (cs.wikipedia.org), ze kterého lze zjistit přesnou adresu webového serveru v rámci internetu. Doménové jméno má několik částí oddělených tečkou, nejvíce vpravo je tzv. doména nejvyššího řádu (org). Za lomítkem je cesta ke zdroji v rámci daného serveru (/wiki/Wi-Fi). Za otazníkem pak mohou volitelně následovat ještě parametry požadavku na server (https://www.google.cz/search?q=wifi).
K prohlížení webových stránek slouží programy označované jako webové prohlížeče neboli browsery (např. Chrome, Firefox, Edge, Safari, Opera). Prohlížeče komunikují s webovými servery podle pravidel protokolu HTTP (Hypertext Transfer Protocol), nebo jeho zabezpečného rozšíření HTTPS (S = Secure). Vyhledávání na internetu pomocí klíčových slov umožňují internetové vyhledávače (např. Google, Bing, Seznam.cz).
Další internetové služby
Internet není jen World Wide Web. Internet umožňuje i další služby, například posílání e-mailů, instant messaging (okamžité zasílání zpráv), videokonference (např. Zoom, Google Meet), streamování videa a hudby nebo přenos souborů. Infrastrukturu internetu využívají také tzv. cloudy. Cloudová úložiště (např. Google Drive, Dropbox) umožňují ukládání souborů a online přístup k nim – data jsou totiž fyzicky uložena v počítači poskytovatele cloudu, nikoliv v našem počítači. Cloudy umožňují na vzdáleném serveru nejen ukládat data, ale také provádět výpočty (tzv. cloud computing).
Bezpečnost
Z pohledu bezpečnosti je vhodné s webovými servery komunikovat prostřednictvím protokolu HTTPS, který veškerou komunikaci šifruje, což je zásadní zejména při posílání osobních údajů. Bezpečnější komunikaci mezi sítěmi zajišťuje firewall, který je jednak součástí routerů, jednak jako samostatná aplikace na počítači. Firewall kontroluje příchozí i odchozí data a pokud mají podezřelý obsah, nepustí je dál.
VPN (Virtual Private Network) je virtuální soukromá síť, tedy soukromé propojení několika počítačů v rámci internetu (který sám o sobě zabezpečený není). Propojené počítače tak mohou být kdekoliv na světě, komunikace mezi nimi je přitom zabezpečená, jako by byly součástí soukromé sítě.
NahoruPočítačové sítě: obecné principy
Počítačové sítě propojují dohromady počítače a umožňují jim vyměňovat si mezi sebou informace. Největší světovou sítí je internet, nejde však o jedinou počítačovou síť. Internet je tvořený propojením mnoha menších sítí a existují i počítačové sítě, které k internetu připojené nejsou (např. interní firemní sítě).
Komunikace po síti
Průběh komunikace po síti určují síťové protokoly. Například protokol HTTP určuje průběh komunikace s webovými servery a protokol IP slouží k nalezení cesty, kudy data po síti posílat. Data se po síti nejčastěji posílají v oddělených balíčcích, nazývaných pakety. Pakety se skládají z hlavičky, která obsahuje řídicí informace, a z vlastních dat.
Síťové architektury
Síťová architektura je návrh sítě, který určuje, jak probíhá komunikace mezi prvky sítě. Nejčastější jsou dvě architektury:
V klient-server síti mohou zařízení mít dvě různé úlohy. Server poskytuje služby, veškerá komunikace v síti jde přes něj. Typicky jde o velký počítač, který například patří nějaké firmě. Klienti jsou běžné uživatelské počítače, které si žádají služby od serveru. Když si například chceme zobrazit webovou stránku, náš počítač (klient) pošle serveru, který danou stránku provozuje, žádost o zaslání obsahu stránky.
V peer-to-peer síti jsou si všechny prvky rovny. Každý uživatel (peer) si může vyžádat služby od ostatních a na oplátku některé služby poskytuje.
Topologie
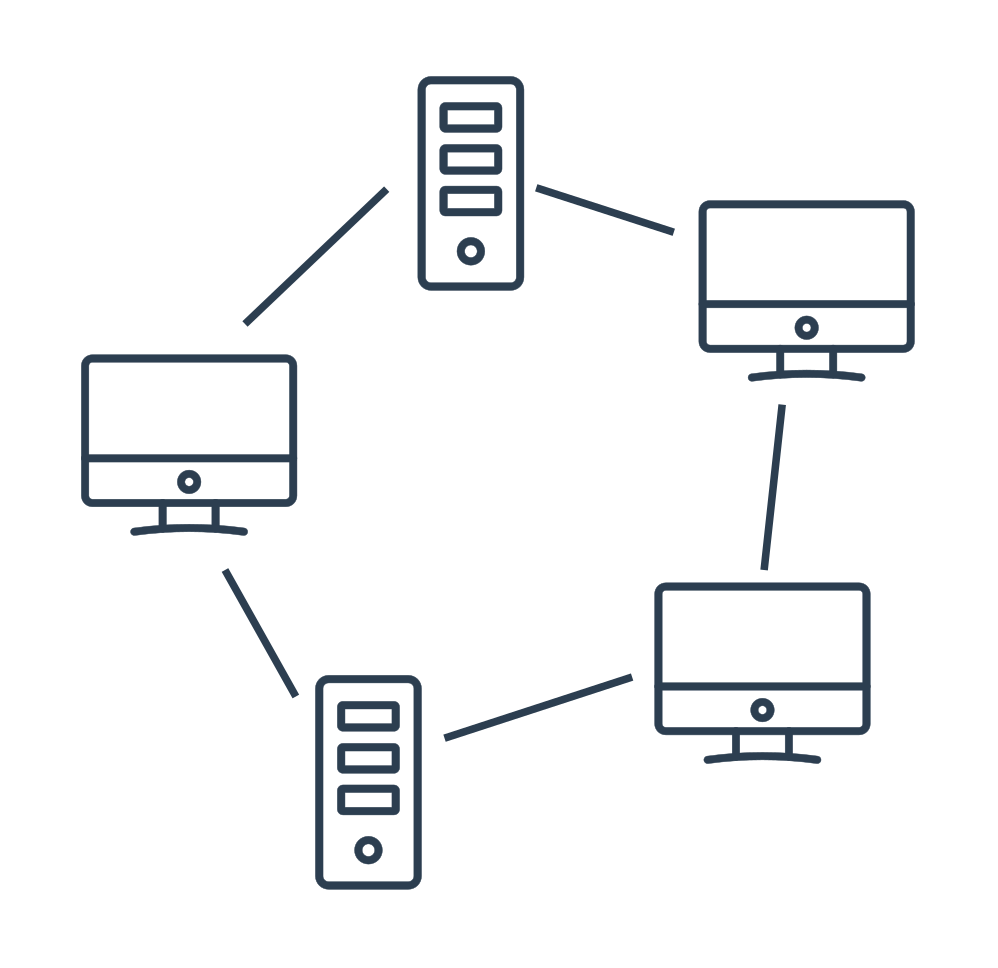
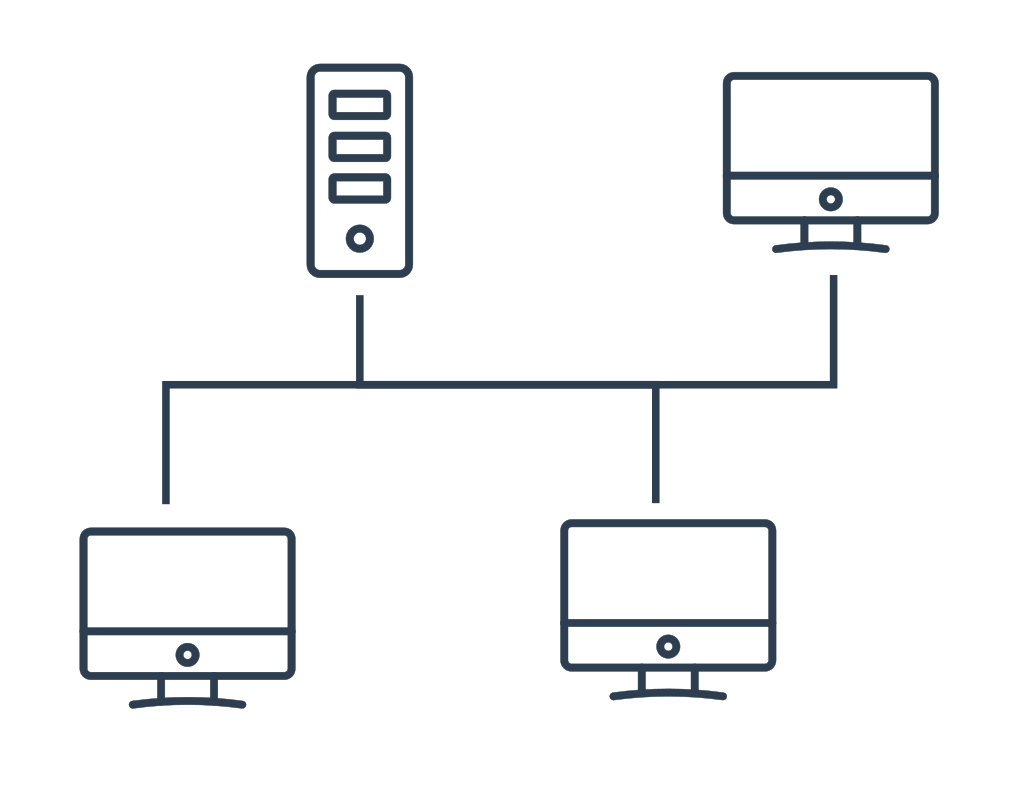
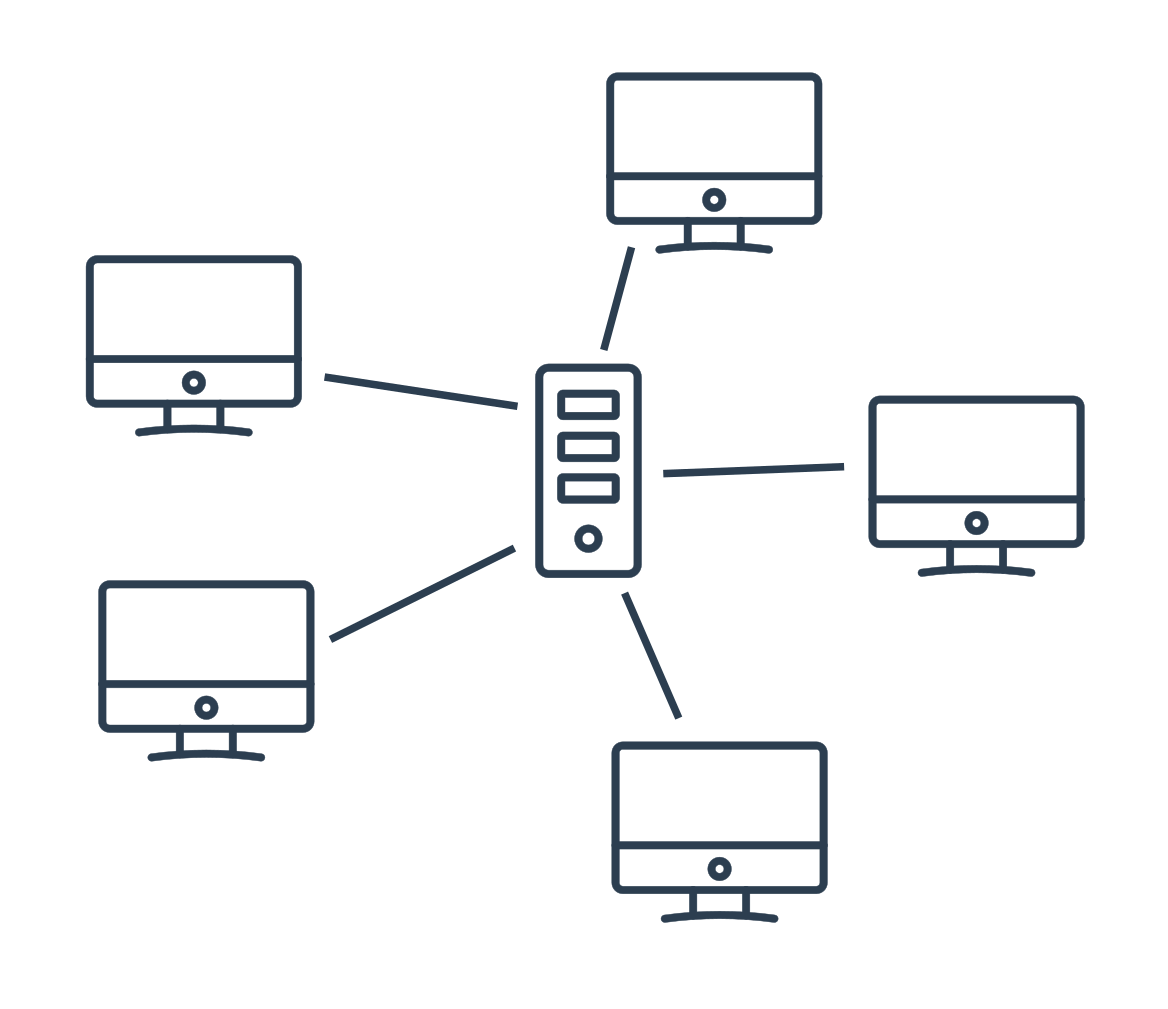
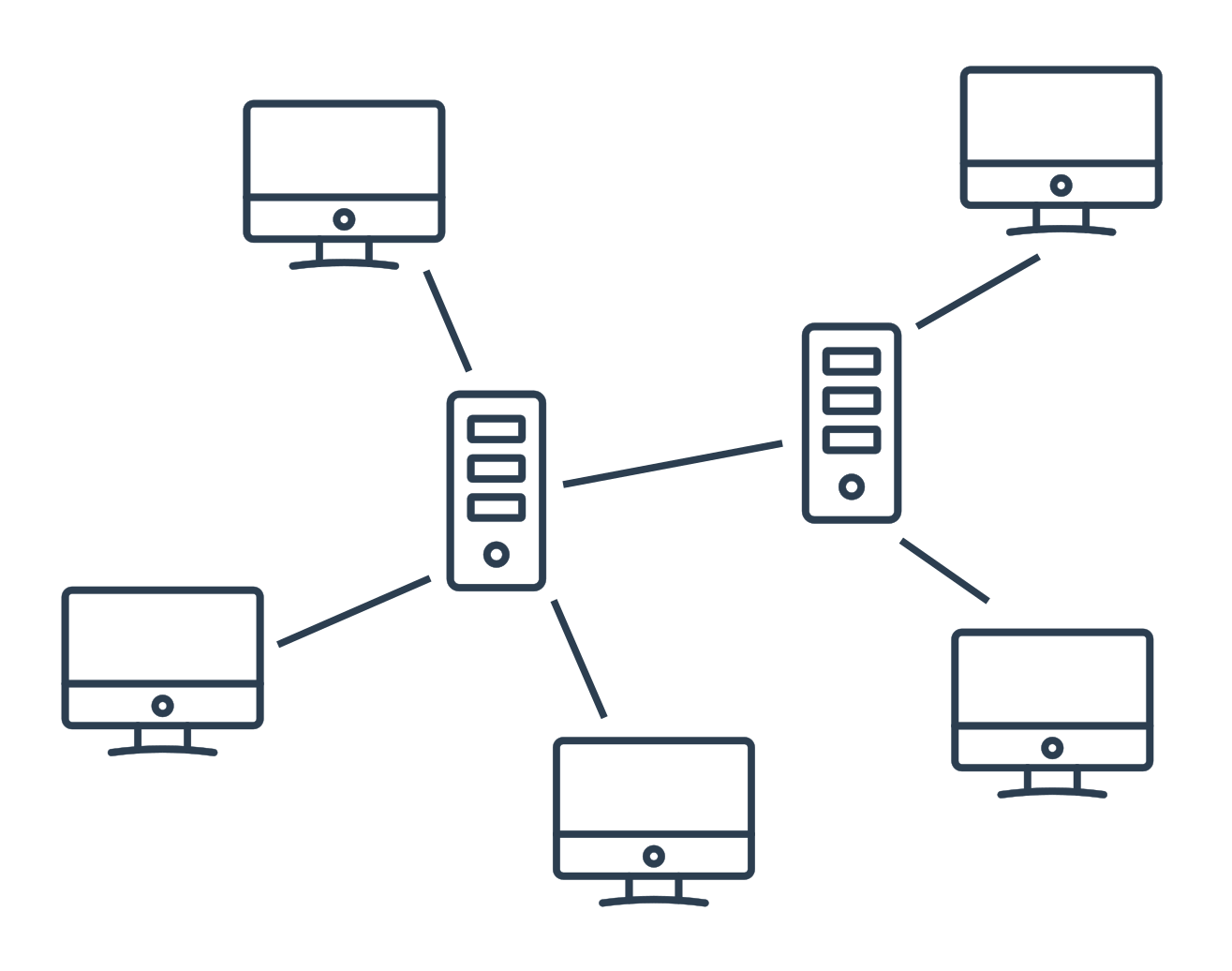
Skutečná fyzická podoba zapojení prvků do sítě se nazývá topologie. Základní typy topologií jsou kruhová, sběrnicová, hvězdicová a stromová. Každá z nich má různé výhody a nevýhody. (Např. ve sběrnicové topologii je snadné zapojení dalšího počítače do sítě, ale přenášení dat po jednom společném kabelu vede k vysoké kolizi dat.) Proto se ve skutečných sítích kombinují různé topologie dohromady.
Rozdělení sítí podle velikosti
Sítě lze také rozlišovat podle velikosti a rozsahu. Zde jsou některé vybrané typy:
- LAN (Local Area Network) – síť pokrývající malé území, například jednu budovu
- WLAN (Wireless Local Area Network) – LAN s bezdrátovým přenosem dat
- WAN (Wide Area Network) – síť, která obsluhuje velké území (Např. internet je sítí typu WAN.)
Počítačové sítě: protokoly
Provoz v počítačových sítích probíhá podle pravidel protokolů. Protokolů existuje mnoho, každý má určitou vlastní funkci.
TCP a UDP řídí přenos dat od uživatele k příjemci. UDP posílá data bez zajištění spolehlivosti, ale zato velmi rychle. Hodí se například pro přenos videohovorů, kde potřebujeme okamžitě reagovat. Kvůli nespolehlivosti UDP se však musíme smířit s občasnou horší kvalitou dat. TCP umí zajistit, že data dorazí všechna a bez chyb, avšak za cenu menší rychlosti. V současnosti přenáší většinu dat na internetu – například se využívá pro načítání webových stránek, posílání e-mailů nebo stahování souborů.
IP zajišťuje směrování, tedy hledá cestu, kudy data skrz síť půjdou. Kam doručit data zjišťuje podle IP adresy, která jednoznačně určuje každý počítač v síti. V současnosti existují dvě funkční verze protokolu: IPv4 a IPv6.
Protože IP adresy se lidem těžko pamatují, nahrazují se doménovými jmény, která bývají například součástí URL. Doménová jména jsou organizována do hierarchicky rozloženého systému, ve kterém je lze snadněji najít. Protokol DNS dokáže na dotaz z doménového jména zjistit IP adresu.
WiFi a Bluetooth jsou síťové protokoly, které přenáší data vzduchem. WiFi často slouží k vybudování malých sítí a připojování přenosných zařízení k internetu. Bluetooth se obvykle používá k propojení zařízení a přenosu dat mezi nimi na krátkou vzdálenost.
Některé další protokoly, se kterými se můžeme setkat:
- DHCP umožňuje automatickou konfiguraci počítače do sítě, mimo jiné umí přidělit IP adresu.
- HTTP komunikuje s WWW servery a umožňuje tak zobrazení WWW stránek.
- FTP dokáže přenášet soubory mezi počítači.
- SMTP posílá e-mailové zprávy.
- IMAP a POP3 umí zprostředkovat přístup k e-mailové schránce.
- IRC umožňuje posílání krátkých zpráv (chatování).
- SSH zajišťuje soukromé spojení mezi dvěma počítači.
Počítačové sítě: hardware
Hardwarová část počítačových sítí je tvořena síťovými zařízeními, která jsou propojena přenosovými médii.
Síťová karta je součást hardwaru počítače a zajišťuje komunikaci s počítačovou sítí. Od počítače si bere data pro poslání do sítě, balí je do paketů a odesílá. Také přijímá ze sítě pakety a rozbalená data předává počítači. Síťová karta je v síti jednoznačně identifikovaná MAC adresou.
Síťová zařízení
Protože signál se může při cestě přenosovým médiem zeslabit nebo poškodit, používá se opakovač. Ten opraví a zesílí přijímaný signál a následně ho pošle dál.
Hub umožňuje spojení více kabelů a dokáže tak rozvětvovat síť do více směrů. Data, která přes něj procházejí, nijak nefiltruje, pouze je rozesílá dál.
Switch a bridge spojují menší segmenty sítě. Udržují si tabulku MAC adres zařízení ve svém okolí a posílají přicházející data jen do směrů, kde se nachází jejich příjemci. Zatímco bridge propojuje pouze 2 části sítě, switch jich umí spojit více najednou.
Router propojuje větší části sítí (nebo celé sítě) dohromady. Může například připojovat lokální síť k internetu. Zajišťuje směrování dat - pro příchozí pakety se snaží najít co nejkratší cestu k cílové IP adrese.
Přenosová média
Přenosové médium může být například vzduch nebo kabel. V počítačových sítích se používají například tyto druhy kabelů:
Optický kabel se skládá z mnoha optických vláken. Signál se jím posílá v podobě světla. Přenos skrz optické kabely je velmi rychlý a málo ztrátový, jsou vhodné pro přenosy na velké vzdálenosti.
Kroucená dvojlinka a koaxiální kabel jsou tvořené kovovým vodičem. Často se používají k budování lokálních sítí.
Zapojení síťového kabelu umožňuje konektor RJ-45.
NahoruMobilní telefony
Mobilní telefony jsou běžně využívaná přenosná zařízení. Jde vlastně o miniaturní počítače. Mohou sloužit například ke komunikaci, vytváření či prohlížení digitálního obsahu. Široká dostupnost a rozšíření mobilních telefonů (smartphonů) dává lidem obrovské možnosti přístupu k informacím, ale nese s sebou i rizika (např. závislost, poruchy pozornosti).
K dispozici jsou tyto podkapitoly:
- Mobilní telefony: základy – Základní přehled o fungování mobilních telefonů, stručná historie.
- Mobilní telefony: software, připojení, platby – Operační systémy, mobilní aplikace, různé způsoby připojení (mobilní data, Wi-Fi, Bluetooth), bezkontaktní placení.
- Mobilní telefony: hardware – Hmatatelné součásti telefonů, jejich funkce a vlastnosti.
V kapitole o použití digitálních technologií lze též procvičit informace o řešení běžných technických problémů s mobilními zařízeními.
NahoruMobilní telefony: základy
Telefony původně sloužily pouze k hlasovým hovorům a byly pomocí kabelů zapojeny do telefonní sítě (pevná linka). Zhruba v 90. letech 20. století začaly být šířeji dostupné mobilní (tedy přenosné) telefony. Ty zahrnovaly zpravidla malý displej a ovládaly se větším množstvím fyzických tlačítek. Tlačítkové telefony se dnes využívají omezeně, existují např. typy s velkými tlačítky a jednoduchým rozhraním určené pro seniory.
Po uvedení prvního iPhone (2007) a operačního systému Android (2008) se čím dál více začaly vyvíjet a rozšiřovat chytré telefony neboli smartphony. Ty se ovládají hlavně dotykovým displejem, nabízí mnoho různých funkcí a široce využívají internet. Zejména smartphonům se věnuje tato kapitola.
Smartphone jako počítač
Smartphone je vlastně kapesní počítač, obsahuje hardwarové součásti podobně jako např. stolní počítače a notebooky (procesor, operační paměť, základní deska, úložiště aj.). Součásti smartphonů jsou ovšem menší a úspornější (co se týká využití energie). Energii k provozu hardwaru poskytuje akumulátor („baterie“), který lze opakovaně nabíjet. K nabíjení smartphonů a mobilních zařízení v současnosti slouží obvykle univerzální konektor USB-C.
Možnosti smartphonů, mobilní operátoři
K propojení zařízení s infrastrukturou mobilních operátorů slouží SIM karta či elektronická eSIM. Služby mobilních operátorů (volání, posílání SMS, mobilní data) bývají placené, a to sice pravidelnými úhradami (tarif) či dobíjením a vyčerpáváním financí podle potřeby (kredit).
K připojení mobilního telefonu k internetu mohou sloužit mobilní data (využívající např. technologie 5G, 4G/LTE). Pro přístup do místní sítě se používá Wi-Fi.
Pozitiva a negativa využívání smartphonů
Smartphony poskytují lidem široce dostupný přístup k internetu a informacím, mohou sloužit ke komunikaci, k práci/učení (např. tvorba multimediálního obsahu, interaktivní procvičování) i zábavě (např. hraní her). Mezi negativa patří např. vznik závislostí (na hrách, konzumaci obsahu na sociálních sítích), šíření dezinformací, kyberšikana, zhoršování soustředění nebo pozornosti.
NahoruMobilní telefony: software, připojení, platby
Software
Klíčovým softwarem na smartphonu je operační systém. Zajišťuje vzájemnou spolupráci hardwaru a aplikací. Nejrozšířenější je operační systém Android (v základu od firmy Google), zařízení značky Apple využívají systém iOS.
Update/upgrade operačního systému
Výrobci telefonů obvykle podporují aktualizace operačního systému určitou dobu po jeho uvedení na trh. U iOS je to v současnosti 6 let, u zařízení s OS Android se délka podpory liší (obvykle 3–5 let).
Různé (užitečné) funkce poskytují mobilní aplikace. Oproti aplikacím pro stolní počítače/notebooky jsou mobilní aplikace přizpůsobené ovládání dotykovým displejem. Jedna aplikace má obvykle zcela konkrétní, poměrně úzké zaměření.
Aplikace a operační systémy
- Jedna aplikace je obvykle nabízena ve verzi pro Android a iOS, tedy dva nejrozšířenější operační systémy.
- Některé aplikace jsou však k dispozici pouze pro jeden operační systém.
Mobilní operační systémy i mobilní aplikace jsou většinou od základů navrhované tak, aby jejich ovládání bylo pro uživatele co nejvíce snadné a intuitivní. K instalaci aplikací běžně slouží rozhraní Google Play (Android) či App Store (iOS).
Uživatel může zpravidla aplikacím udělit určitá oprávnění (např. přístup ke kontaktům, poloze zařízení, kameře, mikrofonu…). Je vhodné zvážit, zda daná aplikace příslušné oprávnění opravdu potřebuje. Pokud by se jednalo o škodlivou aplikaci, čím větší přístup bychom jí udělili, tím více škody by mohla napáchat.
Aplikace a operační systém se nacházejí na hardwarovém úložišti telefonu, i když často využívají posílání a přijímání dat přes internet. Uživatel zpravidla může procházet jen určité části úložiště smartphonu, např. k souborům operačního systému běžně nemá přímý přístup.
Připojení
K připojení mobilního telefonu k internetu mohou sloužit mobilní data. Mobilní sítě využívají technologických standardů 5G, 4G (LTE), značně pomalé připojení k internetu je možné prostřednictvím GPRS/EDGE (pouze tento signál je k dispozici na různých odlehlých místech, např. uprostřed lesa).
Je-li k dispozici místní síť, lze k ní telefon připojit přes Wi-Fi (obvykle v domácnosti, škole, na pracovišti).
Rozhraní Bluetooth slouží k připojení externích zařízení, např. sluchátek či reproduktorů.
Mobilní platby
K provádění bezkontaktních plateb je zapotřebí rozhraní NFC (near field communication). Díky tomu se může telefon (nebo jiné zařízení, např. chytré hodinky) chovat jako platební karta. Totožnost (platícího) uživatele je obvykle ověřována biometricky, pro proběhnutí platby musí být zařízení odemčené.
NahoruMobilní telefony: hardware
Mobilní telefony sestávají z fyzických součástí, tedy hardwaru. Ve srovnání se stolními počítači (i notebooky) jsou součásti telefonů menší a úspornější co se týče spotřeby elektrické energie.
Základní komponenty
Výpočty a logické operace provádí procesor. Procesory telefonů bývají vícejádrové, jejich taktovací frekvence se udává v GHz. Data, s nimiž telefon momentálně pracuje, jsou dočasně uložena na operační paměti. Její kapacita se pohybuje v řádu jednotek GB.
K dlouhodobému ukládání dat slouží flash paměť, obvykle čip eMMC. Typická kapacita dlouhodobého úložiště smartphonu v současné době činí zhruba 64–512 GB. Uživatelská data navíc mnohdy bývají uložena v cloudu.
Všechny komponenty telefonu (včetně např. fotoaparátu, reproduktoru) jsou připojeny k základní desce.
Akumulátor a nabíjení
Akumulátor poskytuje elektrickou energii pro provoz zařízení. Lze opakovaně nabíjet, jeho celková kapacita však postupně klesá. Kapacita akumulátoru se vyjadřuje v mAh (miliampérhodinách). K nabíjení zařízení v současnosti v rámci EU slouží jednotný port USB-C, pro jedno zařízení lze tedy využít různé nabíječky.
Dotykový displej
Dotykový displej telefonu je zároveň vstupní (registruje dotyky) i výstupní zařízení (zobrazuje obraz). Velikost úhlopříčky displeje se obvykle udává v palcích (″), u současných telefonů bývá kolem 6″. Obnovovací frekvence displeje má jednotku Hz (hertz), čím více Hz, tím je zobrazení plynulejší (např. u animací, pohybu ve hrách).
Další součásti smartphonů
- SIM karta – Vyměnitelná, zajišťuje přístup ke službám operátora.
- reproduktory – Výstupní zařízení.
- vibrační jednotka – Slouží k notifikacím či poskytování hmatové odezvy, např. při psaní na softwarové klávesnici.
- čtečka otisků prstů – Slouží k autentizaci uživatele a odemykání telefonu.
- fotoaparát – Obvykle větší množství jednotlivých kamer s vlastními snímači, liší se ohniskovou vzdáleností (tím, jak „přibližují“ scénu).
- NFC (near field communication) čip – Slouží k přenosu dat na krátkou vzdálenost, třeba při bezkontaktních platbách.
- GPS čip – Zajišťuje snímání polohy zařízení.
Telefony a životní prostředí
Výroba hardwaru smartphonů je poměrně náročná na surovinové zdroje a vyžaduje mnohé vzácné kovy (např. zlato, stříbro, niob, tantal). Co se týče přívětivosti k životnímu prostředí, je vhodné již zakoupený telefon používat co nejdéle. Servisy jsou mnohdy schopné vyměnit konkrétní rozbitou součást (např. prasklý displej, vyviklaný konektor). Již neopravitelné telefony je vhodné třídit společně s dalším elektroodpadem a tím umožnit jejich recyklaci.
Nahoru

