Výpis souhrnů
Logika a řešení problémů
Podtémata
- Logika a řešení problémů
- Logické výroky slovy
- Určování pravdivosti
- Implikace a ekvivalence
- Negace tvrzení
- Logické důsledky
- Logické výrazy
- Logické spojky a pravdivostní tabulky
- Vyhodnocování logických výrazů
- Úpravy logických výrazů
- Logické odvozování s výrazy
- Logické brány
- Logické obvody
- Logické úlohy
- Splňování podmínek
- Deduktivní úlohy
- Bludiště a hledání cest
- Plánování
Logika a řešení problémů
Logika se zabývá vyvozováním platných závěrů z daných předpokladů. Logika se používá v důkazech (tzv. matematická logika), ale i v běžném uvažování, kdy z dostupných informací odvozujeme další závěry (tzv. logické myšlení). V se zaměřujeme na rozvoj logického myšlení a využití logiky v informatice. Procvičování zde dělíme do tří témat:
- Logické výroky slovy – určování pravdivosti, vytváření slovně zapsaných výroků (bez formálního značení)
- Logické výrazy – zápis a vyhodnocování výrazů s logickými spojkami používanými v informatice (not, and, or, xor, ⇒, ⇔)
- Logické úlohy – využití logických úvah na řešení různorodých problémů (např. logické úlohy podobné sudoku, kde je potřeba splnit současně řadu podmínek)
Matematickou logiku si můžete procvičit v rámci předmětu Matematika. Kombinaci logického a algoritmického myšlení si můžete procvičit v rámci tématu Podmíněné příkazy. Logické úvahy v kombinaci s obecnými tabulkami můžete procvičit ve cvičení Logické úvahy o tabulkách v rámci tématu Tabulky: základní porozumění.
Využití logiky
Logika má v informatice široké uplatnění. Zde je několik příkladů:
- programování (podmíněné příkazy)
- výběr záznamů z databáze, které splňují určitou podmínku
- operace v grafických editorech (např. sjednocení a průnik dvou tvarů)
- dokazování (např. korektnost programu)
- návrh digitálních obvodů
- v umělé inteligenci jako jedna z metod pro dosažení inteligentního chování
- řešení logických úloh (např. sudoku)
- práce s informacemi (např. rozpoznání chybné argumentace)
Logické výroky slovy
Důležitou součástí logického myšlení je schopnost určit, zda určitý výrok platí, nebo neplatí. Zde procvičujeme tuto dovednost se slovně zapsanými výroky. Toto téma je rozdělené na několik podtémat:
- Určování pravdivosti – Zahrnuje výroky obsahující základní logické spojky (a, nebo, není), kvantifikátory (každý, některý) a nerovnosti (alespoň, nejvýše, stejně, různě). Např. „Mám v ruce alespoň tři esa nebo právě jednoho žolíka.“
- Implikace a ekvivalence – Výroky typu „pokud – pak“ a „právě tehdy, když“, které bývají méně intuitivní. Např. „Pokud nemám eso, pak mám žolíka.“
- Negace tvrzení – Tvorba tvrzení s opačnou pravdivostní hodnotou. Např. „Není pravda, že mám eso i žolíka.“ → „Nemám eso nebo nemám žolíka.“
- Logické důsledky – Vyvozování logického zavěru z dvou výroků. Např. „Pokud mám eso, mám i žolíka. Mám eso. → Mám žolíka.“
Určování pravdivosti výrazů s formálním značením si můžete procvičit v následujícím tématu nazvaném Logické výrazy.
NahoruUrčování pravdivosti
Výrok je věta nebo tvrzení, které je buď pravdivé, nebo nepravdivé. V této sekci se zabýváme právě výroky a jejich jednoduchými kombinacemi a určováním jejich pravdivosti. 
Příklady výroků
„Dnes jsem vstal v osm hodin ráno.“
„Mám na sobě červené tričko.“
„Můj bratr je starší než já.“
Příklady vět, které výroky nejsou
„Bude zítra pršet?“
„Běž spát!“
„Proč je tráva zelená?“
Složitější výroky a kombinace výroků
Kromě samotných výroků můžeme také výroky kombinovat. Výsledek takové kombinace je opět buďto pravdivý, nebo nepravdivý.
Základní kombinace a úpravy výroků
- První výrok a zároveň druhý výrok → platí oba výroky.
- První výrok nebo druhý výrok → platí alespoň jeden z výroků.
- Negace výroku, tedy “Neplatí výrok” → opak platnosti výroku; tedy pokud je výrok pravdivý, tak výsledek pravdivý nebude, a naopak.
Výroky se mohou týkat například porovnání množství nebo takzvané kvantifikace, tedy mluvení o všech objektech nebo o existenci objektu.
Kvantifikátory a jejich negace
- Pro všechny objekty platí výrok → existuje objekt, pro který neplatí výrok.
- Pro alespoň jeden objekt platí výrok/Existuje objekt, pro který platí výrok → pro žádný objekt neplatí výrok/ pro všechny objekty neplatí výrok.
- Pro žádný objekt neplatí/Neexistuje objekt, pro který platí → Pro alespoň jeden objekt platí.
Kvantifikátory: všechny objekty z ničeho
Tvrzení typu všechny objekty ze skupiny mají vlastnost jsou vždy pravdivé, pokud ve skupině žádné objekty nejsou.
Mějme krabici plnou modrých ponožek. Pak je tvrzení „všechny červené ponožky v krabici v sobě mají díru“ pravdivé.
Porovnání množství a jejich negace
- Já mám více hraček než Anička → Já mám nanejvýš tolik hraček co Anička/Já mám stejně nebo méně hraček než Anička.
- Zmrzlina stojí méně než auto → Zmrzlina je alespoň tak drahá jako auto/Zmrzlina stojí stejně nebo více než auto.
- Dneska je alespoň tak hezky, jako bylo včera → Dneska je méně hezky než bylo včera.
- A je nanejvýš tolik co B → A je více než B.
- Jsem stejně vysoký jako můj bratr → Jsem méně nebo více vysoký než můj bratr/Jsem vyšší nebo nižší než můj bratr.
Podrobnější rozbor negací najdete dále v sekci Negace tvrzení.
NahoruImplikace a ekvivalence
Implikace a ekvivalence jsou složitější spojky, kterými je možné spojovat výroky.
Implikace
Implikace jsou tvrzení typu pokud–pak, konkrétněji pokud platí předpoklad, pak platí závěr. Pokud předpoklad neplatí, celé tvrzení je vždy pravdivé. Pokud platí předpoklad, pak je tvrzení pravdivé právě tehdy, když je pravdivý závěr.
Příklady implikací
- „Pokud bude svítit slunce, pak půjdu ven.“
- „Pokud mi dnes zavolá babička, pak s ní půjdu do kina.“
Ekvivalence
Ekvivalence jsou tvrzení typu právě tehdy, když, konkrétněji první výrok platí právě tehdy, když platí druhý výrok. Ekvivalence je pravdivá, pokud jsou oba výroky pravdivé, nebo pokud jsou oba výroky nepravdivé. Pokud je jeden z výroků pravdivý a druhý nepravdivý, pak je celé tvrzení nepravdivé.
Příklady ekvivalencí
- „Přišel jsem do školy právě tehdy, když tam přišel pan učitel.“
- „Bábovku jsem měl ke snídani právě tehdy, když ji večer předtím mamka pekla.“
Čas, místo a příčina
Obecně platí, že pravdivost výroků závisí i na konkrétním čase a místě. Takže například pravdivost výroku „Pokud jsem přišel domů dřív než můj táta, pak jsem přišel před pátou.“ závisí na dni, kdy ho vyhodnocuji. Může se stát, že dnes je pravdivý, ale včera nebyl.
Pokud je někde použita spojka „právě tehdy, když“, je jí myšlen souběh pravdivostí daných událostí. Takže například „Přišel jsem do školy právě tehdy, když tam přišel pan učitel.“ se překládá na „Buď jsme přišli do školy oba, nebo ani jeden z nás.“. Mohli jsme klidně přijít každý v jiný čas, není nutné, abychom vešli do dveří zároveň. Stejně to je i u implikace. Vztah pokud–pak se netýká ani času, ani není část za pak nutně způsobena částí po pokud.
Úpravy na ekvivalentní tvrzení
Jednou z možností jak pracovat s implikací nebo ekvivalencí je upravit si tvrzení na jiné ekvivalentní. K tomu mohou nejvíce pomoci pravidla v sekci úpravy logických výrazů, ale některá si ukážeme i tady. Všechna vyplývají z definic.
Úpravy implikace a ekvivalence
- Implikaci můžeme přepsat pomocí nebo. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat jako „Nebude svítit slunce nebo půjdu ven.“, nebo dlouze „Nebude svítit slunce, nebo bude svítit slunce a půjdu ven.“.
- Takzvaná obměna implikace je úprava implikace na jinou ekvivalentní implikaci. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat na „Pokud nepůjdu ven, pak nebude svítit slunce.“
- Ekvivalence se dá přepsat na dvě implikace takto: „Slunce bude svítit právě tehdy, když půjdu ven.“ můžeme přepsat na „Pokud bude svítit slunce, pak půjdu ven, a zároveň pokud půjdu ven, pak bude svítit slunce.“
- Ekvivalenci můžeme přepsat i na kombinaci „a zároveň“ a „nebo“. „Slunce bude svítit právě tehdy, když půjdu ven.“ pak bude „Bude svítit slunce a půjdu ven, nebo nebude svítit slunce a nepůjdu ven.“
Negace tvrzení
Negace tvrzení je opět tvrzení, avšak s opačnou pravdivostní hodnotou. Jinak řečeno, negace pravdivého tvrzení je tvrzení nepravdivé, a negace nepravdivého tvrzení je tvrzení pravdivé. Z toho mimo jiné plyne, že ve všech situacích, které mohou nastat, je pravdivé právě jedno: buďto dané tvrzení, nebo jeho negace.
Příklady
Příklady negací tvrzení
- „Dnes jsem vstal v osm hodin ráno.“ → „Dnes jsem nevstal v osm hodin ráno.“
- „Mám na sobě červené tričko.“ → „Nemám na sobě červené tričko.“
- „Můj bratr je starší než já.“ → „Můj bratr není starší než já.“
Negace tvrzení mluví o stejných objektech a jejich vlastnostech jako původní tvrzení, jen obrací jeho pravdivost za všech situací.
Příklady tvrzení, které nejsou negací původního tvrzení
- „Dnes jsem vstal v osm hodin ráno.“ a „Dva plus tři je šest.“
- „Mám na sobě červené tričko.“ a „Nemám na sobě modré ponožky.“
- „Můj bratr je starší než já.“ a „Můj bratr nemá na sobě červené tričko.“
Negace tvrzení se spojkami
Negovat se dají i složitější tvrzení obsahující spojky.Negace tvrzení se spojkami
Jedním ze způsobů negace složitějších tvrzení je prosté přidání “není pravda, že” na začátek věty. Pokud chceme tvrzení negovat sofistikovaněji, můžeme to dělat například následujícími způsoby:
- „Platí A a zároveň platí B.“ → „Neplatí A nebo neplatí B.“
- „Platí A nebo platí B.“ → „Neplatí A a zároveň neplatí B.“
- „Pokud platí A pak platí B.“ → „Platí A a zároveň neplatí B.“
- „Platí A právě tehdy, když platí B.“ → „Platí A a zároveň neplatí B, nebo neplatí A a zároveň platí B.“
- „Neplatí A.“ → „Platí A.“
Zvláštnosti a chytáky
Zvláštností jsou negace takzvaných tvrzení s kvantifikátory. To jsou taková tvrzení, která obsahují slova typu všichni, žádný, alespoň jeden, existuje a podobné.
Všechny objekty mají vlastnost
Ke znegování tvrzení typu všechny objekty mají vlastnost stačí říct, že alespoň jeden z objektů chtěnou vlastnost nemá. Stejně tak ke znegování tvrzení typu žádný objekt nemá vlastnost stačí říct, že alespoň jeden z objektů chtěnou vlastnost nemá.
- „Všichni draci mají křídla“ → „Existuje alespoň jeden drak, který křídla nemá.“
- „Žádný pes nemá rád párky“ → „Existuje alespoň jeden pes, který má rád párky.“
Existuje objekt s vlastností
Ke znegování tvrzení typu existuje objekt s vlastností máme dvě možnosti. Buďto řekneme, že žádný objekt neexistuje, nebo že žádný objekt tu vlastnost nemá.
- „Existuje člověk s čistým svědomím.“ → „Žádný člověk nemá čisté svědomí.“
- „Existuje jednorožec bez sedla.“ → „Buďto žádný jednorožec neexistuje, nebo mají všichni jednorožci sedlo.“
- „Existuje hrnek bez ucha.“ → „Všechny hrnky mají alespoň jedno ucho.“
Dalším typem jsou negace s porovnáváním množství. To jsou taková tvrzení, která obsahují slova typu alespoň, nanejvýš, stejně, více, méně a podobné.
Porovnání množství a jejich negace
Při negování porovnávání množství musíme brát v potaz i možnost, že obou věcí je stejně. Pokud je něčeho ostře méně, negujeme na stejně nebo více a podobně.
- „A je více než B.“ → „A je nanejvýš tolik co B.“/„A je stejně nebo méně než B.“
- „A je méně než B.“ → „A je alespoň tolik co B.“/„A je stejně nebo více než B.“
- „A je alespoň jako B.“ → „A je méně než B.“
- „A je nanejvýš tolik co B.“ → „A je více než B.“
- „A je stejně jako B.“ → „A je méně nebo více než B.“
Konkrétní příklady porovnání množství a jejich negace
- „Já mám více hraček než Anička.“ → „Já mám nanejvýš tolik hraček co Anička.“/„Já mám stejně nebo méně hraček než Anička.“
- „Zmrzlina stojí méně než auto.“ → „Zmrzlina je alespoň tak drahá jako auto.“/„Zmrzlina stojí stejně nebo více než auto.“
- „Dneska je alespoň tak hezky, jako bylo včera.“ → „Dneska je méně hezky než bylo včera.“
- „V Praze je nanejvýš tolik stupňů co v Brně.“ → „V Praze je více stupňů než v Brně.“
- „Jsem stejně vysoký jako můj bratr.“ → „Jsem méně nebo více vysoký než můj bratr.“/„Jsem vyšší nebo nižší než můj bratr.“
Logické důsledky
Odvozování logických důsledků z předpokladů je velmi důležitá dovednost. Nejde jen o samotné odvozování, ale i o schopnost rozpoznat, jestli nějaké tvrzení plyne z faktů, které známe.
V této sekci si ukážeme hned několik druhů odvozování.
Řetězení implikací
Kdykoli z prvního faktu plyne druhý, a z druhého plyne třetí, pak z prvního faktu bude plynout i fakt třetí.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Pokud jdeme plavat, pak prší.“ dokážeme vyvodit, že každé úterý prší.
- Z předpokladů „Všichni čerti mají rohy.“ a „Pokud má někdo rohy, pak má i ocas.“ můžeme vyvodit, že všichni čerti mají ocas.
- Z předpokladů „Všechno ze dřeva hoří.“ a „Všechny pochodně jsou ze dřeva.“ můžeme vyvodit, že všechny pochodně hoří.
Implikace s pravdivým předpokladem
Pokud máme implikaci, která má platný předpoklad, pak nutně platí i její závěr.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Dnes je úterý.“ dokážeme vyvodit, že dnes jdeme plavat.
- Z předpokladů „Všichni čerti mají rohy.“ a „Jsem čert.“ můžeme vyvodit, že mám rohy.
Implikace s nepravdivým závěrem
Pokud máme implikaci, která má neplatný závěr, pak nutně nesmí platit její předpoklad. To je proto, že kdyby platil předpoklad, pak by musel platit i závěr, o kterém víme, že neplatí.
Příklady
- Z předpokladů „Každé úterý chodíme plavat.“ a „Dnes nejdeme plavat.“ dokážeme vyvodit, že dnes nemůže být úterý.
- Z předpokladů „Všichni čerti mají rohy.“ a „Nemám rohy.“ můžeme vyvodit, že nejsem čert.
Vyvozování z implikace a ekvivalence
Při vyvozování závěrů z implikací a ekvivalencí můžeme postupovat více způsoby. Jednou z možností je si vzít hodnoty z vyvozovaného závěru a dosadit je do původní implikace či ekvivalence.
Příklad vyvozování dosazením
Mějme zadanou ekvivalenci „Autíčko je v šuplíku právě tehdy, když je zelené.“. Pak závěry „Všechna autíčka v šuplíku jsou zelená.“ a „Žádné červené autíčko není v šuplíku.“ jsou pravdivé, ale nemůžeme vyvodit „V šuplíku je červené autíčko.“ nebo „Alespoň jedno zelené autíčko je mimo šuplík.“. Proč? Ukažme si postup na prvním závěru („Všechna autíčka v šuplíku jsou zelená.“). Dosadíme si tedy do původní ekvivalence pravdu za „autíčko je v šuplíku“ a dostaneme „Pravda právě tehdy, když je autíčko zelené.“, což je totéž jako „Autíčko je zelené.“. Předpokládali jsme libovolné autíčko v šuplíku a dostali, že je zelené. Takže musí být pravda, že „Všechna autíčka v šuplíku jsou zelená.“.
Další možností je upravit si tvrzení na jiné ekvivalentní. K tomu mohou nejvíce pomoci pravidla v sekci úpravy logických výrazů, ale některá si ukážeme i tady. Všechna vyplývají z definic.
Úpravy implikace a ekvivalence
- Implikaci můžeme přepsat pomocí nebo. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat jako „Nebude svítit slunce nebo půjdu ven.“, nebo dlouze „Nebude svítit slunce, nebo bude svítit slunce a půjdu ven.“.
- Takzvaná obměna implikace je úprava implikace na jinou ekvivalentní implikaci. „Pokud bude svítit slunce, pak půjdu ven.“ můžeme přepsat na „Pokud nepůjdu ven, pak nebude svítit slunce.“
- Ekvivalence se dá přepsat na dvě implikace takto: „Slunce bude svítit právě tehdy, když půjdu ven.“ můžeme přepsat na „Pokud bude svítit slunce, pak půjdu ven, a zároveň pokud půjdu ven, pak bude svítit slunce.“
- Ekvivalenci můžeme přepsat i na kombinaci „a zároveň“ a „nebo“. „Slunce bude svítit právě tehdy, když půjdu ven.“ pak bude „Bude svítit slunce a půjdu ven, nebo nebude svítit slunce a nepůjdu ven.“
Pokud preferujete grafické znázornění, můžete si implikace zobrazovat pomocí diagramů. Část u pokud vyznačíme jako menší kruh a část za pak jako větší okolo toho menšího.
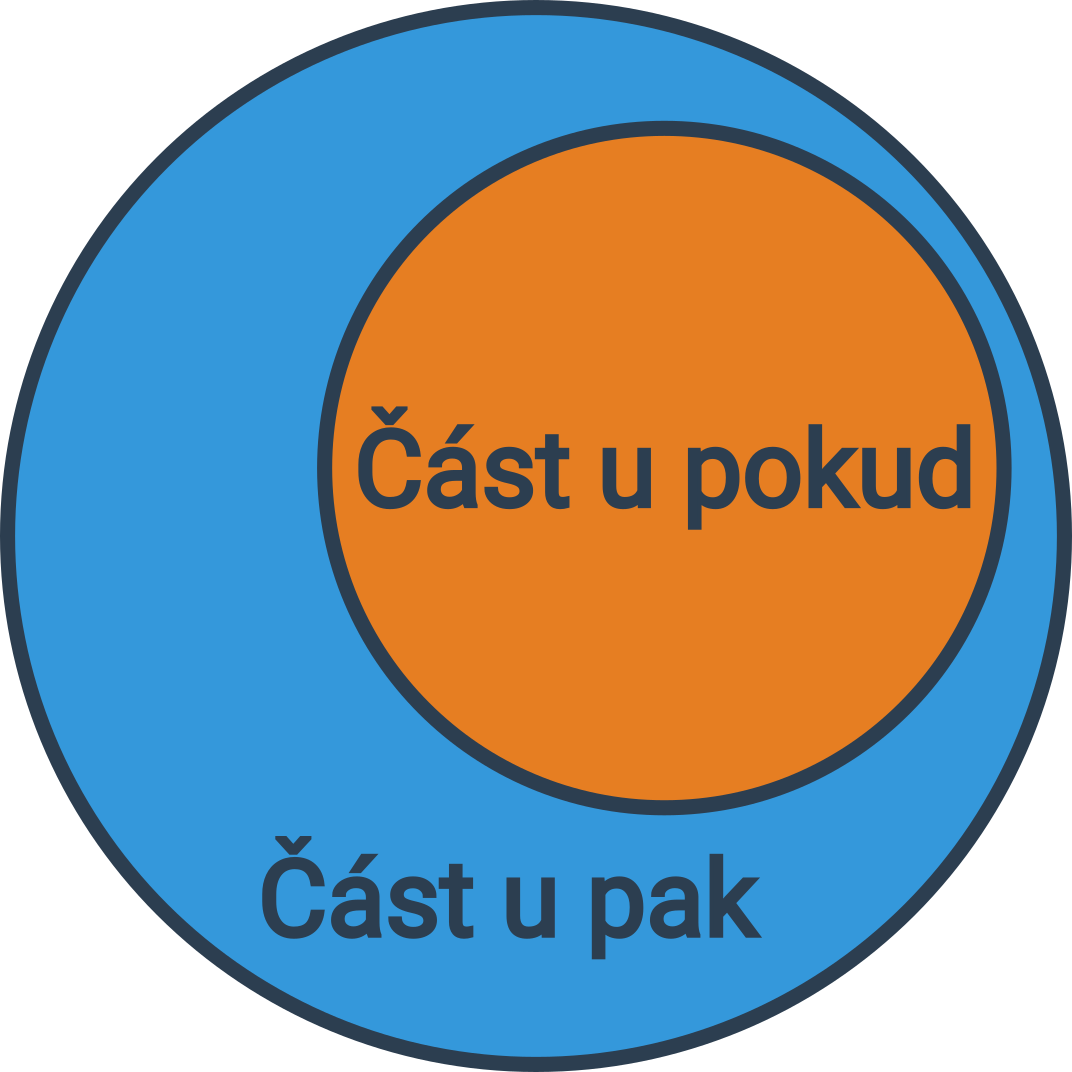
Diagramy
Mějme opět výrok „Pokud bude svítit slunce, pak půjdu ven.“ Výrok „bude svítit slunce“ vyznačíme jako menší kruh a výrok „půjdu ven“ jako větší okolo toho menšího.
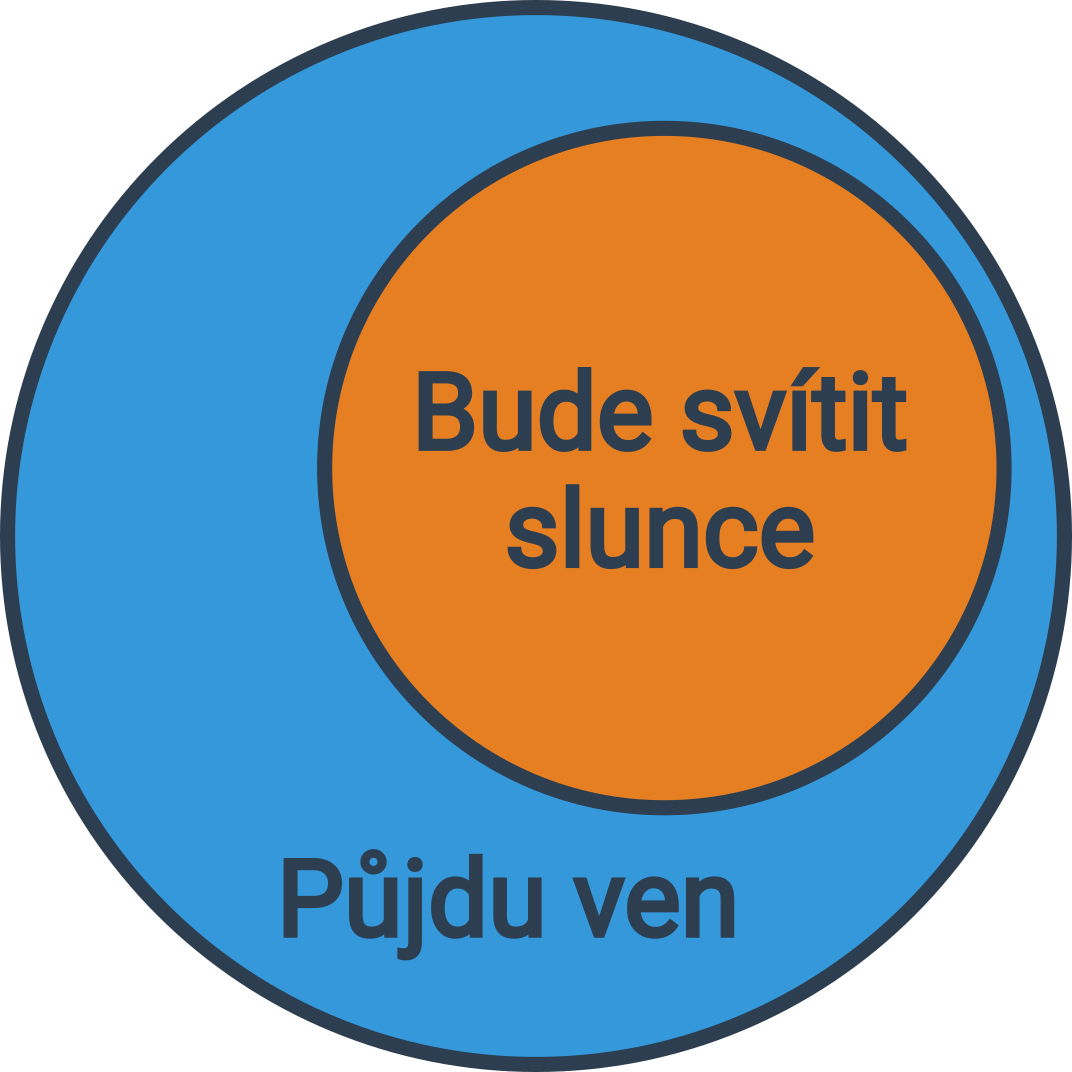
Při vyvozování závěrů se pak stačí podívat na obrázek a určit, kde se chtěná situace nachází.
Ukažme si to na příkladu. Ptáme se, jestli může nastat situace, kdy půjdu ven když nebude svítit slunce. To může nastat v místě diagramu, které je uvnitř modrého kruhu, ale je mimo oranžový kruh. Taková oblast na diagramu opravdu existuje, a proto může taková situace nastat.
Logické výrazy
V tomto tématu pracujeme s logickými výrazy s formálním značením (např. A or B), přičemž některé logické spojky značíme pomocí anglických slov (and, or, not). Toto značení je v informatice běžné, používá se například v mnohých programovacích jazycích. Téma dělíme na následující podtémata:
- Logické spojky a pravdivostní tabulky – význam jednotlivých logických spojek, přepisování z běžného jazyka do informatické notace (and, or, not, xor, ⇒, ⇔)
- Vyhodnocování logických výrazů – vyhodnocení složených výrazů kombinujících více logických spojek
- Úpravy logických výrazů – přepis na ekvivalentní výraz, který vypadá jinak, ale má vždy stejnou pravdivostní hodnotu
- Logické odvozování s výrazy – odvozování závěrů z předpokladů, kterých může být i více
Práci s logickými výroky si můžete dále procvičit i v různých jiných zápisech:
- Logické výroky slovy – výroky v běžném jazyce
- Logika v rámci předmětu matematika – práce s výroky v matematické notaci (∧,∨,¬)
- Logické výrazy v Pythonu – práce s logickými výrazy v kontextu programování
Logické spojky a pravdivostní tabulky
Pravdivostní hodnoty
V informatice používáme většinou zaměnitelně následující:
- 1 = true = pravda
- 0 = false = nepravda
Logické spojky
| Zápis | Název | Význam |
|---|---|---|
| \text{ not } X | negace | neplatí X |
| X \text{ and } Y | konjunkce, a zároveň | X a Y platí současně |
| X \text{ or } Y | disjunkce, nebo | platí alespoň jedno z X a Y |
| X \text{ xor } Y | exkluzivní nebo | platí právě jedno z X a Y |
| X \Rightarrow Y | implikace, jestliže-pak | pokud platí X, pak platí i Y |
| X \Leftrightarrow Y | ekvivalence, právě když | X platí právě tehdy, když platí Y |
Pravdivostní tabulka logických operací
| X | Y | X \text{ and } Y | X \text{ or } Y | X \text{ xor } Y | X \Rightarrow Y | X \Leftrightarrow Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
Vyhodnocování logických výrazů
Vyhodnocení logického výrazu si můžeme představit jako zjištění, jestli je pravdivý nebo nepravdivý. U jednoduchého výroku jeho vyhodnocení odpovídá jeho pravdivosti, ale u složitějších výroků s logickými spojkami jde o kombinaci pravdivostí jednotlivých podvýroků pomocí spojek.
Například spojka and se vyhodnotí na pravdu (true, 1) právě tehdy, když jsou oba výroky pravdivé.
Tedy 1 and 1 = 1, ale například 1 and 0 = 0.
Pravdivostní tabulka logických operací
| X | Y | X \text{ and } Y | X \text{ or } Y | X \text{ xor } Y | X \Rightarrow Y | X \Leftrightarrow Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
Úpravy logických výrazů
Úpravy logických výrazů je vhodné provádět například tehdy, když chceme určit pravdivost daného výroku nebo porovnat, jestli jsou dva výroky shodné. K tomu se hodí základní přepisová pravidla.
Přepis základních logických spojek
| Výrok | Ekvivalentní výrok |
|---|---|
| \text{not not } X | X |
| \text{not } (X \text{ and } Y) | (\text{not } X) \text{ or (not } Y) |
| \text{not }(X \text{ or }Y) | (\text{not } X) \text{ and (not } Y) |
Přepis implikace, ekvivalence a operace xor
| Výrok | Ekvivalentní výrok |
|---|---|
| X \Rightarrow Y | (\text{not } X) \text{ or } Y |
| X \Rightarrow Y | (\text{not } Y) \Rightarrow (\text{not } X) |
| X \Leftrightarrow Y | (X \Rightarrow Y) \text{ and } (Y \Rightarrow X) |
| X \Leftrightarrow Y | (X \text{ and } Y) \text{ or (not } X \text{ and not } Y) |
| X \text{ xor } Y | (X \text{ and not } Y) \text{ or (not } X \text{ and } Y) |
| \text{not } (X \Rightarrow Y) | X \text{ and not } Y |
| \text{not } (X \Leftrightarrow Y) | X \text{ xor } Y |
| \text{not } (X \text{ xor } Y) | X \Leftrightarrow Y |
Analogické zákony jako při počítání s čísly
Pro logické operace and a or také platí komutativní (1. a 2. řádek následující tabulky), asociativní (3. a 4. řádek) a distributivní zákony (5. a 6. řádek):
| Výrok | Ekvivalentní výrok |
|---|---|
| X \text{ and } Y | Y \text{ and } X |
| X \text{ or } Y | Y \text{ or } X |
| (X \text{ and }Y) \text{ and } Z | X \text{ and } (Y \text{ and }Z) |
| (X \text{ or } Y) \text{ or } Z | X \text{ or } (Y \text{ or } Z) |
| X \text{ and } (Y \text{ or } Z) | (X \text{ and } Y) \text{ or } (X \text{ and } Z) |
| X \text{ or } (Y \text{ and } Z) | (X \text{ or } Y) \text{ and } (X \text{ or } Z) |
Další cvičení s trochu jinou notací najdete i na umíme matiku.
NahoruLogické odvozování s výrazy
Logické odvozování s pomocí logických výrazů je formální varianta odvozování logických důsledků slovy.
Jde o proces, kdy dostaneme několik logických výrazů (faktů) a odvozujeme z nich jiný výraz (závěr). Nemusíme ale nutně jen odvozovat nové závěry, můžeme se i například pokoušet rozhodnout, jestli nějaký dodaný výrok plyne z jiných.
Říkáme, že výraz se dá odvodit (tedy vyplývá) ze zadaných výrazů právě tehdy, když platí ve všech případech, kdy platí všechny zadané výrazy.
Příklady
- Z výrazu X \text{ and } Y můžeme odvodit X, protože kdykoli platí X \text{ and } Y, musí platit X i Y, a tím spíš musí platit i samotné X.
- Z výrazů X \text{ or } Y a \text{not } X můžeme odvodit Y. Aby bylo splněno X \text{ or } Y, musí platit X nebo Y, ale X platit nemůže. Proto platí Y.
- Z výrazů X \Leftrightarrow Y a X můžeme odvodit Y. Výraz X \Leftrightarrow Y říká, že Y má vždy stejnou hodnotu jako X. Z pravdivosti X tak můžeme odvodit pravdivost Y.
Logické brány
Logické spojky jsou v počítači reprezentovány součástkami, kterým se říká logické brány. Z logických bran se pak dají skládat složitější logické obvody, které dokáží například sčítat nebo násobit čísla.
Příklady logických bran
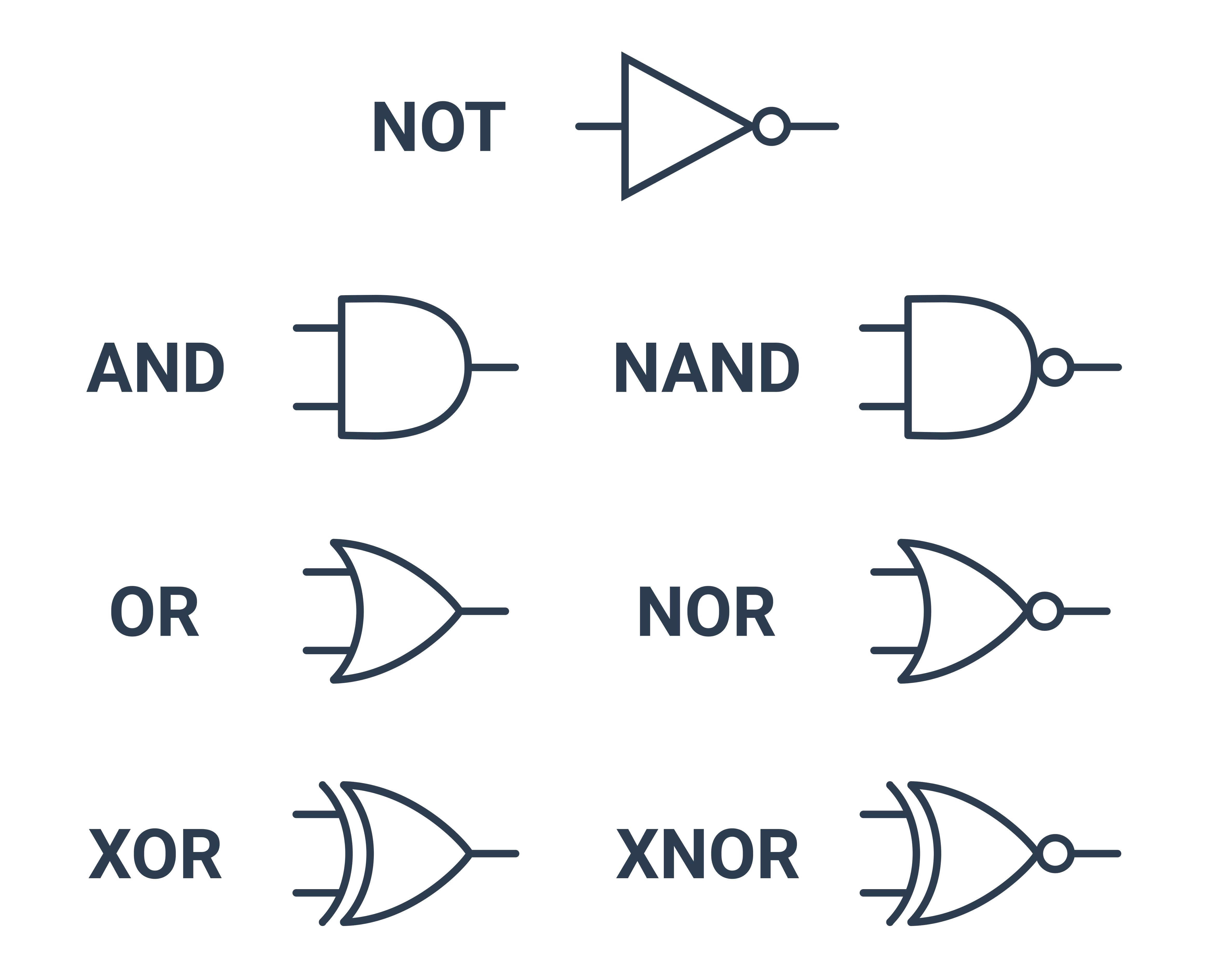
Negace
Negace se u logických bran značí kolečkem na výstupu. Samotná negace má jeden vstup a jeden výstup, a značí se trojúhelníkem s kolečkem.
Známé spojky and, or a xor mají své vlastní značky a jejich negace se tvoří přidáním kolečka na výstup. Spojka nand značí negaci od and, tedy not and, spojka nor značí negaci od or, tedy not or, a spojka xnor značí negaci od xor, tedy not xor.
NahoruLogické obvody
Logické spojky jsou v počítači reprezentovány součástkami, kterým se říká logické brány. Z logických bran se pak dají skládat složitější logické obvody, které dokáží například sčítat nebo násobit čísla. Logický obvod je složen z více bran takovým způsobem, že výstup jedné brány je použit jako vstup do jiné brány. 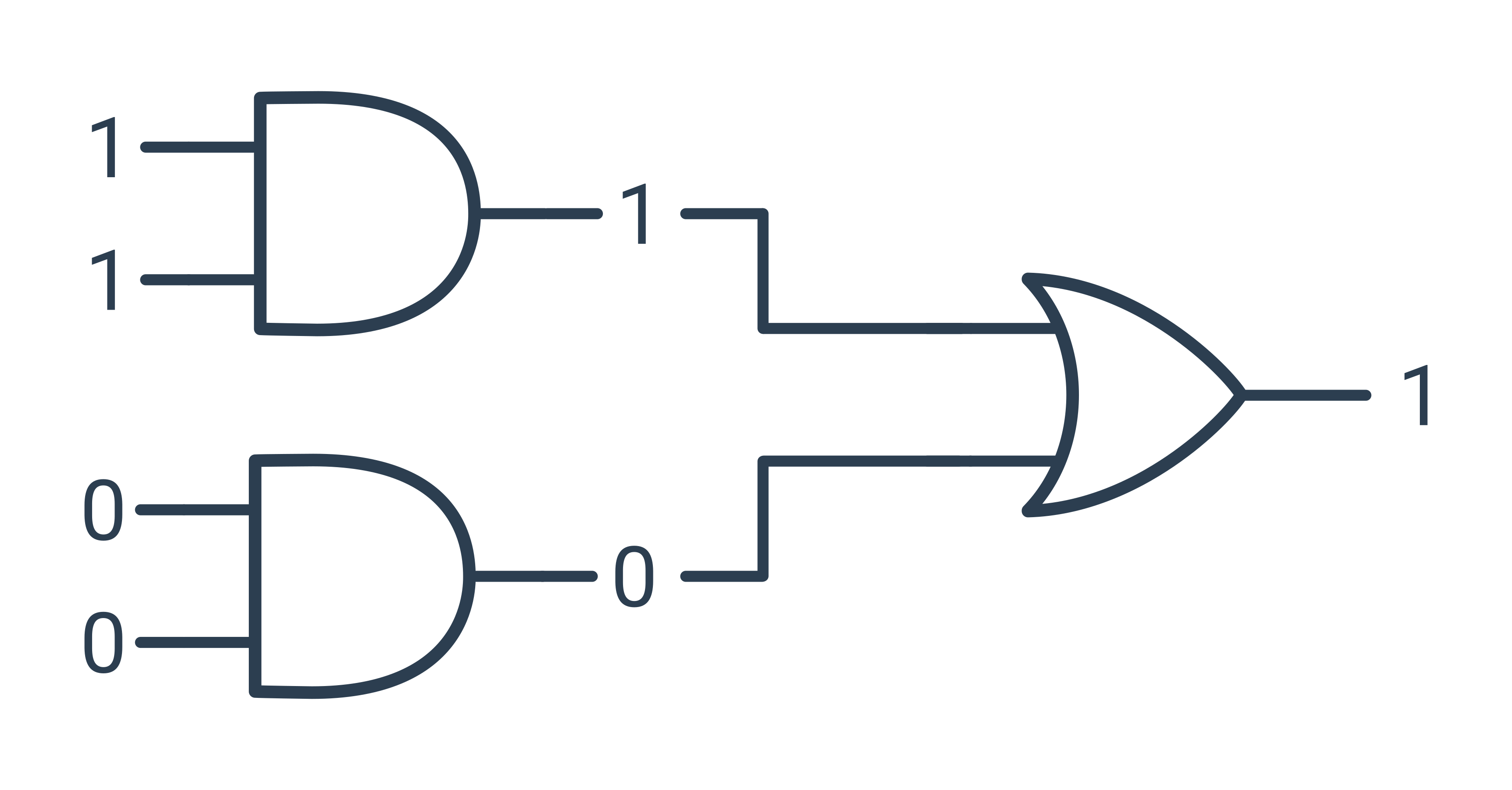
Obvody se dají i kombinovat. Spuštění dvou obvodů zároveň vedle sebe se říká paralelní zapojení obvodů. Spuštění dvou obvodů po sobě tak, že druhý obvod využívá na vstupu výstup z prvního obvodu, se říká sekvenční zapojení obvodů. 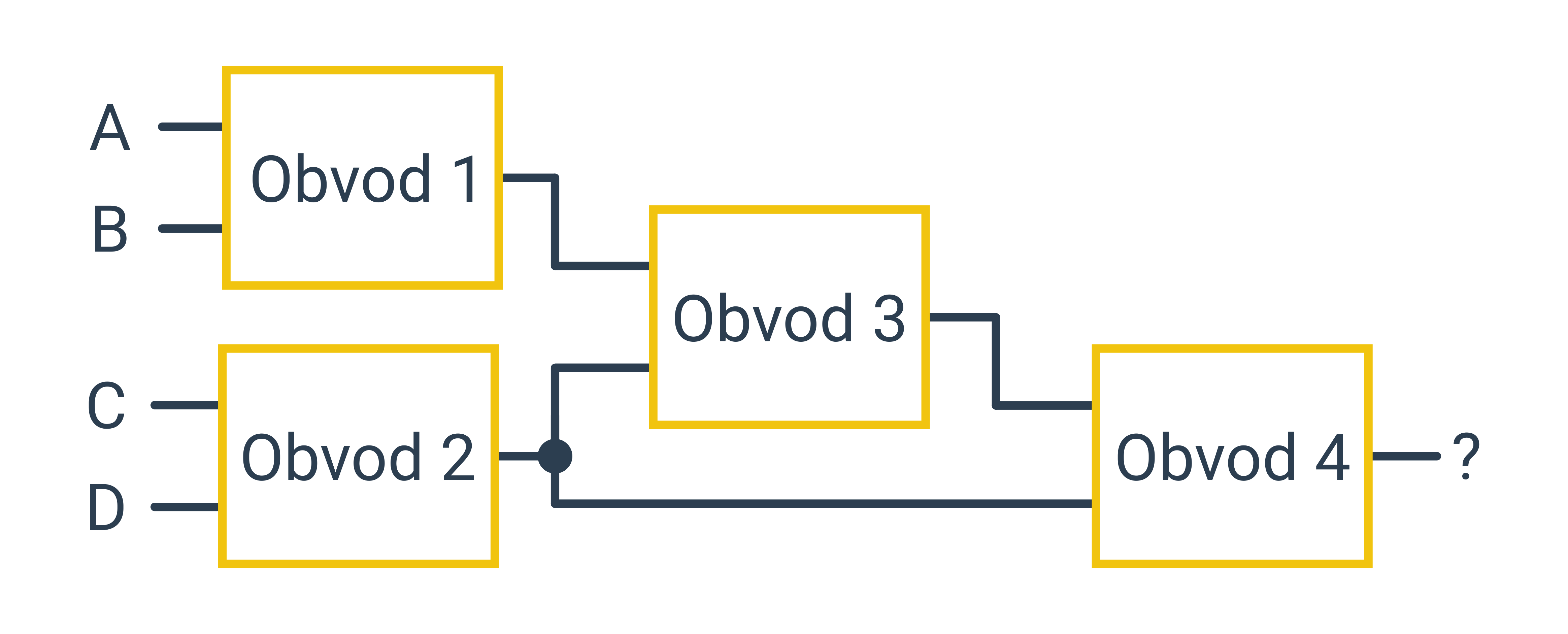
Výstup jednoho obvodu může být použit jako vstup více obvodům. Takové posílání vstupu do dvou směrů se značí plným kolečkem.
Příkladem skládání jednoduchých obvodů do většího je sčítání pomocí obvodů, kdy se například obvod pro sčítání čtyřbitového čísla dá složit jako čtyři jednobitové sčítačky v řadě. 
Logické úlohy
V tomto tématu si můžete procvičit schopnost řešit různorodé logické úlohy:
- Splňování podmínek – úlohy trénující schopnost splnit řadu zadaných omezení současně (jako např. v sudoku)
- Deduktivní úlohy – úlohy trénující schopnost zkombinovat související informace a odvodit z nich platný logický závěr
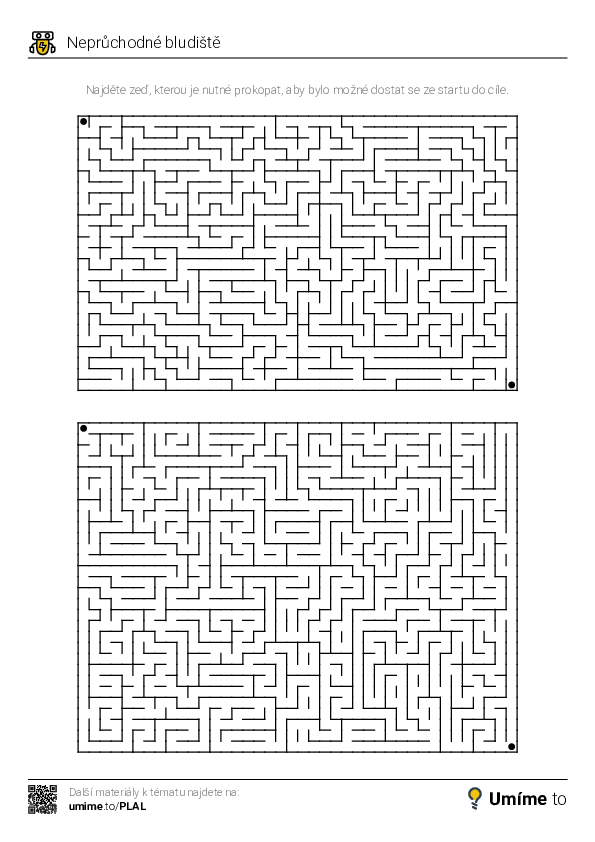
- Bludiště a hledání cest – úlohy trénující schopnost najít cestu do cíle (např. různá netradiční bludiště včetně skákání a prokopávání zdí)
- Plánování – úlohy trénující schopnost najít posloupnost kroků k dosažení požadovaného stavu
Splňování podmínek
V těchto úlohách si procvičíte schopnost splnit řadu zadaných omezení současně.
NahoruDeduktivní úlohy
Zde najdete úlohy, kde musíte ze zadaných informací vyvodit správné závěry za použití logických úvah. Takovému vyvozování závěrů z daných pravdivých předpokladů se říká právě dedukce.
Pracovní listy
Kromě interaktivních úloh jsou k dispozici i pracovní listy na vytištění (s tématem pravdomluvců a lhářů):
- Poctivci a padouši: dvojice – pracovní list + řešení
- Poctivci a padouši: trojice – pracovní list + řešení
Bludiště a hledání cest
Bludiště jsou tvořena spletí chodeb a cest, ve kterých typicky hledáme cestu od startu k cíli. Lidé jsou bludišti fascinováni již od dávných dob. Historicky známá bludiště zahrnují například legendární Minotaurovo bludiště z řecké mytologie nebo bludiště v zámeckých zahradách (např. slavné bludiště v Hampton Court v Anglii).
Bludiště slouží nejen k zábavě, ale také k rozvoji informatického a algoritmického myšlení. Řešení bludišť vyžaduje schopnost logického myšlení, plánování a strategického rozhodování, což jsou klíčové dovednosti pro programování a řešení složitějších algoritmických problémů.
Kromě níže uvedených interaktivních úloh jsou k dispozici i následující pracovní listy na vytištění:
NahoruPlánování
V těchto úlohách si procvičíte schopnost najít posloupnost kroků k dosažení požadovaného stavu.
Nahoru