Výpis souhrnů
Práce s daty
Podtémata
- Práce s daty
- Sběr a evidence dat
- Získávání dat
- Zápis dat do tabulky
- Vyjádření informací slovně a číslem
- Formát dat
- Zkreslení dat
- Základy práce s daty
- Tabulky: základní porozumění
- Řazení dat
- Řazení dat v tabulkách
- Vztahy grafů a tabulek
- Vizualizace dat: principy
- Vizuální kódování dat
- Součásti grafů, pojmy
- Nevhodné vizualizace a jejich úpravy
- Vizualizace dat: typy grafů
- Rozlišování typů grafů
- Sloupcové grafy
- Sloupcové grafy: základní
- Sloupcové grafy: skupinové a skládané
- Koláčové grafy
- Spojnicové grafy
- Bodové grafy
- Plošné grafy
- Histogramy
- Tabulkový editor
- Tabulky: buňky, řádky, sloupce
- Tabulky: početní operace
- Tabulky: rozsahy
- Tabulky: odkazy
- Tabulky: funkce
- Tabulky: podmínky
- Databáze
- Použití databází
- Relační databáze
- SQL: základy
- Entitně-vztahové modely
- Regulární výrazy
- Základní vyhledávání
- Skupiny znaků
- Kvantifikátory
- Hranice
Práce s daty
Data jsou údaje, které popisují svět kolem nás. Získáváme je třeba pozorováním nebo měřením. Data můžeme evidovat a analyzovat i na papíře (dříve se to tak běžně dělalo). Dnes pro práci s daty většinou používáme počítače a data ukládáme třeba pomocí tabulkového editoru nebo databází.
Data jsou nejčastěji číselná (čas běhu při závodech, počet hlasů ve volbách, cena výrobku, počet obyvatel), ale mohou být i textová (jméno studenta, oblíbená barva, název státu).
V rámci členíme toto téma na několik podtémat:
- Sběr a evidence dat – Porozumění tomu, jakou podobu data mohou mít a jak je získávat.
- Základy práce s daty – Základní úkony při práci s daty, jejich vyčítání z tabulek, řazení a znázorňování pomocí tabulek a grafů.
- Vizualizace dat: principy – Pomocí vizualizací můžeme datům daleko snáz porozumět. Pro přípravu dobrých vizualizací potřebujeme rozumět jejich základním principům.
- Vizualizace dat: typy grafů – Přehled typů grafů, které často používáme pro vizualizace, a jejich použití.
- Tabulkový editor – Základní způsob zpracování dat na počítači nabízí tabulkové editory (např. Microsoft Excel, Google Sheets, LibreOffice Calc).
Krom těchto základních témat jsou k dispozici i dvě pokročilejší témata:
- Databáze – Rozsáhlá data ukládáme do databází a pracujeme s nimi pomocí specializovaných programovacích jazyků jako je SQL.
- Regulární výrazy – Při práci s textovými daty často využíváme regulární výrazy, které umožňují popisovat vzory v textu.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 4.–6. ročník | Úplné základy práce s daty, zápis dat do tabulky, řazení, sloupcové grafy. | |
| 5.–7. ročník | Základy práce s tabulkovým editorem. | |
| 7.–9. ročník | Zpracování dat pomocí tabulkového editoru. | |
| 7.–9. ročník | Vizualizace dat pomocí grafů, základní principy vizualizace, nevhodné vizualizace. | |
| 1.–4. ročník SŠ | Zpracování dat pomocí tabulek a vizualizací, základní znalosti z oblasti databází. |
Pracovní listy
Kromě níže uvedených interaktivních cvičení jsou k dispozici také následující pracovní listy, které vždy zobrazují graf vycházející z reálných dat a k němu několik úkolů:
Sběr a evidence dat
Abychom mohli s daty pracovat a provádět s nimi analýzy, musíme je nejdříve získat a přehledně zaznamenat. Toho se týká několik podtémat:
- Získávání dat – pozorování, měření, využití dotazníků, získání a zpracování dat z existujících zdrojů
- Zápis dat do tabulky – zachycení tabulkou usnadňuje jak sběr, tak následnou práci s daty
- Vyjádření informací slovně a číslem – některá data vyjadřujeme číslem (např. výška, rok narození), jiná slovně (např. barva očí, oblíbená zmrzlina)
- Formát dat – některé informace (např. časové údaje) můžeme zapisovat různými formáty
- Zkreslení dat – posbíraná data nejsou nutně věrným obrazem skutečnosti, mohou trpět různými zkresleními
Získávání dat
K získávání dat slouží například:
- pozorování – Využívá lidské smysly.
- měření – Výsledkem jsou číselné údaje, které lze porovnávat. Obvykle mají určitou jednotku (např. m, kg). Pro měření bývají často využívány přístroje. Měření může být podle způsobu provedení různě přesné.
- využití dotazníků – Zahrnuje získávání informací od většího množství lidí.
- analýza (zpracování, vyhodnocení) jiných dat
Získaná data lze zaznamenávat do digitálních zařízení, ale třeba i jednoduše na papír. Pokud sbíráme data o lidech, můžeme je spojit s identitou (např. jménem) určitého člověka, nebo je sbírat anonymně.
Různá data se získávají různě obtížně. Člověk zpravidla snáze bude získávat data, která se týkají skutečností v jeho okolí, data, která se týkají menšího množství lidí či data, k jejichž získání nejsou potřeba specializované přístroje.
Mnohá data byla již zjištěna a není nutné je získávat znovu. Stačí je vyhledat ve vhodném zdroji (např. počet obyvatel Brna v minulém roce zjistíme na webu ČSÚ). Již existující data ale nejsou vždy volně dostupná.
Při získávání i zpracování dat se mohou vyskytnout chyby či zkreslení. Zvláště při získávání/zpracování větších souborů dat se těmto jevům nelze zcela vyhnout, je však vhodné pokusit se jejich výskyt omezit.
NahoruZápis dat do tabulky
Abychom mohli s daty pracovat, musíme je nejdříve získat a přehledně zapsat. Základní způsob, jak si data o světě kolem nás udržovat, je použít tabulku. Některá data můžeme získat přímo v tabulkové podobě, například na Wikipedii lze najít řadu zajímavých tabulek o světě (třeba státy podle počtu obyvatel).
Co když chceme zpracovávat informace ze svého okolí? Například data o tom, jaká domácí zvířata mají doma spolužáci, na Wikipedii nenajdeme. Můžeme si ale vyrobit vlastní tabulku.
NahoruVyjádření informací slovně a číslem
Vyjádření číslem
Čísly vyjadřujeme např. počty, pořadí, či hodnoty veličin (v kombinaci s jednotkou). Informace v podobě čísla jsou obvykle přesné, lze je řadit, provádět s nimi početní operace či je statisticky vyhodnocovat.
Příklady informací vyjádřených čísly:
- Můj bratr se narodil v roce 2023.
- Eva má 2 morčata.
- Jakub skončil na 3. místě.
- Představení začíná v 19.00 hodin.
- Kopretina bílá dorůstá výšky asi 0,5 m.
Vyjádření slovy
Mnohé informace se vyjadřují slovy či slovním popisem. Jedná se třeba o vlastnosti, pocity nebo dojmy. Slovní popis bývá zpravidla do určité míry subjektivní (závislý na pohledu autora), méně přesný než číslo.
Příklady informací vyjádřených slovy:
- Žofie má přátelskou povahu.
- Martin má hnědé oči.
- Hostující tým ve druhém poločasu obrátil skóre.
Porovnání
Konkrétní způsoby vyjádření informace mohou být výhodné v různých situacích, případně se mohou doplňovat.
| Slovně | Číslem | Komentář |
|---|---|---|
| Přidejte špetku soli. | Přidejte 0,4 g soli. | Slovní vyjádření je rychlejší, sůl obvykle nevážíme na desetiny gramu. |
| Petr má hodně pokojových rostlin. | Petr má 15 pokojových rostlin. | Pokud řekneme „hodně“, poskytne to základní přehled a není nutné znát konkrétní počet. |
| Přidávejte mouku, dokud těsto nezíská vláčnou konzistenci. | Nelze vyjádřit číslem. | |
| Film měl skvělé vizuální efekty, ale nezajímavý příběh. | 3/5 hvězdiček | Oba způsoby popisu se vhodně doplňují. |
| Ponorný tyčový mixér AppetitChef Turbo | katalogové číslo 1 334 751 | Název je přístupnější pro zákazníka, katalogové číslo produkt jednoznačně identifikuje. |
Formát dat
Data mohou mít různý formát. V základu mohou mít tvar textového řetězce (např. želva), čísla (např. 1) nebo logické hodnoty (TRUE – pravda, FALSE – nepravda).
Čísla mohou mít rozličnou podobu. Pokud 0 zastupuje číslici (respektive v některých případech celé číslo), můžeme získat například:
0,0– desetinné číslo000 000 000– telefonní číslo bez předvolby000 00– poštovní směrovací číslo0/0– zlomek0 %– procento0 m– vzdálenost v metrech
Specifické je formátování času. Uvažme, že Y zastupuje rok, m měsíc, d den, H hodinu, M minutu a S sekundu. V rámci tohoto formátu získáme například:
H.M– čas v rámci dne, uplynulé hodiny a minutyM:S– uplynulé minuty a sekundyd. m. Y– datum (formát typický pro češtinu)m/d/Y– datum (formát typický pro americkou angličtinu)
Zástupné znaky (jako výše) se pro formátování dat používají např. v rámci programovacích jazyků či tabulkového procesoru. Na podobném principu fungují regulární výrazy, které se používají hlavně pro vyhledávání v datech.
Využít konkrétní formát (či kontrolu) dat je výhodné třeba v dotaznících: pokud chceme od respondenta získat PSČ, hodí se vstup omezit pouze na 5 číslic. Zamezíme tak zadání chybných dat.
NahoruZkreslení dat
Při práci s daty se může snadno stát, že dostupná data jsou nějakým způsobem zkreslená. Taková data pak nevypovídají dobře o skutečnosti. Pokud zkreslení nevezmeme v úvahu, může zpracování takových dat vést k matoucím závěrům. Je proto užitečné základní typy zkreslení znát.
Výběrové zkreslení
Při sběru dat většinou není reálné posbírat „všechna data“, často používáme jen nějaký výběr. Tento výběr by měl ideálně představovat takzvaný reprezentativní vzorek, který dobře odpovídá charakteristikám zkoumaného celku. Pokud tomu tak není, tak jsou data zkreslená.
Příklady nereprezentativních vzorků
- Průzkum názorů na politiku, který agentura provede pouze v Praze na náměstí.
- Výzkum účinků léku, do kterého jsou zapojeni pouze studenti sportovního gymnázia.
K tomuto typu zkreslení může dojít například tak, že se účastníci průzkumu sami rozhodují, zda se zúčastní či nikoliv (zkreslení neúčasti). Ti, kteří se rozhodnou neúčastnit, se často liší v důležitých ohledech od těch, kteří se účastní. Příklad: Dotazník o počítačových hrách vyplní s větší šancí ti, kdo rádi hrají počítačové hry.
Na výběrovém zkreslení se může podílet také množství získaných dat. Příklad: Když budeme zjišťovat zpětnou vazbu k výuce pouze u 2 žáků, pravděpodobně to nebude vypovídat o celé třídě.
Zkreslení odpovědí
Pokud sbíráme odpovědi dotazníkovým šetřením, může se stát z různých důvodů stát, že poskytnuté odpovědi neodpovídají přesně realitě. Účastníci výzkumu například mohou upravovat své odpovědi podle společenských očekávání či mohou odpovídat nepřesně, protože si přesnou odpověď nedovedou vybavit. Odpovědi mohou ovlivnit také takové detaily, jako je pořadí odpovědí v dotazníku.
Příklady zkreslení odpovědí
- Účastníci výzkumu o stravování mohou ve svých odpovědích přeceňovat konzumaci zdravých potravin nebo podceňovat příjem nezdravých potravin.
- Průzkum trávení času o loňských prázdninách může být zkreslen nepřesnými vzpomínkami.
Potvrzující zkreslení (konfirmační zkreslení)
Lidé mají přirozeně tendenci upřednostňovat informace, které podporují vlastní názory, a naopak ignorovat či podceňovat informace, které jsou s názory v rozporu. To se může přímo či nepřímo projevit i při sběru dat.
Příklad potvrzujícího zkreslení
- Výzkumník zkoumá vliv videoher na agresi.
- Má hypotézu, že videohry vedou k násilnému chování.
- Při průzkumu dostupných studií věnuje větší pozornost sběru a analýze dat odpovídajích jeho hypotéze.
Publikační zkreslení
K publikačnímu zkreslení dochází, když výsledek experimentu či analýzy ovlivňuje rozhodnutí, zda data publikovat nebo jinak šířit.
Příklad publikačního zkreslení
V lékařském výzkumu mohou farmaceutické společnosti rozhodnout o publikování pouze studií, které prokazují pozitivní výsledky nového léku, zatímco utají nebo nepublikují studie s nepříznivými výsledky. Toto zkreslení zpráv může vést k nadhodnocení účinnosti léku a zastření potenciálních rizik nebo vedlejších účinků.
Základy práce s daty
Hlavním prostředkem pro práci s daty jsou tabulky. S těmi na počítači pracujeme například v tabulkovém editoru. Nejdříve se však hodí procvičit si úplné základy s jednoduchými tabulkami, které bychom klidně mohli používat i na papíře.
| téma | obsah |
|---|---|
| Tabulky: základní porozumění | porozumění jednoduchým, malým tabulkám |
| Řazení dat | řazení podle různých kritérií (např. velikost čísel, abecední řazení), řazení vzestupně a sestupně |
| Řazení dat v tabulkách | řazení tabulek podle sloupců |
| Vztahy grafů a tabulek | vztah mezi tabulkou a její vizualizací, především pomocí sloupcového a koláčového grafu |
Tabulky: základní porozumění
Základem práce s daty jsou tabulky. S tabulkami můžeme na počítači pracovat v tabulkovém editoru, vykreslovat podle nich grafy, nebo je ukládat do databází. Ale před tím, než se do těchto činností pustíme, musíme rozumět prosté tabulce, kterou máme třeba před sebou na papíře.
NahoruŘazení dat
Velice užitečnou pomůckou pro lepší přehlednost dat je řazení. Když si data seřadíme, snadno vidíme největší a nejmenší hodnoty. Také si třeba všimneme rozestupů mezi jednotlivými záznamy či zajímavých pravidelností.
Data mohou být seřazena:
- vzestupně – Od nejmenších čísel po největší, od dřívějšího data (času) po pozdější, od A do Z. Mějme např. čísla 4, 10, 2, 9. Seřadíme-li je vzestupně, dostaneme 2, 4, 9, 10.
- sestupně – Od největších čísel po nejmenší, od pozdějšího data (času) ke dřívějšímu, od Z do A. Mějme např. jména Linda, Jirka, Aneta, Vincent. Seřadíme-li je od Z do A (sestupně), dostaneme Vincent, Linda, Jirka, Aneta.
Řazení dat v tabulkách
Pro práci s daty se často využívají tabulky, v nichž lze tato data různě řadit. Uvažme třeba následující tabulku evidující data o tom, kolik má kdo z kamarádů rybiček:
| jméno | příjmení | počet rybiček |
|---|---|---|
| Linda | Veselá | 3 |
| Jirka | Novák | 0 |
| Aneta | Procházková | 12 |
| Vincent | Černý | 5 |
Data v tabulkách se obvykle řadí podle určitých sloupců. Pokud má tabulka záhlaví (tedy první řádek, který říká, jaká data budou následovat), záhlaví při řazení zůstává na svém místě. Řadí se jen data, která se k němu vztahují.
Použijeme-li vzestupné řazení podle příjmení, dostaneme kamarády v tomto pořadí:
| jméno | příjmení | počet rybiček |
|---|---|---|
| Vincent | Černý | 5 |
| Jirka | Novák | 0 |
| Aneta | Procházková | 12 |
| Linda | Veselá | 3 |
Všimněte si, že společně s příjmeními jsme vždy seřadili i související data v řádcích (jméno, počet rybiček). Pokud bychom řadili samotný sloupec s příjmením, data by se nám „pomíchala“:
| jméno | příjmení | počet rybiček |
|---|---|---|
| Linda | Černý | 3 |
| Jirka | Novák | 0 |
| Aneta | Veselá | 12 |
| Vincent | Procházková | 5 |
Vztahy grafů a tabulek
Data často zaznamenáváme do tabulek, ale pro lepší porozumění je pak znázorňujeme graficky. S grafickým znázorněním dat se můžeme často setkat například i v médiích nebo reklamních materiálech. Pro jakoukoliv práci s daty je potřeba rozumět oběma těmto způsobům znázornění dat a umět mezi nimi přecházet.
NahoruVizualizace dat: principy
Vizualizace dat nám umožňuje přehledně zobrazit informace a lépe porozumět číslům a vztahům mezi nimi. Dobře navržený graf dokáže rychle sdělit podstatné informace, avšak špatně zvolená vizualizace může být nepřehledná, nebo dokonce zavádějící. Proto je důležité znát základní principy, jak data ve vizuální podobě správně zobrazovat.
- Vizuální kódování dat – způsoby, jak data převádíme do vizuální podoby: pomocí délky, polohy, velikosti, úhlu, barvy nebo odstínu
- Součásti grafů, pojmy – základní části grafu: nadpis, osy, popisky, legenda, mřížka a datové řady
- Nevhodné vizualizace a jejich úpravy – přehled častých chyb ve vizualizacích a cvičení na jejich odhalování (např. nevhodné 3D efekty, špatně zvolené osy)
Detailnější rozbor konkrétních způsobů vizualizace dat je pak uveden v tématu Vizualizace dat: typy grafů.
NahoruVizuální kódování dat
Řekněme, že jsme posbírali data a máme je zapsaná v tabulce. Abychom jim lépe porozuměli, je užitečné je vizualizovat, tj. zobrazit formou obrázku. To můžeme udělat mnoha způsoby. Například následující obrázek ukazuje několik způsobů znázornění stejných dat (A → 5, B → 2, C → 4).

Způsob ztvárnění volíme podle účelu vizualizace. Pokud chceme být schopni hodnoty snadno porovnávat, použijeme délku nebo polohu bodů, protože velikosti ploch, úhly a barvy se lidem srovnávají hůře. Pokud ale chceme být schopni rychle odhadnout, jak velkou část z celku něco tvoří, je většinou výhodnější použít úhly.
Můžeme též různé způsoby znázornění kombinovat. Například následující vizualizace zobrazuje délku života mužů a žen v různých státech světa. Klíčová informace o délce života je kódována pomocí polohy bodů, což usnadňuje srovnání států. Velikost a barva bodů pak zobrazují doplňkové informace (velikost států a příslušnost ke kontinentu).
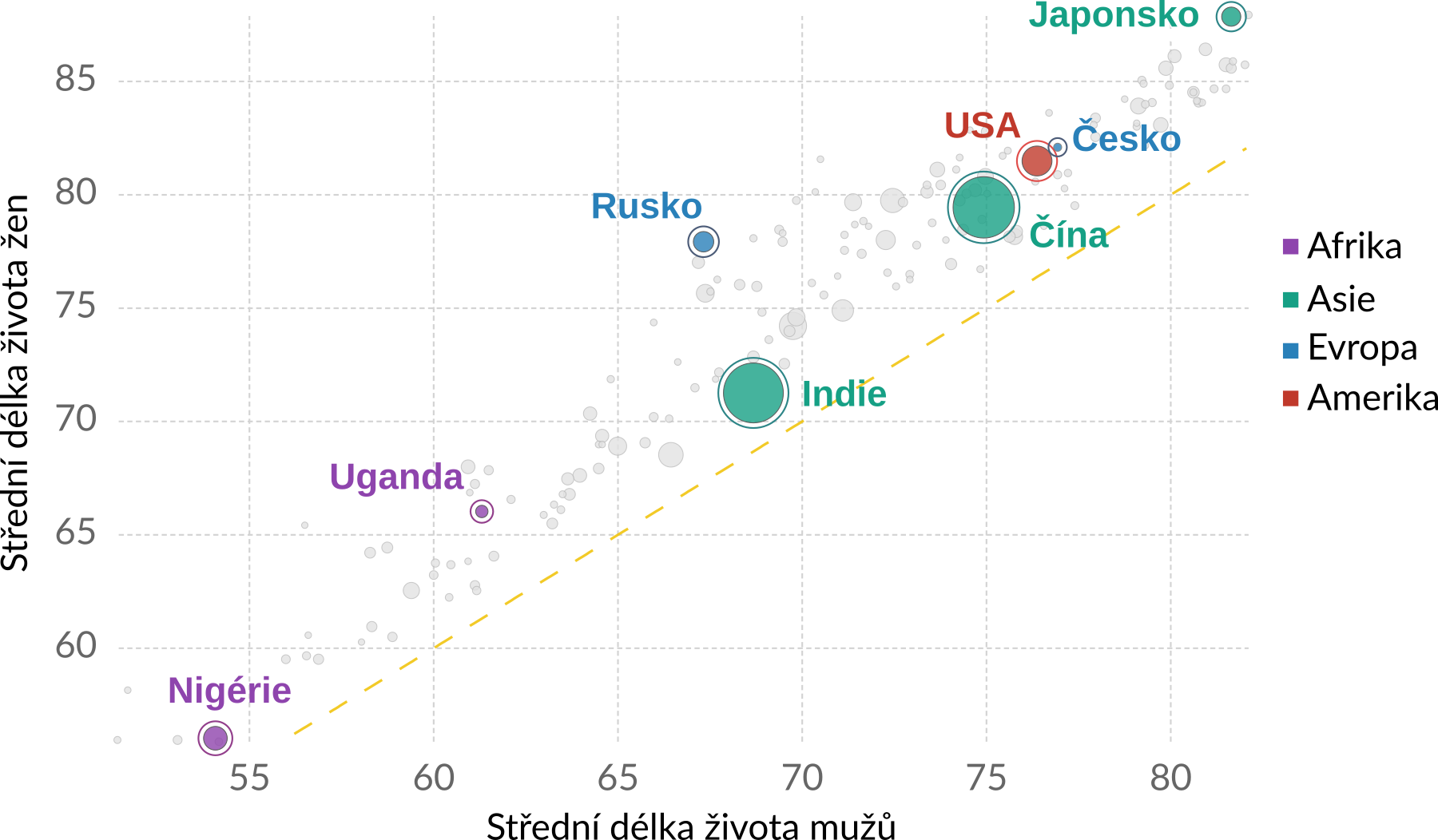
Zdroj obrázku: Our World in Data
NahoruSoučásti grafů, pojmy
Grafy sestávají z jednotlivých součástí, které se obvykle ztvárňují a uspořádávají podle určitých pravidel. Díky tomu je možné se snadněji orientovat v různých grafech. Čtenář může bez váhání rozeznat, co která součást grafu vyjadřuje.
Grafy zpravidla mívají nadpis, který stručně shrnuje data v grafu.
U grafů, které vyznačují data pomocí vzdáleností (sloupcové, spojnicové, bodové), jsou základní součástí osy. Svislá osa směřuje odshora dolů, také se označuje jako osa y. Vodorovná osa směřuje zleva doprava, také se označuje jako osa x. V souvislosti s osami může být uveden jak název samotné osy (co která osa značí), tak popisy hodnot/kategorií.
Datové řady jsou řádky či sloupce tabulky obsahující data, která graf znázorňuje. Data mohou být v grafu vyznačena např. pomocí sloupců či bodů (mezi těmi mohou být spojnice).
Mřížka usnadňuje orientaci v oblasti se znázorněnými daty. Mezi úsečkami hlavní mřížky bývají větší vzdálenosti, oblast grafu je jemněji dělena (zpravidla méně výraznou) vedlejší mřížkou.
U grafů může být přítomna spojnice trendu (anglicky trendline), která vyjadřuje odhad postupného vývoje hodnot.
Legenda popisuje, kterých dat se týká určitá datová řada či výseč. Často spojuje název určité kategorie dat s barvou či grafickým vzorkem.
U koláčových (výsečových) grafů bývá přítomen nadpis, samotné výseče s případnými textově vyjádřenými hodnotami dat a legenda.
NahoruNevhodné vizualizace a jejich úpravy
Grafy by měly data prezentovat přehledně a jasně. V souvislosti s tím je potřeba dodržovat určité zásady jejich ztvárňování a vyhnout se typickým chybám.
Součásti grafů a jejich umístění
Grafy by měly obsahovat všechny odpovídající součásti, zejména popisy hodnot/kategorií. U sloupcových, bodových či plošných grafů by obvykle neměly chybět názvy (popisy) os. Pokud do grafu zahrneme nadpis, měl by jasně shrnovat, co graf ukazuje.
Číselné hodnoty by měly mít správný formát (např. vhodný počet desetinných míst), případně uvedenou jednotku.
Součásti grafů by měly být rozmístěné tak, aby se navzájem nepřekrývaly.
3D zobrazení
Trojrozměrné zobrazení může na první pohled vypadat lákavě, obecně jej však není vhodné používat. U „3D“ sloupců není jasné, kam až dosahují. U trojrozměrně provedeného výsečového (koláčového) grafu kategorie umístěné „vpředu“ působí jako větší (toho se někdy využívá i při manipulaci čtenáře).
Odpovídající množství kategorií
Grafy by neměly obsahovat nadměrné množství kategorií (typicky u výsečových grafů). Mnoho dat je lepší rozdělit do více grafů.
Manipulace s osami
Osy by měly (obvykle) začínat na hodnotě 0. „Podtržení“ osy (osa začíná na vyšší hodnotě) se opět může používat k manipulaci. Pokud např. bude svislá osa začínat na 10 000 Kč, 12 000 Kč bude zdánlivě působit jako „dvojnásobek“ 11 000 Kč.
Použití barev
V grafech obvykle není potřeba používat mnoho barev (např. zvláštní barvu pro každou kategorii v jednoduchém sloupcovém grafu).
Barvy by měly být voleny tak, aby šly dostatečně dobře rozlišit (např. nevybrat blízké odstíny modré, pro osoby s poruchou barvocitu není vhodné kombinovat červenou a zelenou).
Také je nutné brát ohled na médium, pomocí něhož bude graf prezentován: např. pro černobílý tisk se budou hodit spíše různé vzory výplní.
Jednotnost
Pokud prezentujeme najednou více grafů, měly by být provedené jednotně (konzistentně).
NahoruVizualizace dat: typy grafů
Pojem „graf“ má bohužel v češtině několik odlišných významů. Mimo jiné máme grafy funkcí, grafy modelující vztahy mezi objekty a grafy znázorňující data. Zde se zabýváme posledním zmíněným významem.
- Sloupcové grafy typicky používáme pro znázornění hodnot pro několik kategorií (např. počet obyvatel pro jednotlivé státy). Data jsou vyjádřena jako sloupečky.
- Koláčové grafy využíváme především pro vyjádření „části z celku“ (např. jaká část lidí žije na jednotlivých kontinentech), mají blízký vztah k procentům. Data jsou vyjádřena jako výseče kruhu.
- Spojnicové grafy využíváme pro data, která jsou přirozeně uspořádána do posloupností, především pro data měnící se v čase (např. průměrná teplota v měsících). Data jsou vyjádřena pomocí lomených čar.
- Plošné grafy jsou podobné jako spojnicové, ale znázorňují hodnoty pomocí plochy.
- Bodové grafy využíváme pro vyjádření vztahu mezi dvěma veličinami (např. vztah mezi výškou a hmotností žáků ve třídě). Data jsou vyjádřena pomocí bodů.
- Histogramy vypadají podobně jako sloupcové grafy, používají se pro vyjádření rozložení hodnot spojité veličiny rozdělené do intervalů (např. rozložení hmotnosti v populaci).
Výše uvedené typy grafů je dobré umět rozlišovat. Též se hodí znát jednotlivé součásti grafů a jejich použití.
Pracovní listy
Kromě níže uvedených interaktivních cvičení jsou k dispozici také následující pracovní listy, které vždy zobrazují graf vycházející z reálných dat a k němu několik úkolů:
Rozlišování typů grafů
Pro různá data se hodí využít různé typy grafů. Základem jejich použití je znát jejich názvy, abychom je například našli v programu, který pro analýzu dat používáme.
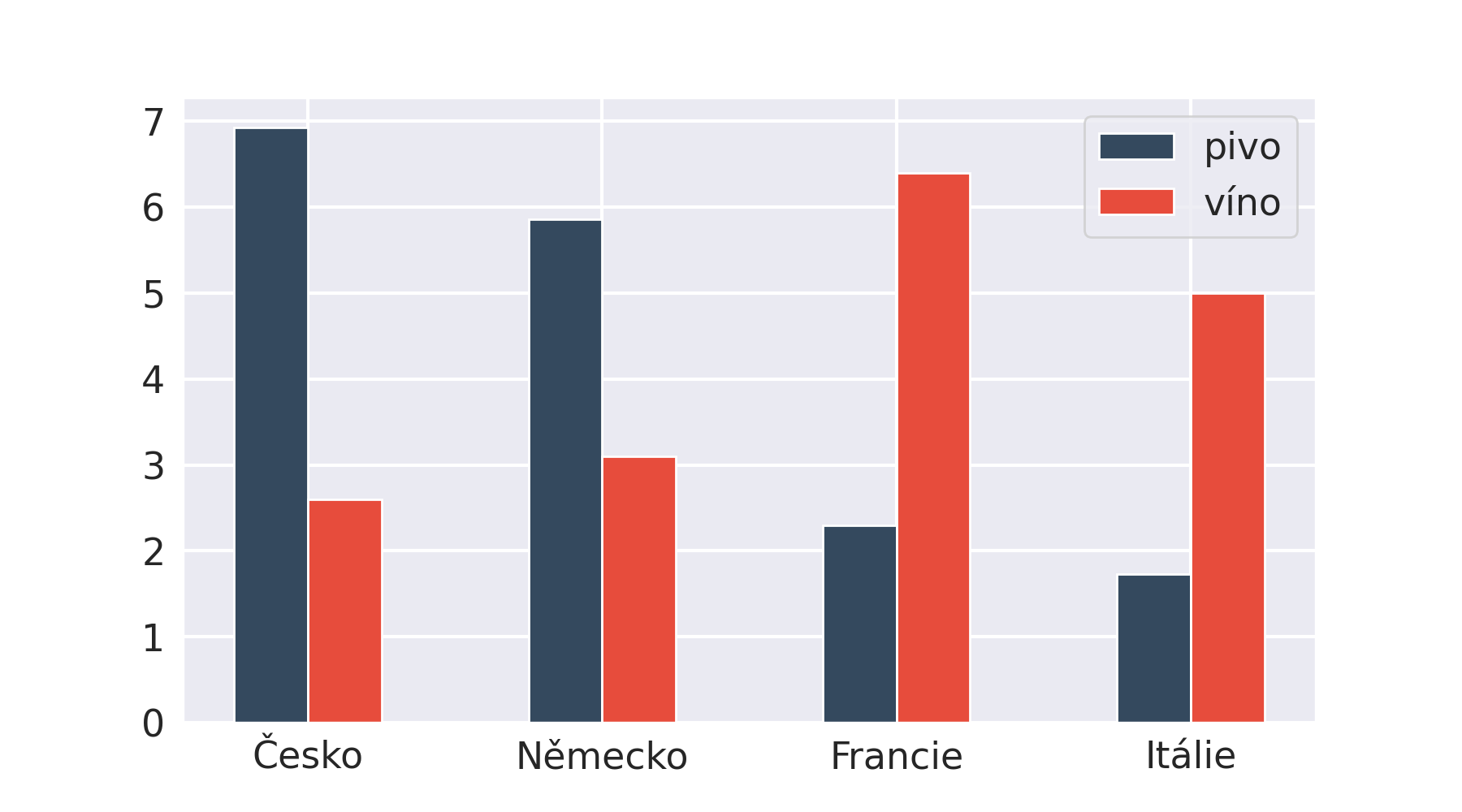
| Sloupcový graf Znázorňuje data pomocí obdélníků (sloupců), ty mohou být uspořádány svisle nebo vodorovně a uspořádány do skupin. |
 |
| Koláčový graf Vyznačuje část celku pomocí výsečí. Čím větší je určitá výseč, tím větší část celku znázorňuje. |
 |
| Spojnicový graf Zobrazuje data pomocí bodů, které jsou spojeny čárami. Používá se hlavně pro časové řady. |
 |
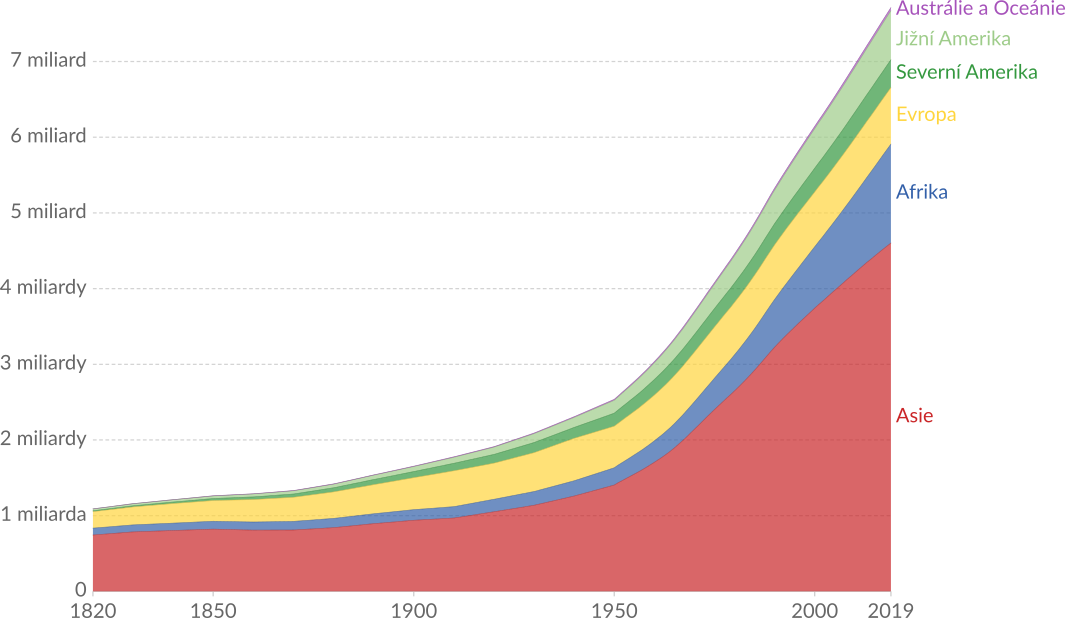
| Plošný graf Podobný jako spojnicový, ale znázorňuje hodnoty pomocí plochy. |
 |
| Bodový graf Popisuje vztah dvou proměnných skrze souřadnice bodů. |
 |
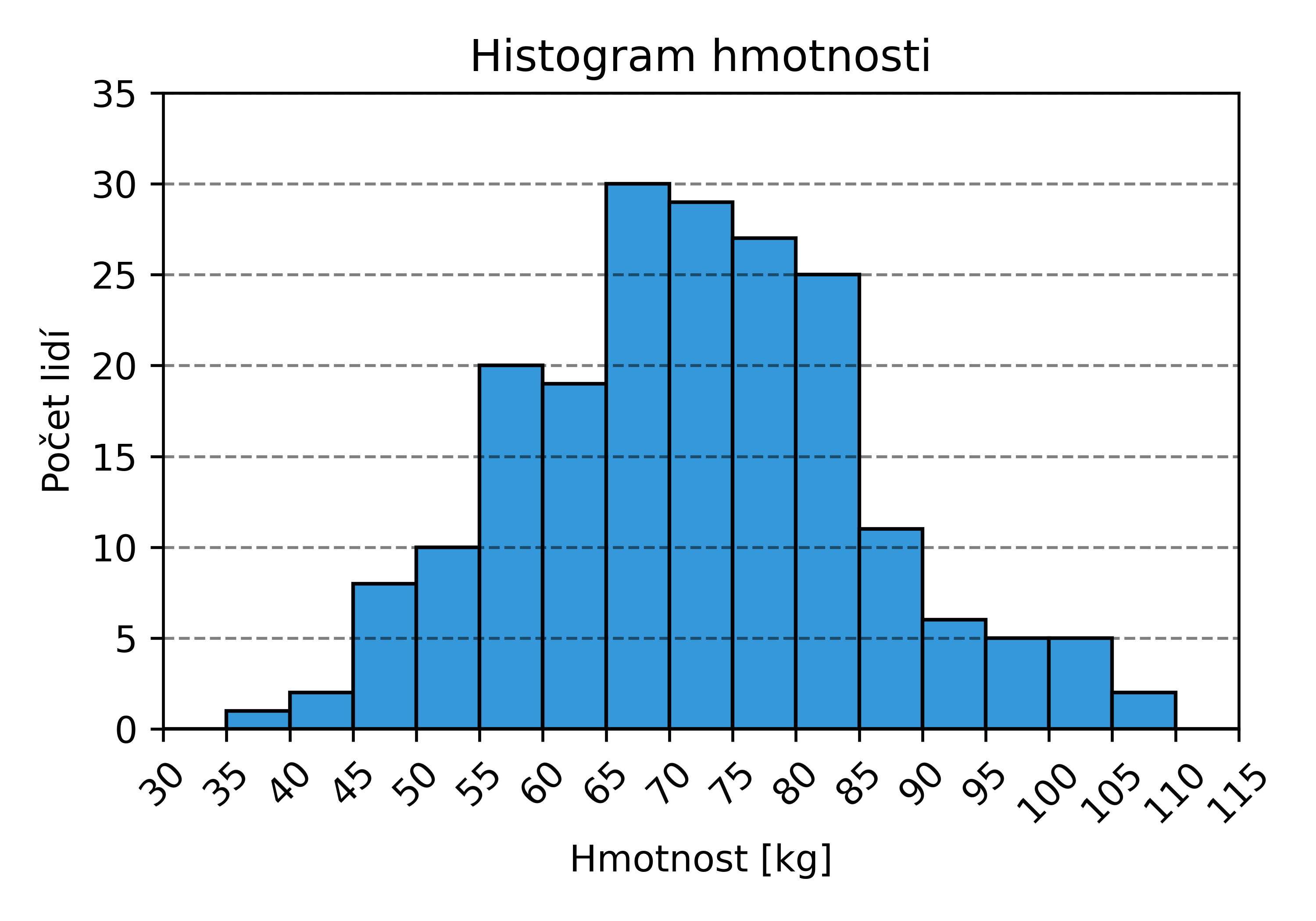
| Histogram Zobrazuje rozložení dat pomocí sloupců, jejichž výška odpovídá četnosti dat v daném intervalu. Na rozdíl od sloupcového grafu nejsou na vodorovné ose kategorie, ale spojitá proměnná (např. hmotnost). |
 |
| Krabicový graf Zobrazuje interval, ve kterém leží polovina dat, čára uvnitř obdélníku značí medián. Význam čar vycházejících z obdélníku se různí, mohou například zobrazovat maximální rozsah dat. |
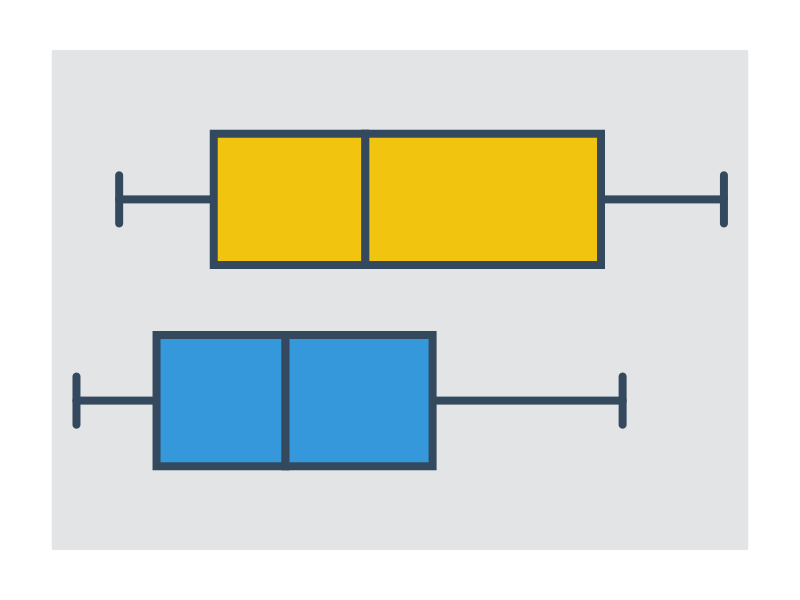 |
Sloupcové grafy
Sloupcový graf (bar chart) znázorňuje data pomocí obdélníků (sloupců), jejichž délka odpovídá hodnotě, kterou představují. Sloupce mohou být uspořádány svisle nebo vodorovně. Vodorovně uspořádané sloupcové grafy se také někdy označují jako řádkové či pruhové.
K dispozici jsou tato podtémata:
- Sloupcové grafy: základní – Procvičuje orientaci v grafech, které obsahují pro každou skupinu dat jen jednoduchý sloupec.
- Sloupcové grafy: skupinové a skládané – Složitější grafy, které pro určitou skupinu dat zobrazují více hodnot (sloupce vedle sebe či části sloupců nad sebou).
- Sloupcové grafy: mix
Sloupcové grafy: základní
Sloupcový graf (bar chart) znázorňuje data pomocí obdélníků (sloupců), jejichž délka odpovídá hodnotě, kterou představují. Sloupce mohou být uspořádány svisle (na ukázce vlevo) nebo vodorovně (na ukázce vpravo). Vodorovně uspořádané sloupcové grafy se také někdy označují jako řádkové či pruhové.


Typ zobrazených dat
Sloupcový graf se používá především pro vyjádření hodnot příslušných ke kategoriím (kategorickým datům).
| kategorická proměnná (jednotlivé sloupce) | příslušná hodnota (délka obdélníku) |
|---|---|
| nemoci | počty úmrtí |
| státy | rozlohy |
| města | počty obyvatel |
| sociální sítě | počty uživatelů |
Sloupcový graf většinou není vhodný pro zobrazení změn v čase, k tomu lépe slouží spojnicové grafy.
NahoruSloupcové grafy: skupinové a skládané
Skupinový sloupcový graf
Skupinový sloupcový graf (grouped bar chart, clustered bar chart) pro každou skupinu zobrazuje několik hodnot formou sloupců vedle sebe. Následující příklad pro každou zemi zobrazuje spotřebu zvlášť piva a vína (průměr na osobu a měsíc).

Skládaný sloupcový graf
Skládaný sloupcový graf (stacked bar chart) zobrazuje také pro každou skupinu několik hodnot, ale ty jsou poskládány nad sebe. Díky tomu můžeme snadno porovnávat jejich součet. Následující graf zobrazuje zisky medailí z olympiád. Medaile jsou rozděleny podle své hodnoty (zlato, stříbro, bronz), současně však snadno vidíme i celkové zisky.
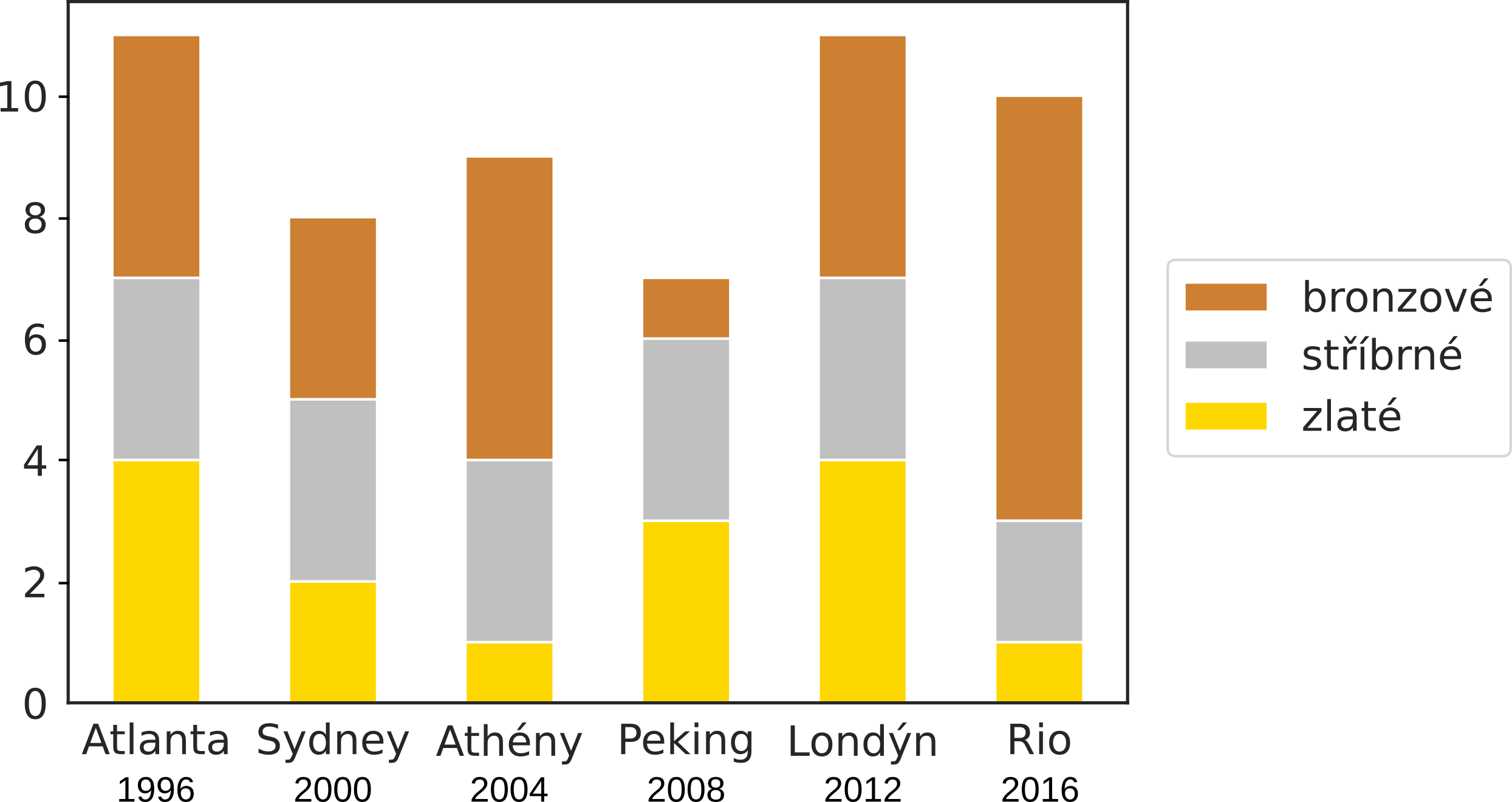
Pracovní list
K dispozici jsou následující materiály k vytištění:
NahoruKoláčové grafy
Koláčový graf (výsečový graf, kruhový diagram, anglicky pie chart) znázorňuje data formou kruhu rozděleného na sektory, přičemž velikost každého sektoru odpovídá podílu dané kategorie na celku. Tento typ grafu je vhodný pro vizualizaci procentuálního rozdělení nebo relativních četností různých kategorií v rámci jednoho datového souboru. Výseče mohou být popsané počty procent z celku nebo přímo hodnotami.
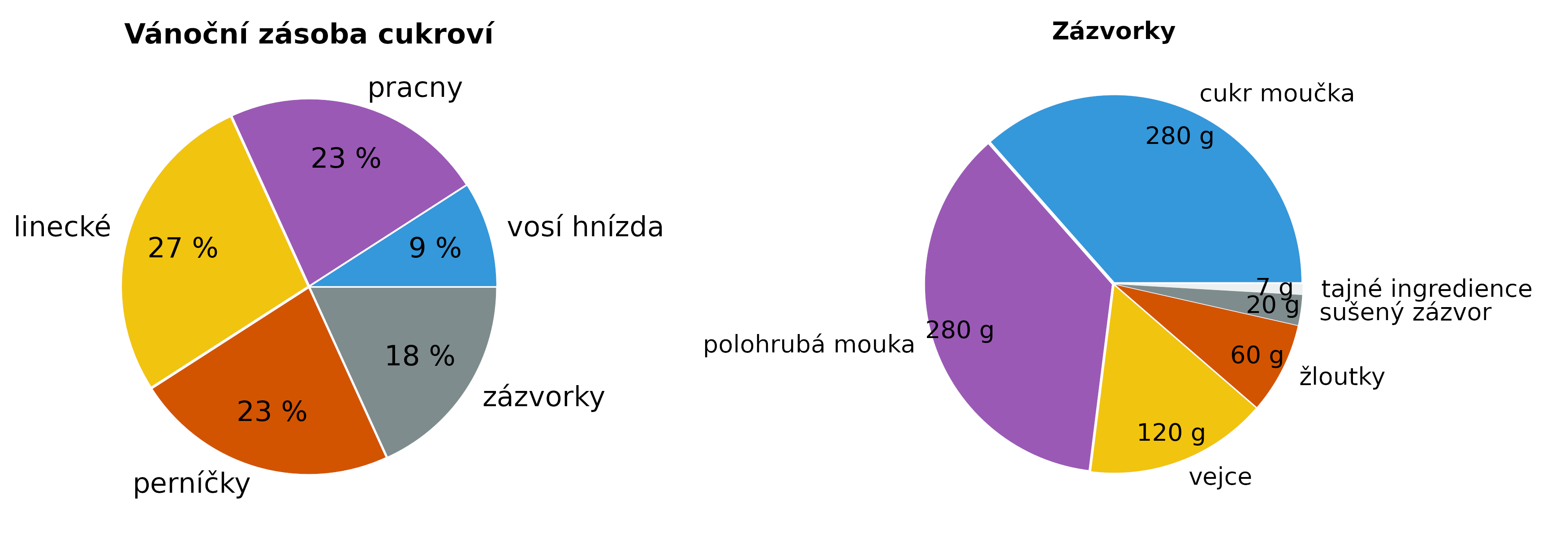
Koláčové grafy poskytují rychlou orientaci v celkovém složení. Například z uvedených ukázek na první pohled vidíme, že zázvorky jsou přibližně z třetiny tvořené cukrem a že polovinu vánoční zásoby cukroví tvoří linecké dohromady s perníčky.
Koláčový graf je nejčastěji používán pro zobrazení kategorických dat, kde lze snadno srovnávat relativní velikosti kategorií. Typická použití zahrnují zobrazení složení rozpočtu, populace či analýzu odpovědí v dotazníku.
Varianty grafu
Koblížkový graf (anglicky donut chart nebo doughnut chart) je variací koláčového grafu, kde je střed vyříznut a graf tak tvoří prstenec (název je odvozen od americké koblihy donut). Jde pouze o estetickou variaci, která má jinak stejné použití jako základní koláčový graf.
Vícevrstvý prstencový graf (v angličtině sunburst) má více vrstev zanořených prstenců. Jde o pokročilejší typ grafu, který je vhodný pro zobrazení hierarchických dat.
Nevhodná použití koláčového grafu
Koláčové grafy není vhodné kombinovat s 3D efekty a naklápěním. Takové zobrazení může vypadat atraktivně, ale vede ke zkreslení zobrazených dat. Vizualizace dat mají především věrně zobrazovat data.
Koláčové grafy nejsou vhodné pro srovnání přesných hodnot mezi kategoriemi nebo pro zobrazení malých rozdílů, protože odhad velikosti sektorů může být nepřesný. Také pokud máme více než 5-7 kategorií, koláčový graf se stává přeplněným a těžko čitelným. V těchto případech je vhodnější jej nahradit sloupcovým grafem.
Koláčové grafy nejsou vhodné pro zobrazení změn v čase. Pro takové účely je lepší použít spojnicové grafy, které poskytují jasnější vizualizaci trendů.
Pracovní list
Kromě níže uvedených interaktivních cvičení je k dispozici také materiál na vytištění:
NahoruSpojnicové grafy
Spojnicový graf (liniový graf, anglicky line chart) zobrazuje data pomocí bodů, které jsou spojeny čárami. Tento typ grafu dává smysl pro data, která jsou přirozeně uspořádána do posloupností.
Typické použití spojnicových grafů je pro zobrazení časových řad. Můžeme je však použít i v jiných případech, například pro zobrazení průběhu cyklistického závodu, kde osa x představuje vzdálenost od startu a osa y nadmořskou výšku.
Varianty grafu
Spojnicový graf může obsahovat více datových řad, přičemž každá může mít svůj vlastní popisek osy y. Toto zobrazení může být někdy méně přehledné, ale poskytuje možnost detailního srovnání různých datových sad.
Variací spojnicového grafu je plošný graf, ve kterém jsou oblasti mezi čarami vyplněny barvou. Plošné grafy jsou vhodné pro zobrazení kumulativních hodnot, jako jsou celkové výnosy firmy nebo celková spotřeba energie v průběhu času.
Nevhodná použití spojnicového grafu
Volba rozsahu osy y je klíčová. Obvykle by měla začínat od nuly, protože jinak může být vyznění grafu matoucí – může naznačovat výrazné trendy tam, kde nejsou. Toto pravidlo však není univerzální. To ostatně ukazuje výše uvedený příklad s teplotou, kde by nebylo vhodné, aby graf začínal od nuly.
Pokud nejsou prvky v zobrazované řadě pravidelně rozmístěny (např. máme data pro leden, únor, červen a prosinec), mělo by použité zobrazení správně odpovídat rozestupům. Pokud toto nezohledníme, může být graf zavádějící.
Pokud data nejsou přirozeně seřazena, je použití spojnicového grafu většinou nevhodné. Graf v takovém případě může vytvářet dojem kontinuity tam, kde žádná není. Například pokud máme data o výšce žáků ve třídě, zobrazení pomocí spojnicového grafu bude obsahovat spojnice, které neodpovídají žádným relevantním trendům. V takových případech je většinou vhodnější použít sloupcové grafy.
Pracovní list
Kromě níže uvedených interaktivních cvičení jsou k dispozici také materiály na vytištění:
NahoruBodové grafy
Bodový graf (anglicky scatter plot) znázorňuje hodnoty dvou proměnných vztahujících se ke stejnému objektu. Například následující graf zobrazuje průměrnou teplotu v lednu a červnu pro různá evropská města.
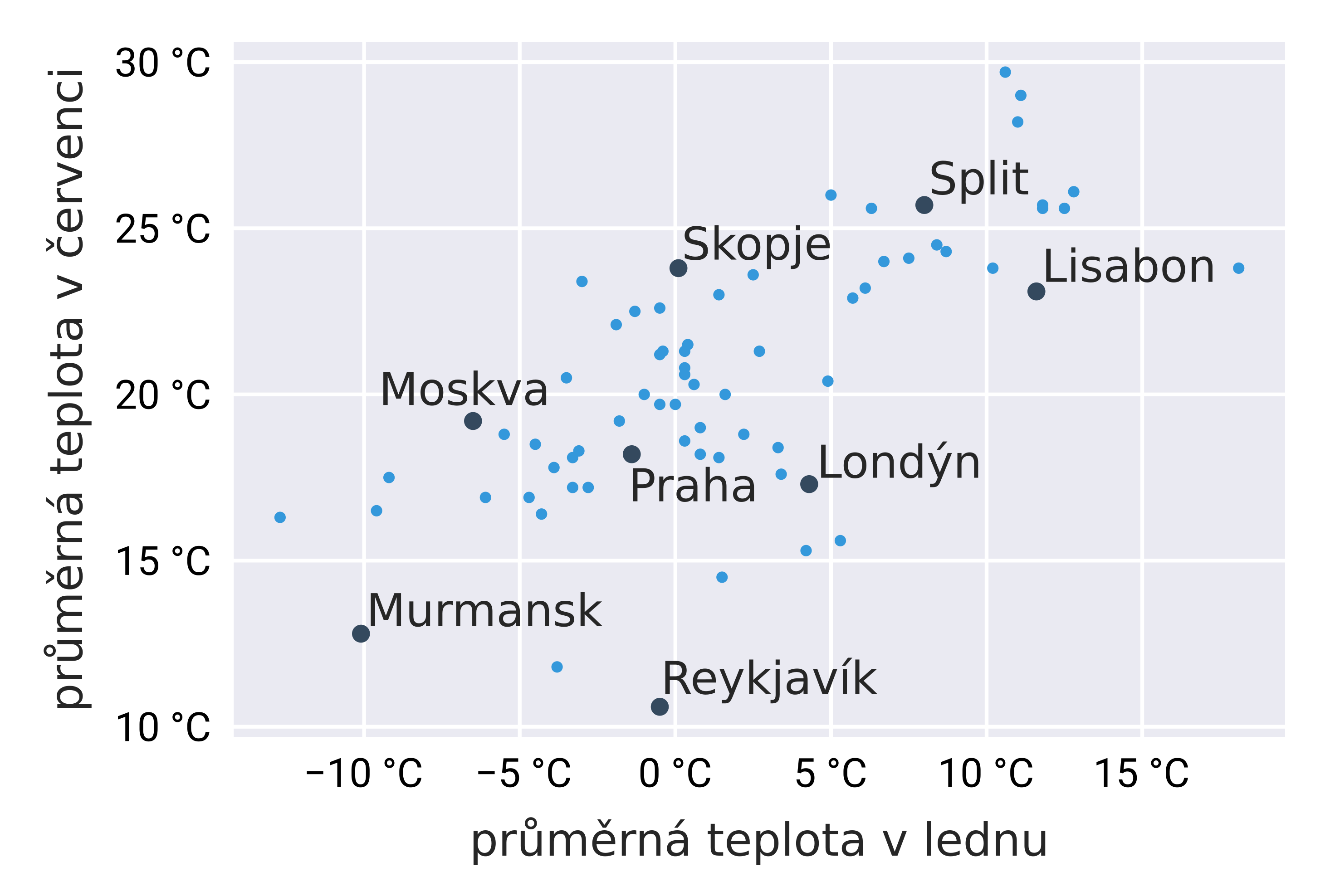
Bodový graf může zobrazovat informace i o dalších proměnných pomocí různých ztvárnění bodů. Například následující graf ukazuje pro státy světa dvě hlavní proměnné: střední délku života mužů a střední délku života žen. Tyto proměnné určují polohu bodů. Kromě toho graf ještě zobrazuje velikost populace jednotlivých států (velikost bodů) a jejich příslušnost ke kontinentům (barva bodů).

Varianta bodového grafu s různě velkými body se někdy nazývá bublinový graf (bubble chart).
Pracovní list
Kromě níže uvedených interaktivních cvičení jsou k dispozici také materiály na vytištění:
NahoruPlošné grafy
Plošný graf (anglicky area chart) je podobný jako spojnicový graf a také se typicky využívá pro zobrazení časových řad. V plošném grafu jsou oblasti mezi křivkami vyplněny barvou nebo vzorkem.
Plošné grafy se využívají především pro zobrazení kumulativních hodnot – součtů z několika kategorií. Následující příklad zobrazuje změny v počtu obyvatel na jednotlivých kontinentech. Plochy pro jednotlivé kontinenty jsou naskládány na sobě a v grafu tedy snadno vidíme i celkovou velikost populace na celém světě.

Dalšími příklady využití plošných grafů jsou zobrazení výnosů firmy z různých produktů nebo změny ve složení emisí skleníkových plynů.
NahoruHistogramy
Histogram znázorňuje počet výskytů různých hodnot sledované veličiny a často se používá, pokud měříme stejnou veličinu pro různé subjekty nebo v různých časech. Například následující histogram ukazuje hmotnost 200 různých lidí:

Měřená veličina (hmotnost) je rozdělena do několika intervalů, přičemž každý interval je reprezentován sloupcem. Výška sloupce ukazuje, kolikrát změřená hodnota padla do daného intervalu. Graf ukazuje, že hmotnost mezi 65 a 70 kg má právě 30 lidí.
Volba šířky intervalů
Důležitou volbou při tvorbě histogramů je velikost intervalů. Příliš široké intervaly mohou skrýt důležité rozdíly, protože odlišná pozorování shromáždí do stejného intervalu. Použití příliš úzkých intervalů naopak znamená, že v každém bude příliš málo pozorování, a vynikne statistický šum.
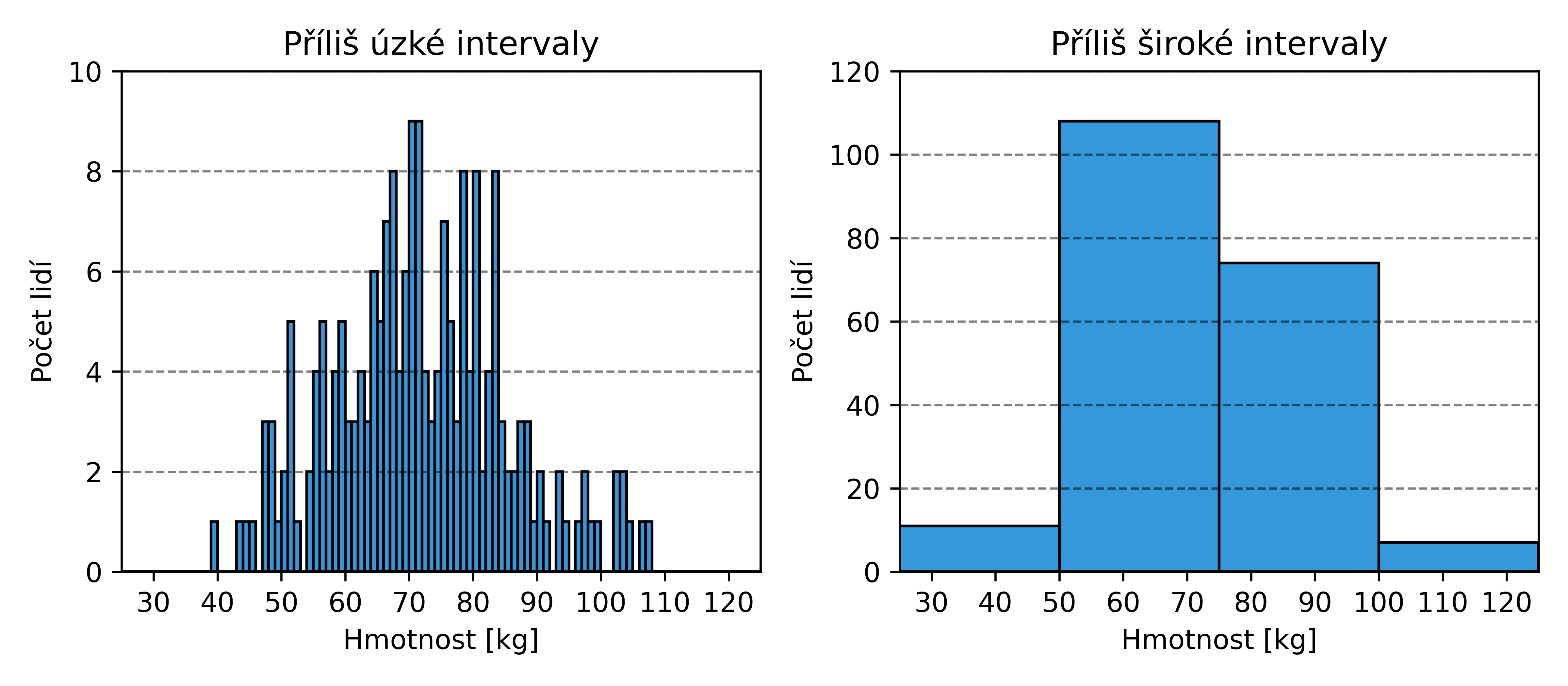
Histogramy s více třídami
Pokud je v datové sadě zastoupeno několik různých tříd (např. muži a ženy), je možné histogramy pro obě třídy překrýt, aby lépe vynikly rozdíly mezi těmito třídami. Následující histogram ukazuje, že ženy jsou zpravidla menší než muži, ale existuje i značný překryv – nejvyšší ženy jsou větší než nejmenší muži.
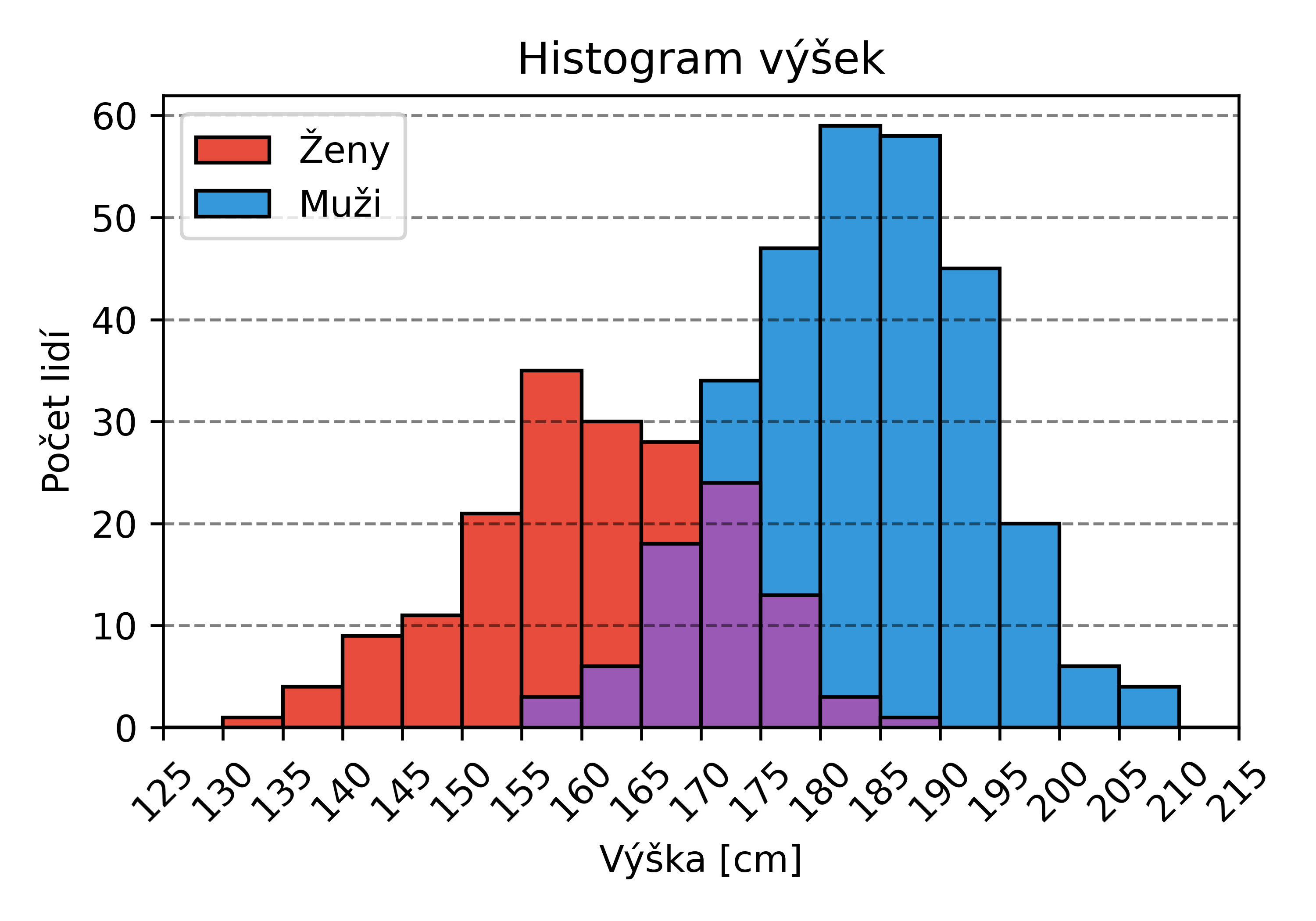
Použití histogramů
Histogramy umožňují rychle identifikovat nejčastější nebo naopak neobvyklé hodnoty. Používají se také jako odhad rozložení pravděpodobnosti. V takovém případě jsou místo počtů výskytů na ose y relativní četnosti v procentech.
Věkové pyramidy
Speciálním typem histogramu je věková pyramida, která ukazuje věkové rozložení populace. Měřená veličina (věk) bývá vynesena na svislé ose a šířka sloupců nalevo, resp. napravo od svislé osy ukazuje počet mužů/žen daného věku.
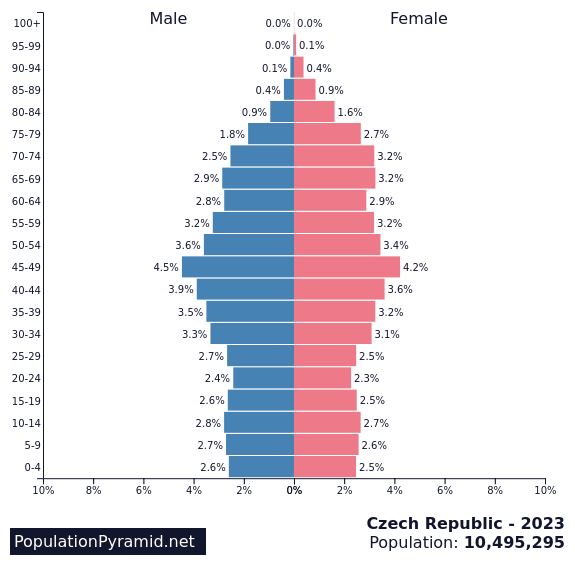
Histogramy vs. sloupcové grafy
Histogramy se podobají sloupcovým grafům, jen místo kategorických tříd sledují spojitou veličinu (např. hmotnost, výška, teplota, rychlost). Použitím intervalů uměle rozdělíme data do oddělených tříd, ty jsou ale stále seřaditelné. Občas se můžete setkat i s různě širokými intervaly v rámci jednoho grafu.
Tabulkový editor
Tabulkový editor (též tabulkový procesor, anglicky spreadsheet) je program pro zpracování tabulkových dat. Mezi známé tabulkové editory patří Microsoft Excel, LibreOffice Calc a Google Spreadsheets. Procvičování v není vázané na jeden konkrétní program, ale soustředí se na základní principy, které jsou společné všem těmto editorům:
- Buňky, řádky, sloupce – značení buněk v tabulce, základní orientace v tabulkách
- Ovládání tabulkového editoru – základní ovládací prvky tabulkového editoru
- Početní operace – zápis výpočtů v tabulkách, použití aritmetických operací (sčítání, odčítání, násobení, dělení)
- Rozsahy – vyjádření rozsahů v tabulkovém editoru, základ pro použití rozsahů v jednoduchých funkcích
- Odkazy – rozdíl mezi absolutním a relativním odkazem, jejich použití
- Funkce – použití funkcí pro součet, průměr, počet, zaokrouhlování a podobně
- Podmínky – použití podmínek v tabulkovém editoru
Tipy k procvičování tabulek v
- Rozhodovačka je vhodná pro úvodní seznámení s tématem nebo pro zopakování pojmů (např. po prodlevě v používání).
- Jako další krok je vhodné Přesouvání, které spočívá v doplňování chybějících dílčích částí do předpřipravené statické tabulky.
- Cvičení Tabulky je již založeno na plnohodnotné práci s tabulkovým editorem. Zadaná předpřipravená data si otevřete v libovolném tabulkovém editoru a máte za úkol zjistit z nich určitou informaci. Jaké bylo nejčastější křestní jméno dětí narozených v roce 1960?
Tabulky: buňky, řádky, sloupce
V listech tabulky v tabulkovém procesoru (editoru) jsou data uspořádaná do řádků a sloupců. Sloupce jsou označené písmeny (A, B, C…) a řádky čísly (1, 2, 3…). Každá buňka má tedy určitou pozici, kterou lze vyjádřit označením sloupce a řádku, v nichž se nachází. Například:
- A1 – Odkaz na obsah buňky ve sloupci
Aa v řádku1. - C10 – Odkaz na obsah buňky ve sloupci
Ca v řádku10.
Rozepsaný příklad: adresy buněk v tabulce
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | A1 | B1 | C1 | D1 | E1 | F1 |
| 2 | A2 | B2 | C2 | D2 | E2 | F2 |
| 3 | A3 | B3 | C3 | D3 | E3 | F3 |
| 4 | A4 | B4 | C4 | D4 | E4 | F4 |
Záhlaví (to se nachází zpravidla v prvním řádku) či první sloupec tabulky obvykle obsahují informace o tom, jaká data jsou obsažena v dalších řádcích či sloupcích.
Příklad tabulky se záhlavím: vymyšlení živočichové
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | oči | nohy | umí plavat | počet v bažině | |
| 2 | mažout | 5 | 9 | ano | 15 |
| 3 | pabuch | 6 | 5 | ne | 3 |
| 4 | slizolop | 9 | 3 | ano | 7 |
- V buňce
C1informace o tom, že ve sloupci následují počty nohou. - V buňce
A3je informace o tom, že v řádku budou následovat informace o pabuchovi. - Počet nohou pabucha je pak v buňce
C3.
Tabulky: početní operace
Tabulkový procesor lze využít k výpočtům. Vzorce vždy začínají znakem rovná se (=), tedy např. po zadání =5+2 do buňky se vypíše 7.
Základní početní operace se provádějí s použitím následujících znamének.
- sčítání: +
- odčítání: -
- násobení: *
- dělení: /
Při počítání je výhodné využívat odkazy na jiné buňky. Pokud se změní hodnota v buňce, z níž se berou data pro výpočet, změní se i výsledek výpočtu.
Příklady výpočtů: vymyšlení živočichové
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | oči | nohy | umí plavat | počet v bažině | |
| 2 | mažout | 5 | 9 | ano | 15 |
| 3 | pabuch | 6 | 5 | ne | 3 |
| 4 | slizolop | 9 | 3 | ano | 7 |
=B2+B4spočítá součet očí mažouta a slizolopa=C2-C3spočítá rozdíl mezi počtem nohou mažouta a pabucha=C3*E3spočítá počet nohou všech pabuchů v bažině
V tabulkovém procesoru je mnohdy výhodné rozšířit vzorec do nových řádků, a to sice obvykle kliknutím na pravý dolní roh buňky a tažením.
Příklad: rozšíření vzorce
Pokud bychom v řádku 2 spočítali hmotnost avokád, mohli bychom jednoduše rozšířit vzorec s výpočtem do řádků, které se týkají dalších druhů zeleniny.
Tabulky: rozsahy
Rozsahy, které obsahují víc než jednu buňku, zapisujeme pomocí dvojtečky:
A2:A4zadává rozsah tvořený třemi buňkami (A2,A3aA4) v prvním sloupci.
C3:F7zadává rozsah, který se táhne přes pět řádků (3,4,5,6,7) a čtyři sloupce (C,D,E,F). Tento rozsah má5 * 4 = 20buněk.Rozsahy
A3:F3aC1:E4mají společné buňkyC3,D3aE3.
Funkce mohou brát jako některé ze svých vstupních argumentů rozsah(y).
NahoruVýraz
=SUM(B1:C2)vypočítá součet čísel v buňkáchB1,B2,C1aC2.
Tabulky: odkazy
Odkazy umožňují používat ve vzorcích hodnoty z jiných buněk. Mějme např. odkaz B3, který směřuje na hodnotu ve sloupci B na řádku 3. Vzorec =B3*2 by pak vypsal dvojnásobek hodnoty v buňce B3.
Často se hodí vzorec rozšířit do dalších buněk tabulky přetažením či pomocí schránky, abychom podobný výpočet provedli na dalších datech.
Relativní odkaz se změní, když jej rozšíříme či nakopírujeme do jiné buňky. Pokud bychom vzorec =B3*2 rozšířili směrem doprava, v nové buňce by se změnil na =D3*2.
Absolutní odkazy obsahují znak dolaru ($). Část odkazu za tímto symbolem se „uzamkne“ a při kopírování/přesouvání odkazu se nemění. Pokud bychom vzorec =$B$3*2 rozšířili směrem doprava, v nové buňce by měl zcela stejnou podobu.
V rámci absolutních odkazů je možné při přesouvání/kopírování učinit neměnným jen sloupec ($B3 se změní jen při přesunu nahoru/dolů) či jen řádek (B$3 se změní jen při přesunu doleva/doprava).
Absolutní odkazy lze používat i při vyjadřování rozsahů v argumentech funkcí, např. =SUM($A1:$E1) sečte vždy prvních pět buněk v řádku.
Tabulky: funkce
V tabulkovém procesoru lze používat funkce. Jejich využití vypadá takto: =NÁZEVFUNKCE(argument). Argument představuje data, s nimiž funkce bude pracovat. Může se jednat o číselné hodnoty (např. 2, 0,01), odkazy na buňky či rozsah (např. B2, B2:C5), vzorce či další funkce. Argumenty se v českém uživatelském prostředí oddělují středníkem (;), v anglickém čárkou (,).
Základní funkce (mimo těch souvisejících s podmínkami) uvádíme dále. Cvičení v této kapitole pracují hlavně s anglickými názvy funkcí (ty často odpovídají označení funkcí v programovacích jazycích).
| funkce | význam | název v češtině |
|---|---|---|
SUM(rozsah) |
Spočítá součet hodnot v rozsahu. Např. =SUM(A1:A3) spočítá =A1+A2+A3. |
SUMA |
MIN(rozsah) |
Najde nejmenší hodnotu v rozsahu. | |
MAX(rozsah) |
Najde největší hodnotu v rozsahu. | |
AVERAGE(rozsah) |
Spočítá aritmetický průměr hodnot v rozsahu. Aritmetický průměr čísel 1, 1, 1, 2, 55 je 12. |
PRŮMĚR |
MEDIAN(rozsah) |
Spočítá medián hodnot v rozsahu (medián je číslo, které je větší nebo rovno alespoň polovině hodnot a zároveň menší nebo rovno alespoň polovině hodnot). Medián čísel 1, 1, 1, 2, 55 je 1. |
|
COUNT(rozsah) |
Spočítá počet buněk s číselnými hodnotami v rozsahu. | POČET |
ABS(číslo) |
Spočítá absolutní hodnotu čísla. | |
SIGN(číslo) |
Spočítá znaménko čísla (-1 pro záporné, 0 pro nulu a 1 pro kladné číslo). |
|
ROUND(číslo; počet) |
Zaokrouhlí číslo na zadaný počet desetinných míst, pokud není zadaný počet, zaokrouhluje se na celá čísla. | ZAOKROUHLIT |
ROUNDUP(číslo; počet) |
Zaokrouhlí číslo nahoru na zadaný počet desetinných míst. Pokud není zadaný počet, zaokrouhluje se na celá čísla. Lze zadat záporný počet desetinných míst, např. počet -3 znamená zaokrouhlení nahoru na tisíce. |
|
ROUNDDOWN(číslo; počet) |
Zaokrouhlí číslo dolů na zadaný počet desetinných míst. Pokud není zadaný počet, zaokrouhluje se na celá čísla. Lze zadat záporný počet desetinných míst, např. počet -1 znamená zaokrouhlení dolů na desítky. |
|
DEGREES(úhel) |
Převede úhel v radiánech na úhel ve stupních. DEGREES(1,570796327) vyjde 90. |
|
RADIANS(úhel ve stupních) |
Převede úhel ve stupních na úhel v radiánech. RADIANS(90) vyjde 1,570796327. |
|
SIN(úhel) |
Spočítá sinus úhlu, úhel je zadaný v radiánech. SIN(1,570796327) vyjde 1. |
|
COS(úhel) |
Spočítá kosinus úhlu, úhel je zadaný v radiánech. COS(1,570796327) vyjde 0. |
Tabulky: podmínky
Použití podmínek v tabulkovém editoru umožňuje určité buňky ovlivnit přítomností hodnot v jiných buňkách. Dále uvádíme přehled funkcí souvisejících s podmínkami včetně příkladů navázaných na ukázkovou tabulku.
| funkce | použití | příklad (s tabulkou níže) | obvyklý název funkce v češtině |
|---|---|---|---|
IF(podmínka; když pravda; když nepravda) |
Vypíše text či použije vzorec na základě obsahu jiné buňky. | =IF(E2>10;"hodně";"málo") vypíše hodně (Diorit má více než 10 předmětů). |
KDYŽ |
COUNTIF(rozsah; podmínka) |
Spočítá výskyty hodnot v rozsahu odpovídající podmínce. | =COUNTIF(E2:E5;">10") vypíše 2 (2 pralidé mají více než 10 předmětů). |
|
SUMIF(rozsah; podmínka) |
Sečte hodnoty v rozsahu, které odpovídají podmínce. | =SUMIF(E2:E5;">10") vypíše 30 (sčítáme předměty těch pralidí, kteří jich mají více než 10). |
V rámci kritérií podmínek je možné používat logické spojky NOT (negace, česky NE), AND (A) či OR (NEBO). Např. =IF(OR(B2>3;C2>3);TRUE;FALSE) vypíše, zda má Diorit více než 3 rohy pratura či perly (TRUE).
Databáze slouží ke strukturovanému ukládání informací a mají dnes široké použití. Nejrozšířenějším typem databází jsou relační databáze, ve kterých se data ukládají v podobě tabulek.
Pro práci s databázemi se používají dotazovací jazyky (query languages). Tyto jazyky obvykle umožňují nejen databáze vytvářet a modifikovat, ale především v nich vyhledávat informace. Velmi často se používá jazyk SQL.
- Základy SQL – tvorba tabulek, vkládání a aktualizování záznamů, jednoduché vyhledávání
- Select – příkaz pro vyhledání informací v databázi
Použití databází
Databáze slouží ke strukturovanému ukládání informací. Jako uživatelé se s nimi běžně nesetkáme, existují však na pozadí mnoha webových stránek a služeb, které využíváme. Typickou databázi si můžeme představit jako několik popropojovaných tabulek s pojmenovanými sloupci, takzvanými atributy, kde řádky jsou jednotlivé záznamy.
Vlastnosti databází
Data v databázi musí být snadno vyhledatelná. Také je žádoucí, aby bylo možné nová data snadno přidávat a měnit. Protože se v databázích často ukládají i citlivá data, pro zajištění bezpečnosti uložených informací se databáze obvykle šifrují. Pro zvýšení bezpečnosti je často možné vynutit vlastnosti dat vkládaných do databáze; například jednotlivým sloupcům bývají přiřazeny datové typy, tedy informace, zda se jedná například o číslo nebo řetězec omezené délky.
Práce s databázemi
Pro vytváření a práci s databází se v praxi obvykle používá databázový software, například MySQL nebo Microsoft Access, se kterým se pracuje pomocí speciálního dotazovacího jazyka SQL.
Často je potřeba provést více než jednu operaci na databázi, například odečíst peníze z jednoho účtu a přičíst je na jiný. Případu, kdy je nezbytné, aby se buďto provedly všechny změny anebo žádná, říkáme transakce.
NahoruRelační databáze
Aby se v databázích dalo snadno vyhledávat a rozšiřovat je, používají se různé databázové architektury, které nám toto umožní.
Nejrozšířenějším typem jsou relační databáze. Data se zde ukládají v tabulkách. Jednotlivé záznamy jsou uloženy v řádcích tabulky a každý záznam odpovídá jedné entitě (například konkrétní osobě, věci apod.). Sloupce tabulky odpovídají atributům, tedy jednotlivým vlastnostem záznamů. V hlavičce tabulky najdeme názvy jednotlivých atributů a někdy i jejich datové typy, tedy omezení na hodnoty, které je možné do daného pole ukládat. Příkladem datového typu je int, který značí celé číslo, nebo char[20], který značí textový řetězec z maximálně 20 znaků.
Vyhledávání v tabulce nám zjednodušují kandidátní klíče — skupiny atributů, které jednoznačně identifikují a odliší každý záznam v tabulce. Z kandidátních klíčů se pro každou tabulku vybírá jeden primární klíč. Jedna relační databáze se obvykle skládá z většího množství tabulek, které mezi sebou můžeme propojovat pomocí primárních klíčů a vyhledávat tak odpovědi na složitější dotazy o našich datech. Primární klíč jedné tabulky použítý v jiné tabulce se v jejím kontextu nazývá cizí klíč.
Existují i další hojně používané typy databází. V posledních letech se rozšiřují možnosti ukládat nestrukturovaná data, například NoSQL databáze.
NahoruSQL: základy
Příklady použití příkazů jazyka SQL
CREATE TABLE fish(name varchar(80), age int)Vytvoří tabulku s názvem fish a atributy name typu varchar(80) a age typu int.
DROP TABLE fishOdstraní celou tabulku fish.
INSERT INTO fish VALUES ('Julie', 1, 'neonka červená')Přidá do tabulky fish nový záznam o rybě Julii.
DELETE FROM fish WHERE name = 'Alice'Odstraní záznam o rybě jménem Alice. Pomocí WHERE můžeme definovat různé podmínky výběru záznamů.
UPDATE fish SET age = 0Nastaví věk všech ryb na 0. Přidáním WHERE můžeme omezit záznamy, které upravíme.
SELECT name FROM fish WHERE age = 7Zobrazí jména všech ryb, kterým je 7 let.
Všechny příkazy kromě SELECT nějakým způsobem modifikují tabulky, SELECT obsah databáze nijak nemění a pouze vrací informace v podobě tabulky. SQL příkazy se dají nejen řetězit, ale i kombinovat do sebe; například je možné volat SQL příkaz na tabulce vrácené příkazem SELECT.
Entitně-vztahové modely
Entitně-vztahové modely (diagramy) pomáhají znázorňovat a zpřehledňovat vztahy a vlastnosti mezi objekty. Používají je například databázoví architekti, aby naplánovali, jak bude vypadat jejich databáze. Diagramy jsou ale poměrně jednoduché, takže si s nimi můžeme pohrát i my.
V entitně-vztahovém modelu se vyskytují tři typy prvků:
- Entity představují objekty. Mohou existovat samostatně, nezávisle na ostatních objektech, a mají vlastnosti (atributy). V diagramu se zakreslují do obdélníků.
- Vztahy (relace) propojují entity. Zakreslují se jako diamanty, které jsou spojené čarou s danými entitami.
- Atributy (vlastnosti) patří jednotlivým entitám. Typicky nemají smysl bez entity, které patří – nemohou existovat samostatně. Znázorňují se jako elipsy spojené s danou entitou.
Jednoduchý diagram může vypadat například takto:
Rozebraný příklad: význam diagramu
- Uživatelé sociální sítě mohou zveřejňovat příspěvky a mají určitý počet sledujících.
- Uživatelé a příspěvky jsou entity.
- Jsou propojené vztahem, jehož název říká, jak spolu tyto dvě entity souvisí (uživatel zveřejňuje příspěvek).
- Počet sledujících je atribut uživatele.
Vztahy mohou mít různé četnosti. Četnosti vyjadřují, s kolika entitami může být každá strana v daném vztahu. Uvažme zmíněný příklad sociální sítě. Jeden uživatel může zveřejnit více příspěvků. Ale každý příspěvek je zveřejněn pouze jedním uživatelem. Proto je četnost vztahu „zveřejňuje“ 1 uživatel – více příspěvků. Naproti tomu, pokud bychom mluvili o vztahu „uživateli se líbí příspěvek“, byla by četnost více uživatelů – více příspěvků. To proto, že jednomu uživateli se může líbit více příspěvků, a jeden příspěvek může být „olajkován“ více uživateli.
Kromě entitně-vztahových modelů můžeme vztahy mezi objekty znázorňovat například i pomocí grafů. Pro znázornění postupného běhu programu se naopak používají vývojové diagramy.
NahoruRegulární výrazy
Kdykoliv potřebujete v textu něco nahradit, najít nebo poupravit, můžete k tomu využít regulárních výrazů. Především u rozsáhlejších textů je jejich používání velice užitečné. Regulární výrazy mají široké uplatnění v mnoha programovacích jazycích (především skriptovacích jako Python, PHP, Perl, JavaScript). Můžete je ale použít i unixových příkazech (např. grep) nebo v textových editorech (např. Notepad++, Emacs). Regulární výrazy jsou velice bohaté. V našich příkladech shrneme především základní operátory.
NahoruZákladní vyhledávání
Základními prvky regulárních jazyků jsou obyčejná písmena. Ty při vyhledávání odpovídají přímo sobě. Pokud tedy zadáme regulární výraz kr, tak mu budou odpovídat slova, která obsahují podřetězec „kr“.
Tečka odpovídá libovolnému znaku.
Metaznaky jsou speciální znaky, které používáme na konstrukci regulárních výrazů (např. .*+?). Co když ale chceme hledat právě tyto znaky? Na to použijeme zpětné lomítko, které ruší význam metaznaku a chápe jej jako znak obyčejný.
Skupiny znaků
Pomocí následujících speciálních znaků můžeme v regulárním výrazu označit skupiny písmen:
[] |
výběr znaku v závorkách, např. [aeiouy] značí libovolnou z uvedených samohlásek |
[ - ] |
výběr znaku z intervalu, např. [a-z] značí libovolné malé písmeno anglické abecedy |
[^ ] |
negovaný výběr znaku, např. [^aeiouy] značí vše kromě uvedených samohlásek |
\d |
číslice (to samé jako [0-9]) |
\D |
vše kromě číslic (to samé jako [^0-9]) |
\w |
alfanumerické znaky (to samé jako [a-zA-Z0-9_]) |
\W |
vše kromě alfanumerických znaků (to samé jako [^a-zA-Z0-9_]) |
\s |
„bílé” znaky (mezera, tabulátor, znaky pro zalomení řádků) |
\S |
vše kromě „bílých” znaků |
Dále můžeme využít následující konstrukce, které vymezují více možností, případně seskupují znaky k sobě:
| |
odděluje několik dílčích výrazů (ahoj|nazdar odpovídá právě jednomu z pozdravů) |
() |
podřetězec, na nějž je možno aplikovat kvantifikátor (ko(ko)?s odpovídá právě kos a kokos) |
Kvantifikátory
Kvantifikátory v regulárních výrazech vyznačují, kolikrát se má předcházející výraz opakovat. Například hvězdička v pe*s značí libovolný počet výskytů písmene e.
* |
libovolný počet opakování |
+ |
jedno nebo více opakování |
? |
volitelný výskyt (~ 0 nebo 1 opakování) |
{n} |
právě n výskytů |
{n,m} |
nejméně n, nejvíce m výskytů |
Pomocí následujících speciálních znaků můžeme v regulárním výrazu označit hranice (začátek, konec) slov i celých řetězců:
^ |
začátek řetězce |
$ |
konec řetězce |
\b |
začátek či konec slova |






