Výpis souhrnů
Algoritmické myšlení
Podtémata
- Algoritmické myšlení
- Rozpoznávání vzorů
- Stejné vzory
- Společná vlastnost
- Vzory v posloupnostech
- Popis vzorů
- Rozklad obrázků na části
- Posloupnosti příkazů
- Základní akce
- Pořadí příkazů
- Souběžné akce
- Vstup a výstup
- Vnořené bloky
- Cykly a podmínky
- Opakuj N×
- Události
- Podmínky a větvení
- Opakuj dokud
- Opakované rozhodování
- Vnořené cykly
- Proměnné
- Proměnné: základní princip
- Proměnné: obecné principy
- Výrazy s proměnnými
- Cykly s proměnnými
- Podmínky s proměnnými
- Typy proměnných
- Pojmenování proměnných
- Použití proměnných
- Funkce a zobecňování
- Abstrakce
- Funkce bez parametrů
- Funkce s parametry
- Zobecňování programů
- Rozklad programů
- Rekurze
- Ladění, hledání chyb
- Úprava programů
- Vývojové diagramy
Algoritmické myšlení
Algoritmické myšlení je součást obecnějšího informatického myšlení, která se zaměřuje na navrhování algoritmů.
Co zahrnuje algoritmické myšlení?

Algoritmus je přesně daný postup, kterým řešíme určitý problém. Algoritmické myšlení se typicky využívá při programování, tj. při zápisu algoritmů, které provádí počítač. Má však svoje využití i v běžném životě: typickými příklady jednoduchých algoritmů jsou recepty na vaření nebo instrukce k sledování cesty z jednoho místa na druhé.
Algoritmické myšlení zahrnuje nejen tvorbu algoritmu, ale i další související kroky:
- Porozumění problému, jasná formulace problému.
- Abstrakce, rozklad problému na podčásti, odlišení podstatných prvků od těch, které jsou méně důležité.
- Zvážení různých přístupů k řešení problému, porovnání efektivity algoritmů, optimalizace postupů.
- Porozumění algoritmu, který vymyslel někdo jiný, a jeho provedení.
- Hledání a opravování chyb.
Algoritmické myšlení v
Téma dělíme na několik podtémat:
- Rozpoznávání vzorů – vyhledávání společných vzorů a vlastností, vzory v posloupnostech, popis vzorů
- Posloupnosti příkazů – skládání algoritmů z více příkazů
- Cykly a podmínky – opakované a podmíněné vykonávání příkazů
- Proměnné – práce se stavovou informací, ukládání hodnot do proměnných
- Funkce a zobecňování – zobecňování (abstrakce) vzorů, rozklad (dekompozice) problémů na části, použití funkcí
- Vývoj programů – ladění, hledání chyb
Příklady v této části staví především na „mikrosvětech“, což jsou jednoduchá, intuitivní prostředí s omezeným množstvím příkazů a současně zajímavou dynamikou. Jsou začleněny jak variace na často používané principy (želví grafika, robot na mřížce), tak originální variace jako kouzla nebo deaktivace bomby.
Pro zápis programů zde využíváme blokové programování, k jehož použití nabízíme samostatný metodický text pro učitele.
NahoruRozpoznávání vzorů
Abychom byli schopni řešit problémy, pracovat s daty a vymýšlet algoritmy, musíme být schopni hledat pravidelnosti a vzory. Nalezené vzory se následně snažíme využít pro hledání společných prvků a zobecňování, která nám umožní tvořit efektivní řešení.
Rozpoznávání vzorů je důležitá dovednost pro řešení problémů i práci s daty. Pomáhá nám všímat si pravidelností, podobností a rozdílů, díky nimž můžeme lépe porozumět světu kolem sebe a vytvářet efektivní řešení. V informatice i v každodenním životě se s rozpoznáváním vzorů setkáváme velmi často — od třídění informací po tvorbu algoritmů.
Příklad ze života: Karel a jeho nákupy
Ilustrativní, zjednodušený příklad ze života:
- Karlovi neustále dochází peníze, tak si začal zapisovat výdaje.
- Nejdříve si do sešitku zapisuje výdaje zcela konkrétně, např. „kniha Hobit, 243 Kč“, „chleba a sýr na večeři, 58 Kč“. Z takového zápisu je ale těžké se poučit.
- Karel prohlédne výdaje, najde pravidelně se vyskytující typy výdajů a použije zobecňování: výdaje rozdělí do vhodných kategorií („jídlo“, „oblečení“, „studium“, …).
- Následně si výdaje přepíše do tabulkového editoru. Ten mu umožní snadno vypočítat celkové výdaje v jednotlivých kategoriích.
- Karel tak zjistí, že utrácí až příliš za oblečení. Ví, na čem je, a může s tím něco dělat.
- Stejné vzory – Hledáme stejné dvojice v jednoduchých i složitějších případech (typicky obrázková zadání).
- Společná vlastnost – Určujeme, co mají vybrané prvky společného (např. společný prvek obrázků, společná vlastnost slov).
- Vzory v posloupnostech – Odhalujeme pravidla a doplňujeme chybějící prvky (čísla, symboly).
- Popis vzorů – Vyjadřujeme nalezené pravidelnosti slovy nebo jednoduchými diagramy.
- Odhalování skrytých pravidel – Pozorujeme několik příkladů a snažíme se odhalit tajné pravidlo.
- Rozklad obrázků na části – Zjišťujeme, z jakých prvků se složitější obrázek skládá.
Výukové moduly
Inspiraci pro začlenění tohoto tématu do výuky nabízí výukové moduly, které poskytují konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí.
| 2.–4. ročník | |
| 4.–5. ročník |
Stejné vzory
Než se vrhneme na hledání složitějších vzorů, hodí se umět rozpoznat vzory, které jsou úplně stejné. Ani to totiž nemusí být úplně jednoduché. Někdy je potřeba se dobře soustředit na detaily. Jindy mohou být vzory sice stejné, ale trochu jinak otočené a na rozpoznání těch stejných musíme zapojit prostorovou představivost.
NahoruSpolečná vlastnost
Abychom mohli hledat vzory a vytvářet algoritmy, musíme si umět všímat společných vlastností mezi věcmi, které třeba na první pohled vypadají rozmanitě. Hledání společných vlastností je speciální případ Abstrakce, kterou při algoritmizaci často využíváme. Tuto dovednost využijeme například u Rozkladu obrázku na části.
Příklady:
- pes, ves, hrb, kos – společný počet písmen (3)
- kos, sova, vrabec, datel – společné téma (ptáci)
- brečí, výpravčí, lehčí, Meziříčí – společná písmena (slova končí na -čí)
Vzory v posloupnostech
Hledání pravidelností a vzorů v posloupnostech je užitečný trénink základního rozpoznávání vzorů. Pro základní trénink většinou používáme posloupnosti čísel či obrázků s přesně daným pravidelným chováním. Příklady tohoto typu se někdy používají i pro testování inteligence.
Ve složitějších variantách má hledání vzorů v posloupnostech v informatice mnoho aplikací: pomocí nalezených vzorů můžeme například předpovídat budoucí chování, odhalovat chyby v datech nebo provádět kompresi dat.
Kromě níže uvedených interaktivních cvičení je k dispozici také Pracovní list: doplňování vzorů (+ řešení), který obsahuje zadání typu „Ravenovy progresivní matice“, které se často používají v IQ testech (v mřížce 3 × 3 jsou umístěny různé geometrické obrazce, cílem je doplnit chybějící).
NahoruPopis vzorů
Pomocí programů můžeme zapisovat složité algoritmy a popisovat komplikované vzory. Ale pro zápis jednoduchých vzorů nepotřebujeme programovací jazyky, vystačíme klidně i se zápisem pomocí šipek. Ani to nemusí být úplně jednoduché. Třeba taková záměna pořadí šipek může vést k úplně jinému vzoru.
NahoruRozklad obrázků na části
Velmi užitečný přístup k řešení problémů je rozložit problém na dílčí části, které jsou pokud možno co nejvíce nezávislé, a následně řešit tyto části jednu po druhé.
Příklad z běžného života: Potřebujeme se nachystat na putovní výlet na hory. Je potřeba zařídit spoustu věcí a můžeme se cítit přehlceni a snadno na něco důležitého zapomenout. Může pomoct, když si celkový problém příprava na hory rozdělíme na dílčí podproblémy: 1) naplánovat trasu a najít spoj, 2) vymyslet jídelníček a nakoupit jídlo, 3) nachystat tábornické vybavení a zkontrolovat jeho stav, 4) rozmyslet a nabalit oblečení. Tyto dílčí úkoly jsou do velké míry na sobě nezávislé a mohou je tudíž řešit různí lidé. I pokud je řeší ten stejný člověk, tak se při řešení dílčího podproblému může soustředit pouze na něj, což mu postup usnadní.
Příklad z programování: Programy nepíšeme jako dlouhé seznamy příkazů, ale dělíme je na funkce, z nichž každá řeší nějaký dílčí problém. Rozdělení na podproblémy je klíčovým prvkem dobrého návrhu programů.
Rozklad problémů na části je složitá dovednost, kterou se člověk učí dlouhodobou praxí. Pro základní trénink nabízíme příklady s obrázky. Složitě vypadající obrázek často lze vytvořit z jednoduchých částí, které pouze vhodným způsobem poskládáme.
NahoruPosloupnosti příkazů
Algoritmy jsou tvořeny posloupnostmi příkazů, které určují, co má počítač vykonat (vypiš znak A, nakresli jablko, popojdi dopředu). Při programování je proto potřeba vědět, které příkazy máme k dispozici a jaký je jejich přesný význam. Jednotlivé příkazy pak skládáme do posloupností, a tím vytváříme složitější programy. Důležité je pořadí příkazů, protože různá pořadí mohou vést k výrazně odlišnému chování (pokud se otočíme doprava a uděláme krok vpřed, dojdeme jinam, než když nejprve uděláme krok vpřed a teprve potom se otočíme).
- Základní akce – jednoduché příklady na pochopení významu základních akcí, ze kterých pak následně budeme skládat složitější programy
- Pořadí příkazů – rozlišování mezi různými pořadími příkazů, přiřazování výsledků k posloupnostem příkazů
- Souběžné akce – příklady, kde se příkazy vykonávají zároveň
- Změna stavu – situace, kde se při vykonávání programu mění stav prostředí a to pak ovlivňuje chování programu
- Vstup a výstup – programy, které získávají údaje z okolí a své výstupy zase nějak zobrazují či zapisují
- Vnořené bloky – krok k tvorbě složitějších programů pomocí seskupování do bloků, které se pak vykonávají společně
Tipy k procvičování
Algoritmické myšlení se nejlépe procvičuje prakticky tvorbou programů. Zkušení programátoři píší programy v textových programovacích jazycích jako je například Python. Pro začátečníky je ale lepší začít s grafickým programováním pomocí bloků, protože u toho se nemusí řešit detaily zápisu, ale mohou se soustředit na samotné algoritmy.
- Jako rozcvička a cvičení pro úplné začátečníky je vhodná Šipkovaná.
- Typický způsob procvičování základů algoritmického myšlení spočívá v interaktivním řešení úloh formou blokového programování. To nabízí cvičení Želví grafika, ProgMalování, Stavitel.
- Další cvičení (Rozhodovačka, Pexeso, Přesouvání, Krok po kroku) nabízí cílenější procvičení dílčích dovedností. Tato cvičení nemusí být tak atraktivní jako tvorba vlastních programů, ale jsou velmi užitečná pro důkladné pochopení principů.
Konkrétní náměty na postup procvičování nabízí následující výukový modul:
Základní akce
Programy se skládají z jednotlivých příkazů. V našich úlohách na procvičování můžete například potkat:
- příkazy pro vypsání textu nebo nakreslení jednoduchého obrázku:
vypiš,nakresli, - příkazy pro pohyb (
dopředu,zatočit doprava), - provedení kouzla (
vyčaruj klobouk,změň na žábu).
Při praktickém programování používáme například příkazy pro vypsání textu na monitor, vykreslení obrázku, načtení informace ze souboru nebo uložení výsledku výpočtu do paměti počítače.
Z dílčích příkazů následně skládáme programy pomocí posloupností příkazů, opakování, podmínek a dalších metod.
NahoruPořadí příkazů
Základním krokem jakéhokoliv algoritmu je provádění posloupnosti akcí v předepsaném pořadí. Pořadí, v jakém akce provádíme, je důležité. Někdy je to úplně jasné. Když připravujeme palačinky, musíme nejdříve těsto zamíchat, a až potom dát na pánvičku. Kdybychom pořadí akcí prohodili, nedopadlo by to příliš palačinkově. Podobně to dopadne, když chystáme program pro robota. Pokud se robot nejdřív otočí a pak udělá krok, dopadne to jinak, než když udělá krok a pak se otočí.
Význam pořadí akcí je dobře vidět třeba ve cvičení ProgMalování, kde je velmi důležité, který obrázek nakreslíme dříve a který později:
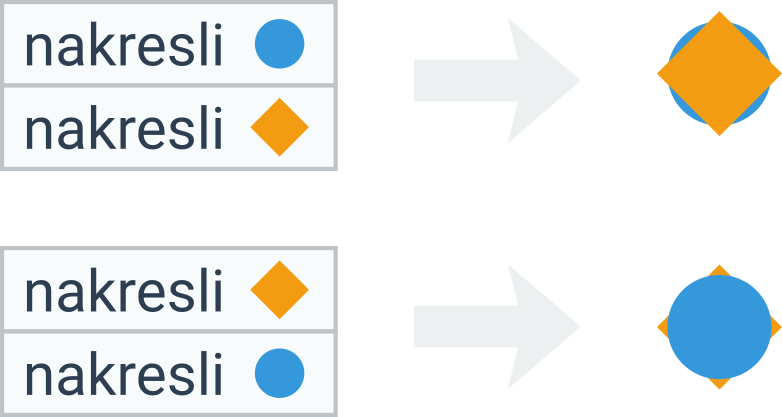
Pořadí příkazů zapisujeme v programech stejně jako při psaní běžného textu: odshora dolů (případně zleva doprava).
NahoruSouběžné akce
V pokročilé informatice se rozlišuje souběžnost a paralelismus, zde však do těchto detailů nebudeme zacházet. Tyto pojmy označují souběh více dějů současně. To je pochopitelně něco, co se ve světě kolem nás děje neustále. Pokud se však snažíme vymýšlet algoritmická řešení problémů, je souběžnost většinou oříšek. Není totiž vůbec jednoduché souběh více událostí správně naplánovat.
Pro trénink přemýšlení o souběžnosti využijeme především úlohy na čtverečkované mřížce, kde se současně pohybuje několik agentů.
NahoruVstup a výstup
Příkazy vstupu a výstupu umožňují programům interagovat se světem. Základní průběh výpočtu obsahuje posloupnost vstup → zpracování → výstup. Programy ale mohou obsahovat více příkazů vstupu i výstupu. Ve hře se po každém stisknutí šipky (vstup) vykreslí nová poloha ovládané postavy (výstup).
Příkazy vstupu
Příkazy vstupu získávají data ke zpracování. Vstup lze načítat buď od uživatele skrze různá vstupní zařízení (např. myš, klávesnice, dotykový displej), ze souboru uloženého v počítači (např. uložený stav hry), nebo ze senzorů vnímajících okolní prostředí (např. vzdálenost robota od překážky, zjištění barvy políčka, detekce hrany v Plošinovce).
Příkazy pro načítání vstupu typicky čekají na načtení dat (např. dokud uživatel nezadá odpověď), teprve potom program pokračuje dalším příkazem. Alternativou je definovat kód, který se spustí při určité vstupní události (např. kliknutí myši), toho se často využívá v hrách (i v Plošinovce) a jiných grafických aplikacích.
Příkazy výstupu
Příkazy výstupu předávají výsledek zpracování. Výstup lze předat uživateli skrze různá výstupní zařízení (monitor, reproduktor), nebo uložit do souboru pro pozdější využití (např. uložení aktuálního stavu hry). Výstup může mít různou formu, například text (výpis na obrazovku), grafika (vykreslení herní scény), zvuk (varovné pípnutí), nebo akce stroje vykonávajícího program (např. pohyb robota).
Programy se vstupem a výstupem
Ne všechny příkazy jsou vstupní či výstupní. Například následující program má 2 příkazy vstupu (načti), 4 příkazy výstupu (vypiš) a 1 příkaz pro zpracování načtených dat (nastav), který není ani vstupní, ani výstupní.

Některé programy nemusí mít žádný vstup – dělají pokaždé to samé. (Například programy v želví grafice kreslí vždy jeden konkrétní obrázek.) Všechny užitečné programy však mají nějaký výstup.
NahoruVnořené bloky
Kromě jednoduchých příkazů (vypiš, jdi dopředu, zatoč) existují příkazy složené (opakuj, pokud), které umožňují kombinovat více příkazů dohromady a přehledně strukturovat kód do bloků. (V blokovém programování máme „blok“ pro každý příkaz, v textových programovacích jazycích se pojem „blok“ používá pouze pro složené příkazy.)

Využití složených příkazů
Složené příkazy se používají hlavně k řízení průběhu výpočtu (např. opakování příkazů, podmíněné příkazy. Lze je také využít na nastavení dočasného kontextu (např. soubor pro zápis dat, barva písma).

Struktura bloků
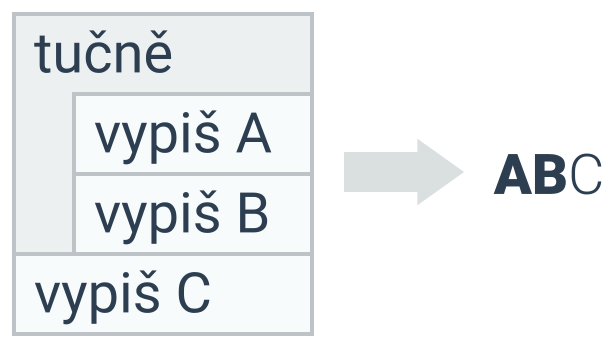
Složené příkazy mají většinou hlavičku a tělo. Tělo je libovolná posloupnost příkazů (např. vypiš A). Hlavička pak specifikuje, jak se tyto příkazy budou vykonávat (např. opakuj 3×). Bloky lze do sebe vnořovat – uvnitř bloku (složeného příkazu) může být další blok (složený příkaz) . V následujícím programu nastavuje vnější blok tučné písmo, vnořený (vnitřní) blok nastavuje žluté písmo. Písmena B a C jsou žluté i tučné.

Vymezení bloků
Důležité je správné určení, které příkazy jsou součástí těla bloku a které jsou už mimo něj. Různé programovací jazyky využívají různé přístupy k vymezení začátku a konce těla bloku, dva nejčastější způsoby jsou odsazení pomocí mezer a složené závorky. V následujícím programu jsou výpis A a B součástí bloku s tučným písmem (jsou odsazené), výpis C už je mimo něj (není odsazený).
Cykly a podmínky
Jakmile máme zvládnuté základní posloupnosti příkazů, můžeme budovat složitější programy za využití cyklů a podmínek:
Opakuj N× – základní cyklus se zadaným počtem opakování
opakuj 4×: krok dopředu, zatoč doprava
Události – příkazy reagující na to, když se v prostředí něco stane
při stisku klávesy: vykresli tečku
Podmínky a větvení – vykonání části programu, pouze pokud platí určitá podmínka
pokud stojíš na písku: otoč se doprava
Opakuj dokud – cyklus, který se vykonává tak dlouho, dokud je splněna podmínka
dokud je před tebou volné pole: krok dopředu
Cykly a podmínky lze kombinovat. Na to nepotřebujeme žádné speciální příkazy, ale není úplně jednoduché se naučit takové programy tvořit. Proto na to máme speciálně připravená procvičování:
- Opakované rozhodování – cyklus kombinovaný s podmínkou
- Vnořené cykly – cyklus uvnitř cyklu
Tipy k procvičování
- Před procvičováním cyklů a podmínek je vhodné důkladně procvičit posloupnosti příkazů. Zejména je potřeba vědět, v jakém pořadí jsou příkazy vykonávány.
- Určování, které příkazy patří do těla cyklu a podmínek, lze procvičit samostatně v rámci tématu vnořené bloky.
- Před vytvářením vlastních programů je užitečné procvičit čtení kódu a pochopení principu cyklů a podmínek, k tomu lze využít cvičení Kód kostky, Rozhodovačku, Pexeso, Přesouvání a Krok po kroku.
- Důkladné procvičení podmínek a cyklů pak umožňuje řešení interaktivních programovacích úloh formou blokového programování. V Želví grafice a ProgMalování lze procvičovat cykly s daným počtem opakování (i vnořené), v Plošinovce podmínky, Stavitel pak umožňuje procvičení všech cyklů i podmíněných příkazů.
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 5.–6. ročník | Úplné základy blokového programování. | |
| 5.–7. ročník | Navazující modul s podmínkami a mírně složitějšími programy. |
Opakuj N×
Kdybychom všechny algoritmy vyjadřovali jako prostou posloupnost akcí, byly by často velmi dlouhé a nepřehledné. Proto se snažíme v problémech hledat pravidelnosti a vzory a ty následně vyjádřit v algoritmu pomocí opakovaného provádění stejných instrukcí.
Základní forma opakování je cyklus s pevně daným počtem opakování (v programovacích jazycích se běžně označuje jako for cyklus). Takto například dáme želvě pokyn, aby vykreslila čtverec (který se skládá ze 4 stejných stran):

Při zápisu opakování musíme dávat dobrý pozor na to, co je součástí cyklu a co je mimo něj. Příklad:
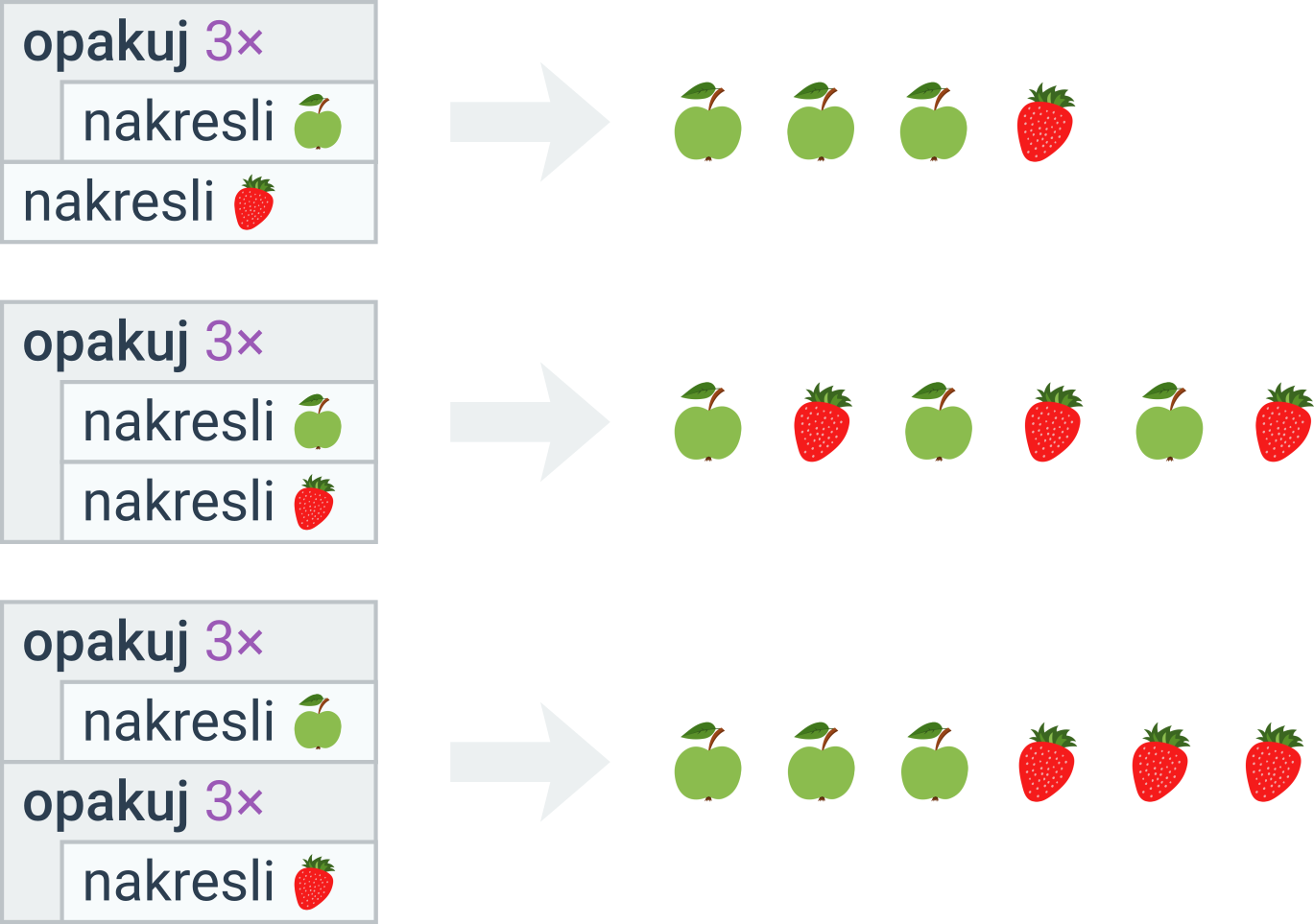
První příklad opakuje pouze vykreslování jablek, kreslení jahody je mimo cyklus. Ve druhém příkladě se opakuje vykreslování jablek i jahod. Ve třetím příkladě nejdříve nakreslíme tři jablka, potom tři jahody.
Můžeme též použít cyklus, který se opakuje tak dlouho, dokud není splněná zadaná podmínka. Tyto cykly pokrývá navazující téma opakuj dokud.
NahoruPři programování můžeme chtít, aby se nějaké akce provedly tehdy, když dojde k určité události. V Plošinovce můžeme potřebovat vyskočit při kliknutí a otočit se, když narazíme na kaktus. Hlavička bloku určuje událost, na kterou čekáme (kliknutí myši, stisknutí klávesy, doručení zprávy). Tělo bloku pak obsahuje příkazy, které se mají při dané události provést.
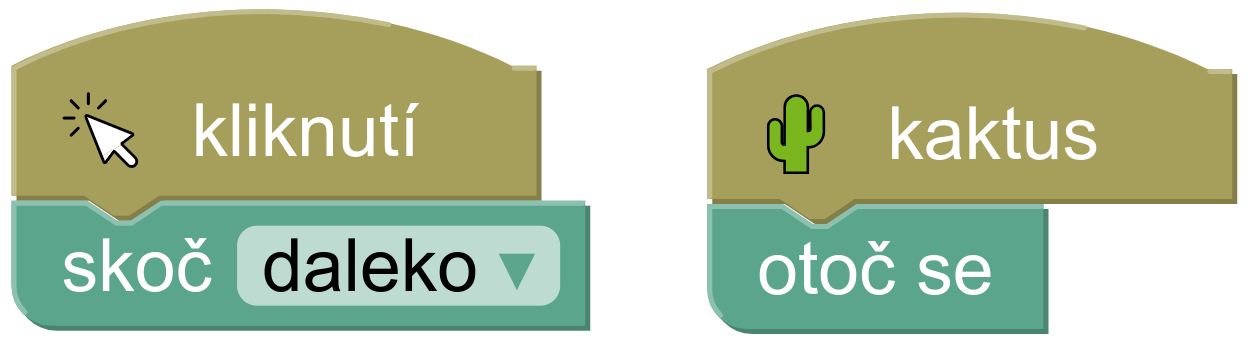
Programy s událostmi
Akce se provede vždy, když dojde k dané události. Pokud tedy k události dochází opakovaně, akce se provede vícekrát. Naopak, pokud k události nikdy nedojde, akce se neprovede ani jednou. Jeden program může obsahovat více událostí. V takovém případě se může stát, že dojde k více událostem současně a provede se několik akcí v jednu chvíli. (Události proto souvisí se souběžností.) Vytváření programů s událostmi se označuje jako událostmi řízené programování.
Události vs. podmínky
Události mohou připomínat podmíněné příkazy – v obou případech se nějaké příkazy provádí jen tehdy, když něco platí. Podmínka podmíněného příkazu se však kontroluje pouze v ten moment, když na ni při vykonávání programu narazíme, zatímco na událost se čeká během celého programu. Události jsou spouštěny konkrétními signály (např. kliknutí), zatímco podmínky mohou být obecné výrazy obsahující např. porovnávání a logické spojky. Události a podmínky lze kombinovat – tělo události může tvořit podmíněný příkaz.
Využití událostí
Události umožňují vytvářet interaktivní programy, které reagují na akce uživatele. To se běžně používá ve hrách (při stisknutí mezerníku postavička vyskočí), v aplikacích s grafickým uživatelským rozhraním (textový procesor reaguje na zmáčknutou klávesu zobrazením příslušného znaku) a ve webových aplikacích (při stisknutí na tlačítko „Odeslat“ se odešle zpráva). Lze však reagovat i na události uvnitř programu (když postavička vejde do dveří, změní se scéna).
Události ve Scratchi
Událostmi řízené programování využívá i Scratch. Kromě akcí uživatele může být událostí i obdržení zprávy, kterou rozešleme v jiné části programu.
Podmínky a větvení
U většiny algoritmů potřebujeme, aby postup závisel na aktuálním stavu. Polévku musíme zahřívat a míchat, dokud nezačne vřít. Pokud při příjezdu na křižovatku svítí červená, auto musí zastavit.
Rozhodování podle podmínek zapisujeme pomocí slov pokud a jinak (v angličtině if a else). Názorné příklady:

Někdy větev „jinak“ nepoužíváme. Pokud podmínka není splněna, tak se v takovém případě neprovede žádná speciální akce:

Při vyjadřování podmínek často využíváme logické spojky (a zároveň, nebo, negace).
NahoruOpakuj dokud
Kromě základních cyklů s pevně daným počtem opakování využíváme často v algoritmech i cyklus typu opakuj dokud. Tento cyklus se opakuje tak dlouho, dokud je splněna zadaná podmínka. V programovacích jazycích se pro zápis tohoto typu cyklu využívá příkaz while.

Pozor na rozdíl oproti podobně znějícímu podmíněnému příkazu pokud. Tělo příkazu pokud se provede nejvýše jednou, zatímco tělo příkazu dokud se může provádět opakovaně.
Všimněte si, že po provedení cyklu podmínka neplatí (vláček není na žlutém políčku). Podmínka se vyhodnocuje ještě před prvním vykonáním těla cyklu. Pokud není splněna, tak se tělo cyklu neprovede ani jednou:

Jako u všech řídicích bloků musíme dávat dobrý pozor na to, co je součástí cyklu a co je mimo něj:


Podmínka se kontroluje vždy před provedením celého bloku, nikoliv po každém příkazu:

Při vyjadřování podmínek často využíváme logické spojky (a zároveň, nebo, negace):

Opakované rozhodování
K rozhodování podle podmínky používáme podmíněný příkaz pokud. Pokud se potřebujeme rozhodovat opakovaně, můžeme podmíněný příkaz provádět opakovaně uvnitř cyklu. K opakování využíváme příkaz opakuj N× nebo opakuj dokud, případně rekurzi – vzájemně se volající funkce (ve cvičení Robotanik). Příklady:

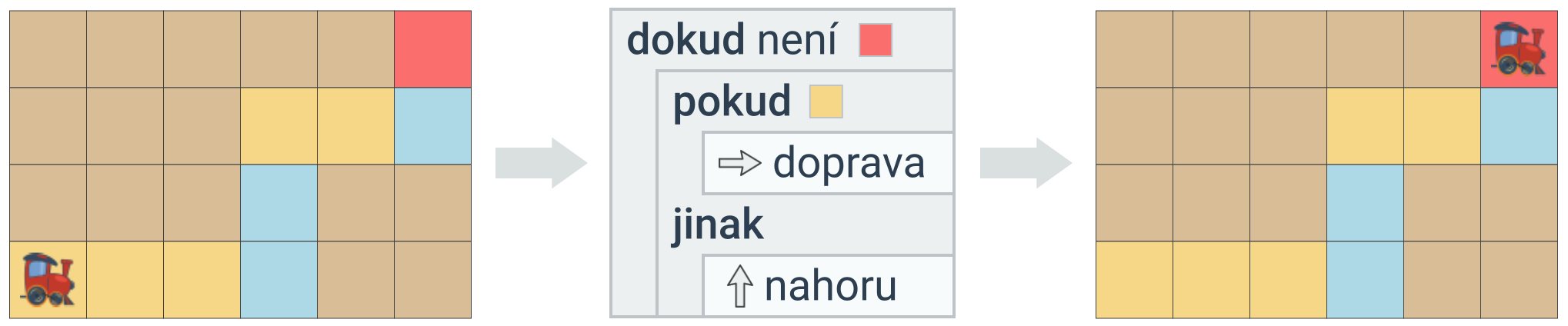
V těle cyklu může být příkazů více. Pozornost je potřeba věnovat odsazení, které určuje, který příkaz je součástí cyklu a podmíněného příkazu. V následujícím programu je příkaz nahoru součástí vnořeného podmíněného příkazu (provede se 3×), příkaz doprava je součástí cyklu, ale nikoliv podmíněného příkazu (provede se 5×) a příkaz doleva je vně cyklu (provede se pouze jednou, po skončení cyklu).

Vnořené cykly
K opakování příkazů slouží příkazy opakuj N× a opakuj dokud.
V těle cyklu mohou být nejen základní příkazy, ale třeba i další cyklus – ten nazýváme vnořený cyklus. Pro jeho použití nepotřebujeme žádný nový příkaz. Prostě jen cyklus zapíšeme (a odsadíme) uvnitř jiného cyklu:
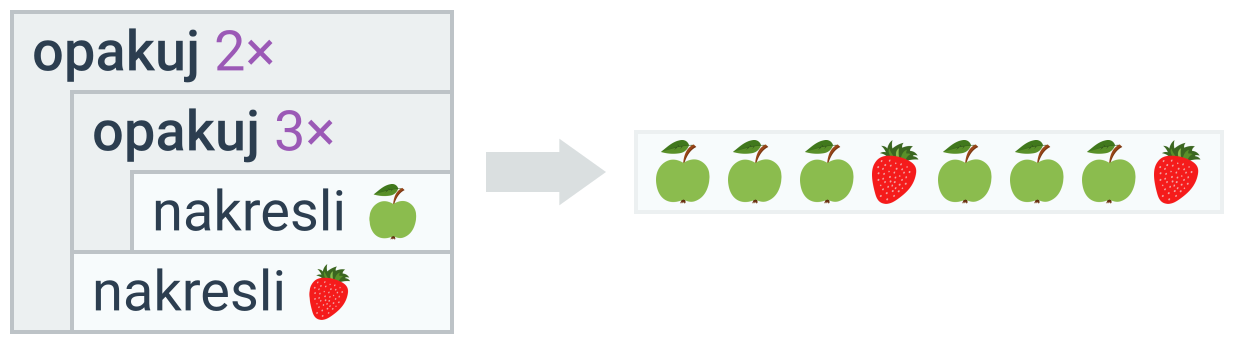
Odsazení příkazů je důležité – určuje, co je součástí kterého cyklu. Kdyby bylo kreslení jahody odsazené více, bylo by součástí vnitřního cyklu: 
Naopak, kdyby bylo kreslení jahody odsazené méně, nebylo by součástí žádného cyklu a provedlo by se až po dokončení vnějšího cyklu: 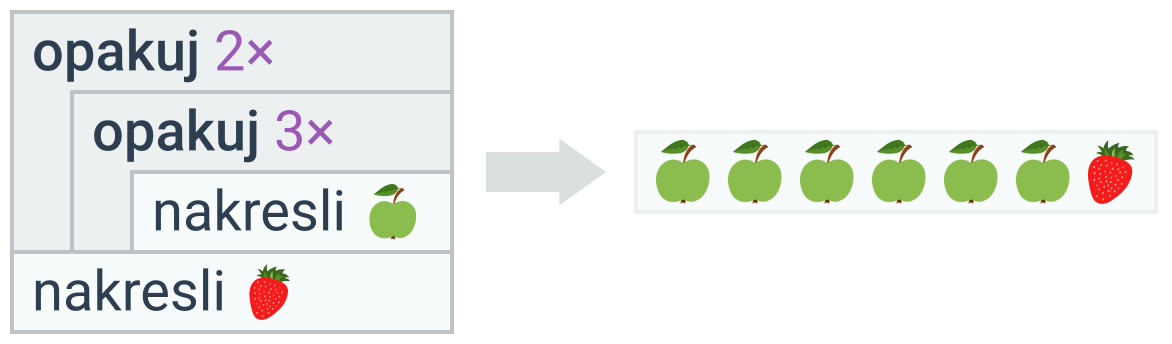
V programování je proměnná úložiště, které udržuje hodnotu. Tato hodnota se může v průběhu výpočtu měnit, od toho se také proměnná jmenuje proměnná.
Typickým příkladem použití proměnné je výpočet celkové ceny nákupu. Program v pokladně na začátku uloží do proměnné sum hodnotu 0. Při načtení každé položky nákupu, přičte její cenu do této proměnné.
Jiný příklad: V programu pro hraní piškvorek potřebujeme zjistit, jestli již jeden z hráčů vyhrál. Procházíme tedy jednotlivé směry na hracím plánu a v každém z nich počítáme, kolik křížků (či koleček) se vyskytuje v řadě za sebou. Tento počet si ukládáme v proměnné. Krom toho si do nějaké proměnné potřebujeme uložit i celý herní plán. V základních cvičeních však zůstaneme pouze u číselných proměnných, které vesměs budou fungovat jako jednoduché čítače.
Užitečná příprava na práci s proměnnými jsou úlohy, ve kterých programy mění stav zobrazený na plánku – například barvu skřítka nebo přítomnost kamenů. Měněné atributy (barva skřítka, přítomnost kamenů) lze vnímat jako proměnné.
Základní práce s proměnnými zahrnuje přiřazování hodnot do proměnných, změnu hodnoty (zvýšení, snížení), využití proměnné ve výrazech a porovnávání proměnných. Užitečnost proměnných se však naplno projeví až v kombinaci s cykly a podmíněnými příkazy.
NahoruProměnné: základní princip
Proměnná je pojmenované úložiště, které udržuje hodnotu. Proměnná má jméno, pomocí kterého se na ni v programu odkazujeme, a hodnotu, kterou můžeme měnit (proto název „proměnná“). Proměnnou si lze představit jako obálku, na které je napsané jméno a uvnitř má schovanou hodnotu – číslo, které můžeme přepsat na jiné.

Nastavení nové hodnoty
Hodnotu proměnné nastavíme pomocí přiřazovacího příkazu, který se často zapisuje jméno ← hodnota. Příkaz x ← 1 nastaví hodnotu proměnné x na 1. V proměnné je pak uložená pouze poslední přiřazená hodnota, důležité je proto pořadí příkazů:
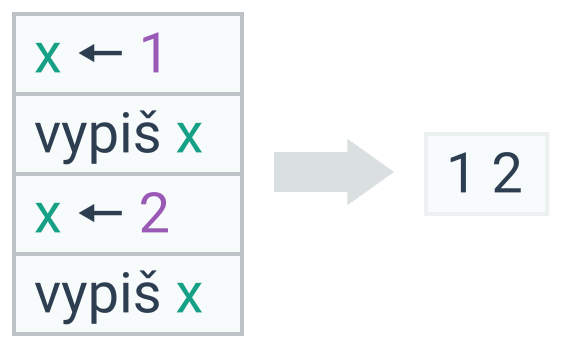
Zápis přiřazovacího příkazu
Různé programovací jazyky využívají odlišné zápisy přiřazovacího příkazu, například nastav x na 3, x ← 3, nebo x = 3. Zápis s rovnítkem (x = 3) může být matoucí, protože v matematice se využívá pro vyjádření rovnosti (nikoliv přiřazení hodnoty). Přesto ho využívá většina dnešních programovacích jazyků, protože je krátký a snadno zapsatelný na klávesnici. K vyjádření rovnosti v podmínkách se pak v těchto jazycích používá většinou dvojité rovnítko (x == 3).
Zvýšení a snížení hodnoty
Pomocí přiřazovacího příkazu můžeme také zvýšit či snížit aktuální hodnotu proměnné. Příkaz x ← x + 1 zvýší hodnotu proměnné x o 1, příkaz x ← x − 2 sníží hodnotu proměnné x o 2.
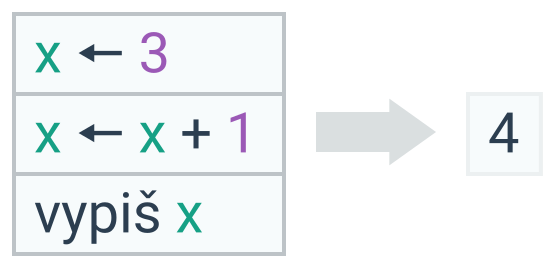
Nejprve se vyhodnocuje výraz na pravé straně (x + 1 = 3 + 1 = 4), výsledek se pak přiřadí do proměnné x.
Použití hodnoty proměnné
Pokud chceme použít hodnotu proměnné, stačí v programu uvést její jméno. Například příkaz vypiš x vypisuje hodnotu, nikoliv jméno proměnné. Proměnnou můžeme použít jako parametr příkazu, například jdi vpřed o x pixelů.
Mýty o proměnných
| Mýtus | Skutečnost |
|---|---|
Proměnná se vždy označuje jménem x. |
Proměnné mohou mít různá jména (např. cena, úhel, barva). |
| V programu může být jediná proměnná. | Program může pracovat s libovolným počtem proměnných. |
| Proměnnou lze použít jen jednou. | Proměnnou lze v programu použít opakovaně. |
| Hodnotu proměnné nelze měnit. (Tj. proměnná je jako neznámá v matematice.) | Hodnotu proměnné lze měnit. |
| Proměnná, do které nebylo nic přiřazeno, má hodnotu 0. | Počáteční hodnota proměnné není určená, je potřeba do ní nějakou hodnotu přiřadit. |
| Proměnná si pamatuje všechny hodnoty, které do ní byly v minulosti přiřazeny. | V proměnné je uložená pouze poslední přiřazená hodnota. |
| Proměnná automaticky sčítá všechny přiřazené hodnoty. | V proměnné je uložená pouze poslední přiřazená hodnota. |
| Použití proměnné (např. výpis) smaže aktuální uloženou hodnotu. | Použití proměnné (např. výpis) nemění hodnotu proměnné. |
Výpis proměnné (vypiš x) vypisuje její jméno. |
Výpis proměnné (vypiš x) vypisuje její hodnotu. |
Proměnné: obecné principy
Proměnná je pojmenované úložiště hodnoty, kterou lze měnit. V úvodní kapitole jsme viděli, jak můžeme měnit hodnotu jedné proměnné. V této kapitole budeme uvažovat i složitější situace, kdy dochází k interakci mezi více proměnnými a je potřeba rozlišovat mezi jménem a hodnotou proměnné.
Jméno vs. hodnota
Proměnná má jméno a hodnotu. Pomocí jména se na proměnnou v programu odkazujeme, když chceme její hodnotu použít nebo změnit. Mezi jménem a hodnotou je vhodné rozlišovat, například v příkazu vypiš x musí být x jméno proměnné, ale vypíše se její hodnota (nikoliv jméno). Pokud chceme kreslit kolečka rostoucí velikosti, použijeme proměnnou se jménem r nebo poloměr, která bude postupně nabývat hodnot 10, 20, 30 atd.
Typ proměnné
Proměnné nemusí být jen čísla. Kromě jména a hodnoty mají proto proměnné ještě typ, což může být například celé číslo, text ("mrkev"), nebo logická hodnota (pravda / nepravda).
Změna hodnoty
Přiřazovací příkaz umožňuje nastavit novou hodnotu proměnné, nebo upravit hodnotu stávající. Příkaz x ← 3 nastaví hodnotu proměnné x na 3, příkaz x ← x + 1 zvýší hodnotu proměnné x o 1. Na levé straně přiřazovacího příkazu je proměnná, kterou měníme, na pravé straně může být konkrétní hodnota, proměnná, nebo libovolný výraz.
Pokud je na pravé straně výraz, nejprve se vyhodnotí a výsledek se nastaví jako nová hodnota proměnné. Příkaz x ← 1 + 1 nastaví hodnotu proměnné x na 2. Výraz na pravé straně může obsahovat proměnné. Příkaz x ← y + 1 nastaví hodnotu proměnné x na hodnotu o 1 vyšší, než je aktuální hodnota y.
Více jmen pro jednu hodnotu
Přiřazovací příkaz x ← y nastaví hodnotu proměnné x na hodnotu proměnné y. Hodnota proměnné y se přitom nemění.
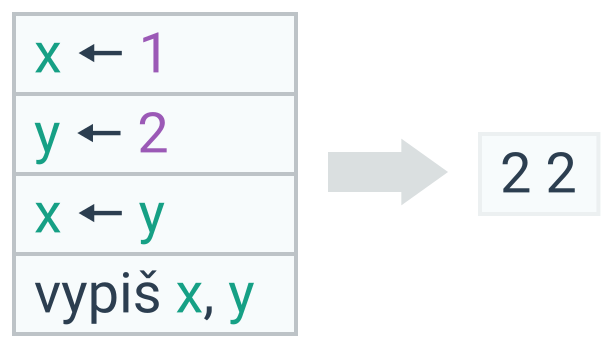
Po provedení přiřazovacího příkazu x ← y mají obě proměnné stejnou hodnotu. Pořád jde však o dvě různé proměnné – pokud do proměnné y přiřadíme novou hodnotu, proměnnou x tím neovlivníme.
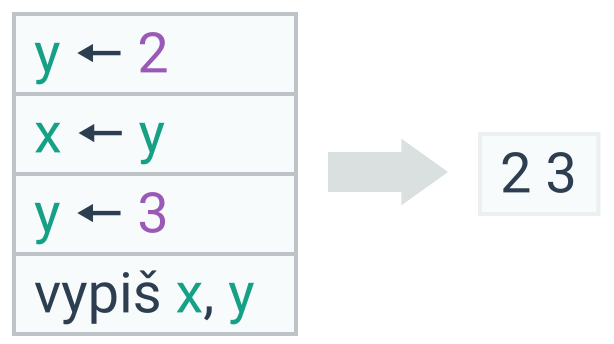
Prohození hodnot proměnných
Po provedení příkazu x ← y mají obě proměnné stejnou hodnotu. K prohození hodnot dvou proměnných je proto potřeba pomocné proměnné. Hodnoty prohodí následující trojice příkazů (pro konkrétnější představu předpokládejme x = 1, y = 2):
p ← x(uložíme si 1 do pomocné proměnné)x ← y(x přenastavíme na 2)y ← p(y přenastavíme na 1)
Mýty o přiřazovacím příkazu
| Mýtus | Skutečnost |
|---|---|
| Proměnná, do které nebylo nic přiřazeno, má hodnotu 0. | Počáteční hodnota proměnné není určená, je potřeba do ní nějakou hodnotu přiřadit. |
| Proměnná si pamatuje všechny hodnoty, které do ní byly v minulosti přiřazeny. | V proměnné je uložená pouze poslední přiřazená hodnota. |
| Proměnná automaticky sčítá všechny přiřazené hodnoty. | V proměnné je uložená pouze poslední přiřazená hodnota. |
Přiřazovací příkaz x ← y přesouvá hodnotu, tj. y pak nemá hodnotu. |
Přiřazovací příkaz x ← y nastaví x, proměnnou y nemění. |
Přiřazovací příkaz x ← y přiřadí do proměnné x text “y”. |
Přiřazovací příkaz x ← y přiřadí do proměnné x hodnotu proměnné y. |
Metafory pro proměnné
Proměnné lze přirovnat třeba ke krabičkám, šuplíkům či obálkám, které mají uvnitř nějaký předmět (nebo třeba číslo napsané na papíře). Trochu přesněji odpovídají proměnným štítky nalepené na předmětech, nebo popsané kolíky držící předměty na prádelní šňůře. Takové metafory mohou přispět k základní intuici za proměnnými, je však potřeba vědět, že každá metafora má svoje omezení a neplatí dokonale.
Proměnné jako krabičky
Proměnná se často přirovnává ke krabičce, která je popsaná (jméno proměnné) a uvnitř má nějaký objekt (hodnota proměnné), třeba jablko. Můžeme se podívat, jaký objekt je uvnitř krabičky (zjištění hodnoty) a můžeme objekt v krabičce nahradit jiným, třeba hruškou (změna hodnoty). Tato metafora má však má svoje limity:
Do skutečné krabičky bychom nejspíš mohli přidat hrušku, aniž bychom z ní odebrali jablko. Proměnná si však pamatuje pouze poslední přiřazenou hodnotu. To by odpovídalo pravidlu, že kdykoliv do krabičky něco dáváme, nejprve ji vyprázdníme.
Ze skutečné krabičky bychom mohli objekt vzít a dát ho do jiné krabičky. To však neodpovídá chování přiřazovacího příkazu
x ← y, po kterém je původní hodnota proměnnéyv obou proměnnýchxiy. To by odpovídalo krabičkám vybaveným magickou kopírkou pro vytváření kopií objektů před jejich přiřazením či jiným použitím.

Proměnné jako nálepky
Proměnné si můžeme představit jako samolepicí štítky (jméno proměnné) nalepené na objektu (hodnota proměnné). Přiřazovací příkaz x ← y odpovídá přelepení nálepky x na objekt označený nálepkou y. Jeden objekt tak může mít více nálepek (jmen), zatímco jedna nálepka se vždy odkazuje na jediný objekt.

Výrazy s proměnnými
Hodnoty a proměnné lze kombinovat do výrazů pomocí operátorů. Například podmínka x + 5 ≥ y obsahuje operátory + a ≥. Většina programovacích jazyků výrazy rovnou vyhodnocuje. Po provedení příkazu x ← 1 + 1 bude v proměnné x číslo 2, nikoliv nevyhodnocený výraz nebo dokonce text 1 + 1.
Aritmetické výrazy
S číselnými hodnotami a proměnnými můžeme počítat pomocí aritmetických operátorů + (sčítání), − (odčítání), * (násobení) a / (dělení). Priorita operací je stejná jako v matematice (tj. násobení a dělení má přednost před sčítáním a odčítáním) a stejně jako v matematice můžeme ovlivnit pořadí vyhodnocení pomocí závorek (např. 1 + 2 * 3 = 7, zatímco (1 + 2) * 3 = 9).
Porovnávání
Číselné hodnoty a proměnné můžeme porovnávat pomocí relačních operátorů < (menší než), ≤ (menší rovno), > (větší než), ≥ (větší rovno), = (rovno), ≠ (nerovno). Výsledkem porovnávání je logická hodnota (pravda/nepravda), kterou můžeme vypsat, ale většinou ji využíváme v rámci podmínek. Relační operátory mají typicky nižší prioritu než aritmetické, tj. napřed se vyhodnotí výrazy na levé a pravé straně relačního operátoru a teprve poté se provede porovnání (např. 1 + 3 < 2 + 4 se nejprve částečně vyhodnotí na 4 < 6, což je pravda).
Relační operátory v programovacích jazycích
Různé programovací jazyky využívají odlišné zápisy některých operátorů, často proto, aby se daly snadno napsat na klávesnici. Běžné je například x >= 3 místo x ≥ 3 a x != 3 místo x ≠ 3. Pro rovnost se typicky využívají dvě rovnítka (x == 3), protože jedním rovnítkem (x = 3) se často zapisuje přiřazovací příkaz.
Operace s textem a logickými hodnotami
Programovací jazyky nabízí i operátory pro práci s dalšími datovými typy než jen s čísly. Například textové řetězce lze lexikograficky porovnávat (tj. znak po znaku abecedně, např. "ab" < "ac") a spojovat ("ab" + "ac" = "abac"). Logické hodnoty (zejména tedy výsledky porovnávání) lze kombinovat pomocí logických operátorů (spojek) a, nebo a neplatí, což se hodí pro vytváření složitějších podmínek. Logické operátory si můžete procvičit jako samostatné téma.
Použití výrazů s proměnnými
Výrazy s proměnnými se mohou vyskytovat např. na pravé straně přiřazovacího příkazu, v podmínkách a výpisech:

Cykly s proměnnými
Během opakování příkazů se nám někdy hodí vědět, v kolikátém opakování (iteraci) právě jsme. K tomu lze využít následující konstrukci, v programovacích jazycích označovanou jako for cyklus:
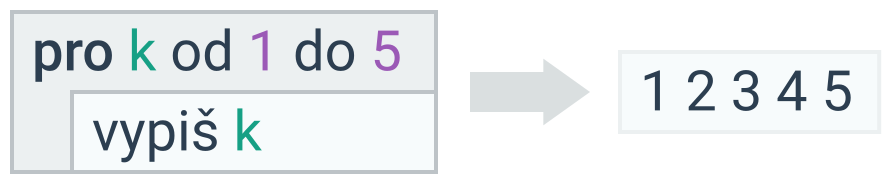
Proměnnou, která se během cyklu automaticky mění (v tomto případě označenou k) nazýváme řídící proměnná cyklu. Řídící proměnné lze využít v libovolných výrazech uvnitř cyklu. For cykly lze do sebe vnořovat. Všimněte si pořadí, ve kterém se řídící proměnné mění:

Proměnné lze využít také v rámci podmínek cyklu opakuj dokud:
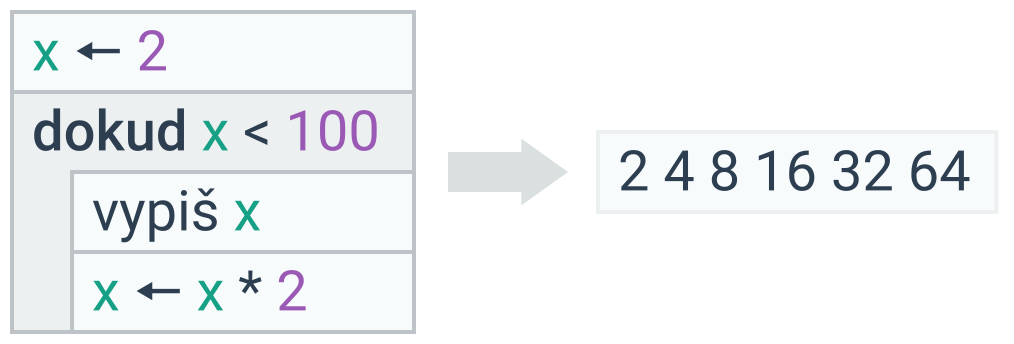
V tomto případě si musíme dávat obzvlášť pozor na zacyklení – situaci, kdy podmínka cyklu nikdy nepřestane platit a cyklus se tedy bude opakovat donekonečna. To se může stát například tehdy, když zapomeneme v těle cyklu měnit hodnotu proměnné, která figuruje v podmínce, když příkaz měnící proměnnou chybně odsadíme (takže nebude součástí cyklu), nebo když nevhodně formulujeme podmínku tak, že nepřestane platit navzdory změně proměnné:
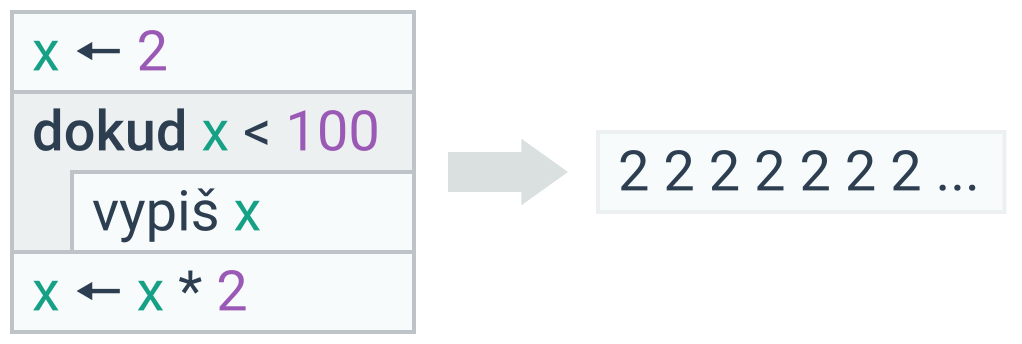
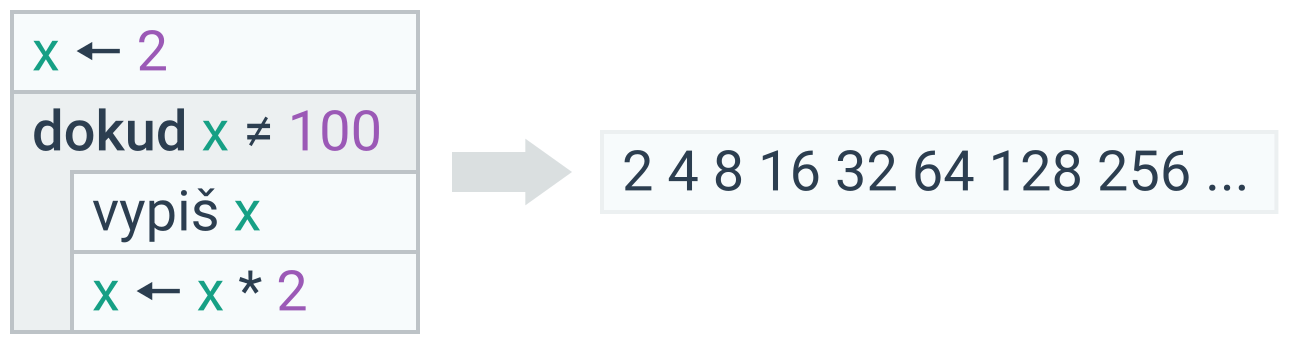
Podmínky s proměnnými
Podmínky často obsahují proměnné:

To je užitečné například uvnitř cyklů nebo funkcí:
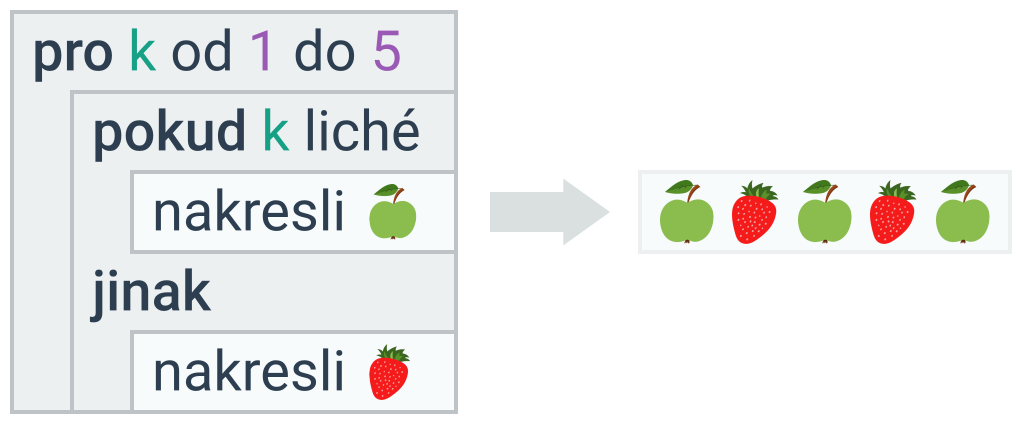
Při vyjadřování podmínek často využíváme logické spojky (a zároveň, nebo, negace):

Složitější podmínky, které využíváme opakovaně, je vhodné pojmenovat. K tomu lze využít logické proměnné, které mají hodnotu pravda nebo nepravda. V následujícím kódu zavádíme logickou proměnnou shoda, která má hodnotu pravda, pokud je x rovno některé z hodnot p nebo q:

Typy proměnných
Každá proměnná má svůj datový typ. Datový typ určuje, jaké hodnoty může proměnná obsahovat a které operace s ní lze provádět. Některé programovací jazyky požadují, aby byl typ proměnné uveden v programu, jiné odvozují typ automaticky podle přiřazené hodnoty. Programovací jazyky se liší také v tom, které datové typy nabízejí. Mezi nejběžnější datové typy patří:
- celé číslo (
123,−7) – s čísly lze provádět aritmetické operace (1 + 2) a porovnávat je (1 < 2) - desetinné číslo (
1,23,–0,05) – typicky se používá tzv. „pohyblivá řádová čárka“, což umožňuje ukládat i velmi velká nebo malá čísla, ale s omezenou přesností (např. s 5 platnými číslicemi lze uložit 123 450 000 i 0,000 012 345, nikoliv však 123,456) - logická (pravdivostní) hodnota (
pravda,nepravda) – reprezentuje informaci o pravdivosti, lze s nimi provádět logické operace (neplatí x,x nebo y,x a y). (Tento typ se často označuje jako „bool“ nebo „boolean“ podle George Boola, který popsal pravidla pro výpočty s logickými hodnotami.) - textový řetězec (
“slovo”,“více slov”) – reprezentuje text libovolné délky. Pro odlišení od názvů proměnných se typicky vymezují pomocí “uvozovek” či ‘apostrofů’. Je potřeba rozlišovat mezi řetězcem obsahujícím číslo a číslem –“123”není123. (Tento typ se často označuje jako „string“, z anglického slova pro řetězec.) - seznam (pole) (
[1, 2, 3],[‘x’, ‘y’, ‘z’]) – umožňuje uložit více souvisejících hodnot do jedné proměnné. (Často jsou k dispozici i další typy pro ukládání různých kolekcí dat.)
Existují další typy pro specifické účely (např. čas, datum, soubor). Většinou je také možné definovat si vlastní typy. Výčtový typ umožňuje definovat proměnné, které mohou nabývat pouze několika předem určených hodnot (např. světový směr, den v týdnu). Záznamy umožňují definovat složené proměnné, které se skládají z několika pojmenovaných položek (např. záznam o zákazníkovi by mohl obsahovat jeho jméno, věk a datum posledního nákupu).
NahoruPojmenování proměnných
Jména proměnných neovlivňují chování počítače při vykonávání programu, jsou však důležitá pro čitelnost kódu. Pokud pojmenujeme proměnnou celková_cena, neznamená to, že v ní bude automaticky uložený součet cen položek (to musíme zajistit vhodnými příkazy), je ale jasnější, co má proměnná reprezentovat, než když ji pojmenujeme c.
Velikost písmen hraje roli
Většina programovacích jazyků rozlišuje velká a malá písmena ve jménech, např. Cena a cena jsou dvě různé proměnné.
Povolená jména
Proměnné nelze pojmenovat libovolně. Konkrétní omezení se mezi programovacími jazyky mírně liší. Typická omezení jsou následující:
- Jména mohou obsahovat pouze písmena, číslice a podtržítka. Kdyby se proměnná jmenovala
a+b, nešlo by ji odlišit od operace sčítání. Číslicí ale nesmí jméno začínat. Kdyby se proměnná jmenovala12, nešlo by ji odlišit od hodnoty12. - Jména nemohou obsahovat mezery. Kdyby se proměnná jmenovala
cena mrkve, nešlo by snadno poznat, zda nejde o dvě proměnné (cenaamrkve). Pokud chceme více slov, můžeme použít například podtržítko (cena_mrkve). - Jako jméno nelze použít tzv. „rezervovaná slova“, které už mají v programovacím jazyce určený význam (např.
opakuj,nebo,pravda).
Povolená jména v blokových jazycích
V blokových programovacích jazycích, které mají samostatný blok pro proměnnou, tato omezení být nemusí (protože je jasné, že jde o jméno proměnné a kde toto jméno začíná a končí).
Konvence
Různé programovací jazyky mají navíc různé konvence, které podporují jednotnost kódu. Například v jazyce Python se jména proměnných píší malými písmeny, anglicky a více slov se odděluje podtržítkem (např. car_speed). Jde však pouze o doporučení – program se spustí, ať konvence dodržujeme, nebo nikoliv.
Konvence pro víceslovné proměnné
Různé programovací jazyky mají například různé konvence, jak psát jména proměnných obsahující více slov. Používané možnosti jsou následující:
- vynechání mezer (
cenamrkve) - nahrazení mezer podtržítky (
cena_mrkve) – tzv. „hadí_notace“ - nahrazení mezer spojovníky (
cena-mrkve) – tzv. „špízová-notace“ (méně časté, protože spojovník se používá pro odčítání) - vynechání mezer a označení začátků slov velkým písmenem (
cenaMrkve, příp.CenaMrkve) – tzv. „velbloudíNotace“ (velká písmena ve jméně připomínají hrby velblouda)
Popisnost
Popisná jména výrazně usnadňují čitelnost programu a snižují riziko chyb. Příkaz celková_cena ← cena_mrkev_1kg * kg_mrkve je jasnější než cena ← c * m a je také jasnější, že jsou správně jednotky. Volíme taková jména, která jednoznačně vyjadřují účel proměnné, i za cenu delšího názvu. Jednopísmenné názvy (např. x) jsou vhodné jen v omezených případech (řídící proměnná cyklu, souřadnice bodu, krátké ukázky kódu).
Další doporučení
- Používat jména, která lze dobře vyslovit.
- Nepoužívat zkratky (s výjimkou všeobecně známých).
- Nemít v programu dvě jména, která se liší jen jedním znakem.
- Nemít v programu dvě jména, která se podobně vyslovují.
- V rámci jednoho kontextu nepoužívat jedno jméno pro více různých věcí (ani v případě, že se už na původní proměnnou odkazovat nepotřebujeme).
Použití proměnných
Proměnné se hodí k různým účelům. Většina proměnných má jednu z následujících rolí:
Fixní hodnota (pojmenovaná konstanta)
Proměnná, jejíž hodnota se po inicializaci (prvním přiřazení) už nemění.

Procházení hodnot (aktuální hodnota, počítadlo)
Proměnná drží poslední hodnotu během procházení nějaké předem dané posloupnosti hodnot (např. všech čísel od 1 do 10).

Poslední hodnota (načítání vstupu, generování čísel)
Proměnná drží poslední získanou hodnotu. Např. načítáme vstup od uživatele, dokud nezadá kladné číslo, nebo hážeme kostkou, dokud nepadne sudé číslo. Na rozdíl od „procházení hodnot“ zde neznáme hodnoty dopředu.

Předchozí hodnota
Proměnná, která následuje hodnoty jiné proměnné – pamatuje si její předchozí hodnotu. V následujícím programu si proměnná p pamatuje předchozí hodnotu proměnné x, abychom mohli vypisovat rozdíly mezi načítanými čísly.

Nejlepší hodnota
Proměnná drží nejlepší hodnotu při procházení posloupnosti hodnot („nejlepší“ podle nějakého kritéria, např. nejmenší, největší). V následujícím programu si proměnná m pamatuje nejvyšší načtené číslo.

Příznak (jednocestný spínač)
Pojem „příznak“ se používá obecně pro proměnnou, která může nabývat jen dvou hodnot (typicky pravda / nepravda). O „jednocestný spínač“ jde v případě, kdy se proměnná už nikdy nevrátí do původního stavu, jakmile je jednou změněná. V následujícím programu si proměnná p pamatuje, zda některé načtené číslo přesáhlo 100. Jakmile se jednou p nastaví na pravda, už se nikdy nezmění.

Akumulátor (souhrn hodnot)
Proměnná akumuluje (shrnuje) procházené hodnoty do jedné (např. součet). V následujícím programu proměnná s akumuluje součet zadaných hodnot. („Nejlepší hodnotu“ i „jednocestný spínač“ lze vnímat jako speciální případy akumulátoru, kdy shrnutím posloupnosti hodnot je nejlepší hodnota, resp. příznak.)

Transformace (přímý výpočet)
Proměnná je přímou transformací jiné proměnné. V následujícím programu je proměnná m druhou mocninou proměnné x.

Pomocná proměnná (dočasná proměnná)
Jako „pomocné“ označujeme takové proměnné, které drží hodnotu jen na velmi krátký čas (a nemají žádnou z jiných konkrétnějších rolí popsaných výše). V následujícím programu si do pomocné proměnné p dočasně ukládáme původní hodnotu x, abychom mohli prohodit hodnoty proměnných x a y.

Jedna proměnná může svoji roli v průběhu programu změnit, většinou je však vhodnější pro nový účel použít novou proměnnou.
NahoruFunkce a zobecňování
Funkce jsou základním stavebním blokem, pomocí kterého vytváříme programy. Představují konkrétní realizaci obecného principu rozklad na části.
Zjednodušeně řečeno, funkce je kouzlo, kterému něco předložíme (vstup) a ono nám vykouzlí něco jiného (výstup).
- Pohádkový příklad: Zvětšovací kouzelná hůlka, kterou poťukáme zeleninu a ona ji zvětší na dvakrát větší velikost.
- Matematický příklad: Funkce odmocnina, která dáme na vstup číslo a ona nám vrátí jiné číslo (např. pro vstup 25, vrátí výsledek 5).
- Programátorský příklad: Funkce
polygon(n, délka), které dáme na vstup dvě čísla (počet stran a délku strany) a ona vykreslí obrázek mnohoúhelníku.
Jednoduché funkce bez parametrů umožňují pouze opakované vykonání přesně téhož kódu (např. vždy stejně velký čtverec). Funkce však mohou obsahovat i parametry, které ovlivňují jejich chování (např. velikost čtverce). Funkce mohou volat jiné funkce a někdy dokonce samy sebe – takovým funkcím se říká rekurzivní.
Při zavádění funkcí potřebujeme umět abstrahovat – tedy odhlédnout od nepodstatných detailů – a následně kód zobecnit – tedy nahradit proměnlivé detaily proměnnými, z nichž pak uděláme parametry funkce. Složitý program, zejména takový, ve kterém se opakuje podobný kód, lze rozložit do několika funkcí, a tím ho zjednodušit a zpřehlednit.
NahoruAbstrakce
Abstrakce je schopnost odhlížet od detailů, které nejsou důležité pro řešení zkoumaného problému. Soustředíme se na společné prvky a vlastnosti, pomocí kterých nacházíme obecnější řešení.
Příklad z běžného života: Alík, Ben a Rex jsou tři konkrétní domácí zvířata. Můžeme je označit abstraktním pojmem „pes“ – tím zanedbáváme řadu jejich vlastností (např. stáří, barvu srsti či rasu) a soustředíme se jen na to, co mají společné. Kdybychom měli doma ještě kocoura Mourka, tak bychom mohli pro jejich společné označení použít třeba kategorii „savec“.
Příklad z programování: Při vykreslování obrázků můžeme vytvořit funkci squareA(), která vykreslí modrý čtverec o velikosti 100, a squareB(), která vykreslí žlutý čtverec o velikosti 200. Lepší je ale vytvořit abstraktnější funkci square(length, color), která vykreslí čtverec libovolné velikosti a barvy (podle zadaných parametrů). Případně můžeme v abstrakci pokračovat dál a vytvořit funkci, která vykreslí libovolný mnohoúhelník (se zadaným počtem vrcholů).
Funkce bez parametrů
Funkce je pojmenovaný blok kódu, který slouží k provedení nějakého úkolu (např. výpočtu obsahu, nakreslení čtverce). Funkci provedeme (tzv. „zavoláme“) jejím jménem:

Funkce v programování a matematice
Funkce v programování a v matematice jsou podobné koncepty. Funkce v matematice (např. druhá mocnina) předepisuje, jak se nějaká hodnota změní na jinou (např. 3 → 9). Podobně funkce v programování může provádět výpočty (např. počítat druhou mocninu), může ale také třeba něco vykreslit nebo vypsat. Druhý rozdíl spočívá v tom, že součástí definice funkce v programování musí být přesný postup (posloupnost kroků), jak výsledku dosáhnout. (Některé matematické funkce přitom nelze spočítat žádným programem.)
Funkce ve Scratchi
I ve Scratchi si můžete definovat vlastní funkce (nové bloky). Označují se jako scénáře a najdete je v sekci Moje bloky.
Definice a volání funkce
Definice funkce zahrnuje její jméno a tělo – blok kódu, který se má provést, když funkci zavoláme. Funkce se neprovede při její definici, ale až poté, co ji zavoláme. Funkci definujeme jednou a můžeme ji pak volat opakovaně.
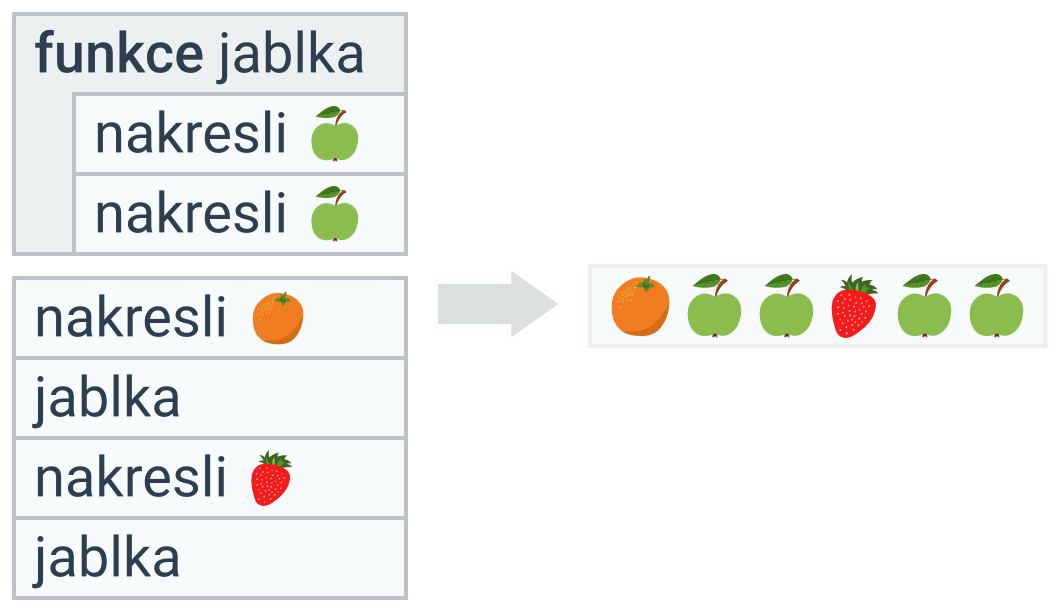
Funkce mohou obsahovat i parametry, které ovlivňují jejich chování (např. velikost čtverce), v této kapitole se však omezíme na jednoduché funkce bez parametrů.
Využití funkcí
Funkce nám umožňují definovat si vlastní příkazy (bloky), nebo využít příkazy, které napsal někdo jiný. Pokud řešíme složitý problém, můžeme ho zjednodušit rozložením na podproblémy, které vyřešíme zvlášť – každý podproblém pomocí jedné funkce, která je jednodušší než program pro celý problém. Pokud se nám v programu opakuje podobný kód, můžeme ho zavedením funkce pro opakující se úsek kódu zkrátit. Kód, který je strukturovaný do funkcí a který neobsahuje podobný kód na více místech, se pak snáze čte, opravuje a rozšiřuje.
NahoruFunkce s parametry
Funkce mohou mít parametry, které ovlivňují jejich chování. To se hodí pro psaní obecných funkcí, které budou použitelné ve více případech – různé hodnoty parametrů povedou na různé chování. Parametry se většinou zapisují do závorek za jméno funkce. Když funkci voláme, musíme dodat hodnoty parametrů (opět typicky v závorkách za jménem funkce).
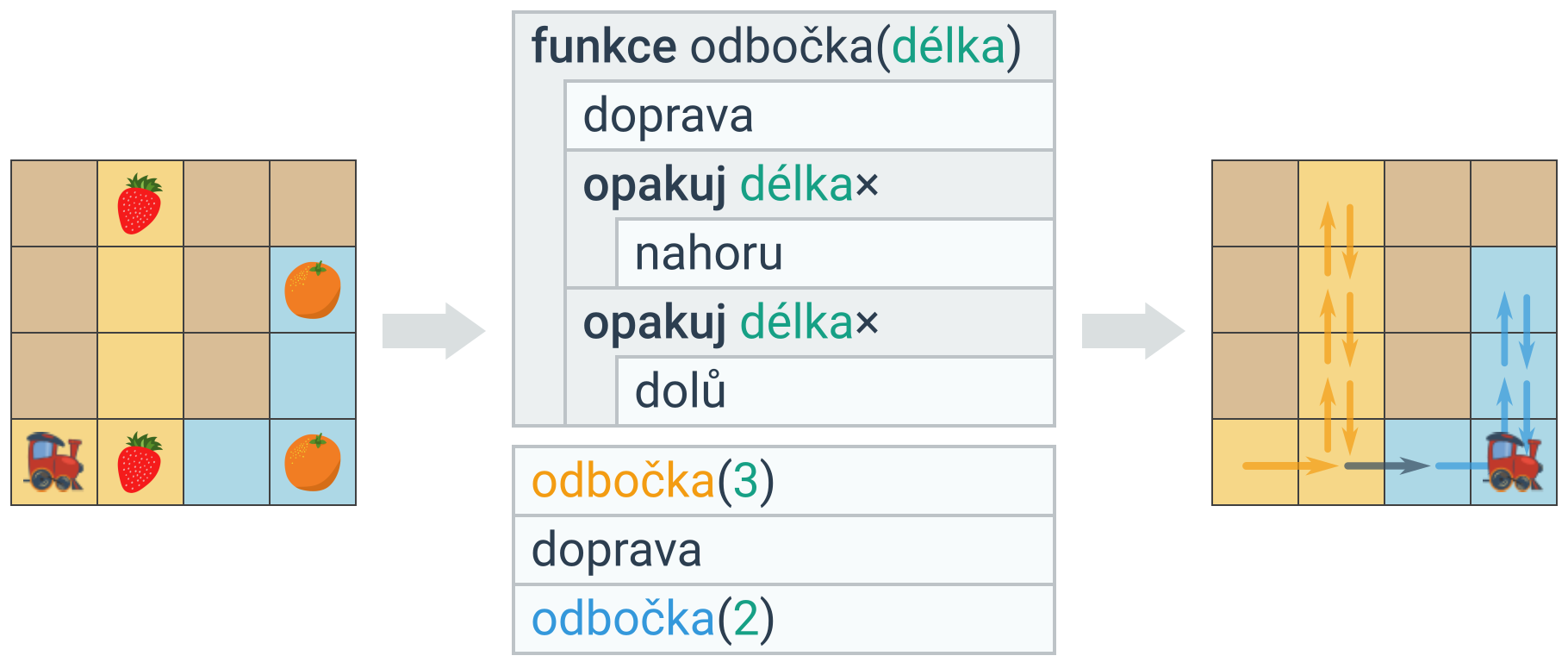
Parametry funkce lze vnímat jako speciální proměnné. Předaným hodnotám parametrů se říká argumenty. (V ukázce výše je parametrem jméno délka, zatímco čísla 3 a 2 argumenty.)
Parametry ve Scratchi
Scratch označuje funkce jako „scénáře“ či „moje bloky“ a umožňuje jim přiřadit parametry různých typů – číslo, text, logická hodnota (pravda/nepravda).
Více parametrů
Funkce může mít parametrů více. Oddělují se většinou čárkou. První parametr se nastaví na první předaný argument, druhý parametr na druhý předaný argument atd. V následující ukázce se nastaví n = 5, x = 3 a vypíše se pět trojek. Pokud bychom volali řada(3, 5) nastavilo by se n = 3, x = 5 a vypsaly by se tři pětky.

Funkce s návratovou hodnotou
Funkce mohou vracet vypočtenou hodnotu pomocí klíčového slova vrať. Takové funkce pak lze využít v rámci výrazů, resp. všude, kde se očekává nějaká hodnota. V následující ukázce lze využít funkci mocnina při volání funkce smích, protože mocnina(3) vrací hodnotu 9. Kdyby funkce mocnina výsledek vypisovala, ale nevracela, nebylo by toto možné.
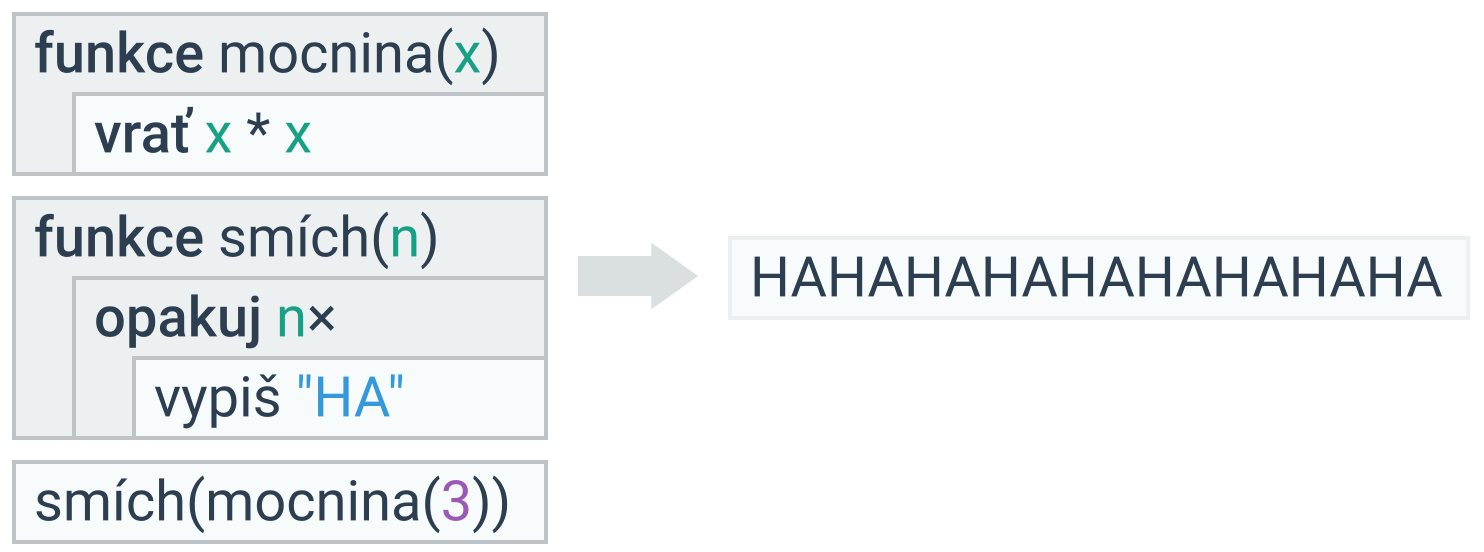
Funkce vs. procedury
Někdy se rozlišuje mezi funkcemi, které vrací hodnotu, a procedurami, které nic nevrací. Obecný název pro funkce a procedury je pak podprogram. Často se však mezi těmito případy nerozlišuje a používá se pouze pojem „funkce“.
Zobecňování programů
Programy lze často zobecnit (abstrahovat) nahrazením konkrétní hodnoty za obecnou proměnnou. To umožňuje tvořit programy, které řeší obecnější problémy. Například místo několika různých programů pro výpis čísla obklopeného jedničkami stačí jediný: 

Při zobecňování je někdy potřeba kromě proměnné zavést také podmíněný příkaz nebo cyklus. Příklad:


Kromě vytváření obecnějších řešení můžeme pomocí zobecňování upravovat programy tak, aby byly přehlednější. Když si v programu všimneme opakujícího se vzoru (např. opakované výpisy čísla obklopeného jedničkami), můžeme tyto kousky kódu po vhodném zobecnění nahradit společnou funkcí (parametrizovanou proměnnými zavedenými při zobecňování).
NahoruRozklad programů
Složitý program lze zpřehlednit tím, že ho rozdělíme na několik částí, které vyčleníme do samostatných funkcí. V takovém programu se navíc snáze hledají a opravují chyby, protože můžeme testovat jednotlivé funkce zvlášť.
Příklad: V následujícím programu je výpis posloupnosti 11–14 podobný výpisu posloupnosti 31–34. V obou případech jde o výpis 4 čísel od n+1 do n+4. Můžeme proto tyto výpisy nahradit voláním nové funkce s parametrem n, která bude vypisovat n+1 až n+4.


Program rozdělujeme tak, aby nově zavedené funkce měly jasný význam. Často pomůže všimnout si částí programu, které si jsou hodně podobné (hledání vzorů). Tyto části zobecníme tak, aby je vykonával stejný kód a ten zapíšeme do nové funkce (jejími parametry jsou proměnné potřebné ke společnému zobecnění kódů). Původní kódy pak nahradíme voláním této nové funkce.
NahoruRekurze je využití sebe sama. Příkladem je použití pojmu při jeho vlastní definici nebo obrázek obsahující svoji zmenšenou kopii. Rekurzivní funkce je taková funkce, která pro výpočet využívá sebe sama (s jinými hodnotami parametrů). Využití rekurze často vede k elegantnímu řešení problému. Některé programovací jazyky využívají rekurzi jako základní prostředek pro opakování příkazů (místo cyklů).
Faktoriál – příklad rekurzivní definice
Faktoriál čísla n (značí se n!) je součin čísel 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n. Například 4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24. Faktoriál lze definovat rekurzivně:
0! = 1
n! = n \cdot (n - 1)! \text{ pro } n > 0
Nejedná se o definici v kruhu, protože při aplikování definice dochází ke zjednodušování (faktoriál n je definován pomocí faktoriálu n - 1) a je definován i bázový případ (n = 0) bez rekurze, ke kterému vše směřuje. Jde tedy spíše o definici ve spirále.
Rekurzivní šroubování žárovky
A: Kolik otoček potřebuji na zašroubování žárovky?
B: Pokud už je zašroubovaná, tak 0. Jinak ji zatoč jednou, zeptej se mě znova a k mé odpovědi přičti 1.
Návrh rekurzivních algoritmů
Nejprve určíme podproblémy, které potřebujeme k vyřešení našeho problému (např. pro výpočet faktoriálu n potřebujeme znát faktoriál n - 1). Tyto podproblémy vyřešíme rekurzivně (tedy voláním funkce s jinými parametry) a z výsledků poskládáme výsledné řešení. Dále je nutné určit bázový případ a jeho řešení (např. faktoriál 0 je 1). Bázový případ musí být takový, aby se k němu všechny větve výpočtu časem dostaly, jinak by výpočet nikdy neskončil.
Sebe-reference
Rekurze je příkladem obecnějšího jevu odkazování na sebe sama, tzv. sebe-reference. Sebe-reference se vyskytuje v jazyce (Třeba tato věta mluví sama o sobě.), knihách, divadle, filmu i matematice. Sebe-reference je dokonce hlavní ingrediencí snad nejslavnějších důkazů matematiky (Gödelovy věty o neúplnosti) a také informatiky (existence problémů, pro které neexistuje algoritmus, který by je řešil – např. úloha určit, zda daný program někdy zastaví).
Fraktály
Vedle rekurze jsou nejtypičtějším zástupcem sebe-reference fraktály – obrázky, které jsou soběpodobné, tedy jejich části připomínají obrázek jako celek. Fraktály lze často vidět v přírodě (např. větve stromů, kapradina). Fraktály a rekurze nejsou dva nezávislí reprezentanti sebe-reference, i mezi nimi je silná souvislost. Rekurze je totiž velmi elegantní způsob, jak různé fraktály definovat. Díky tomu často můžeme složité fraktály vykreslit pomocí jednoduchých rekurzivních funkcí.
NahoruLadění, hledání chyb
Jen málokdy napíšeme napoprvé bezchybný kód. Riziko chyb snižuje snaha o kvalitní kód, chybám se ale zcela nevyhneme, proto je potřeba chyby aktivně hledat. Chyby v kódu se někdy označují anglickým termínem bug. Proces ověřování správnosti kódu nazýváme testování, proces zjišťování příčiny chyby a její odstranění nazýváme ladění (někdy též „debugování“, angl. „debugging“).
Typy chyb
Rozlišujeme chyby syntaktické (chybný zápis programu – program nelze spustit) a sémantické (program se vykoná, ale nesplňuje požadované chování). Speciálním případem sémantické chyby je zacyklení (program se nikdy nezastaví, např. protože podmínka cyklu nikdy nepřestane platit).
Příklady chyb
Několik příkladů častých sémantických chyb:
- prohození pořadí příkazů (např. pořadí zatáčení a posunu vpřed)
- chybný počet opakování cyklu
- chybné vymezení těla cyklu (např. chybí odsazení příkazu, který se má opakovat)
- záměna cyklu a podmíněného příkazu (
dokudmístopokud) - záměna ostré a neostré nerovnosti (
x < ymístox ≤ y) - záměna logické spojky (
P a QmístoP nebo Q) - prohození srovnávaných proměnných (
x < ymístoy < x) - prohození přiřazované proměnné a hodnoty (
x ← ymístoy ← x) - záměna proměnných (použití chybné proměnné, hrozí zejména při nevhodném pojmenování)
- použití špatného typu proměnné (řetězec
“3”místo čísla3) - chybná hodnota parametru (např. nesprávný úhel, o který je potřeba zatočit)
- záměna argumentů při volání funkce (
f(a, b)místof(b, a)) - záměna výpisu a vrácení z funkce (
vypišmístovrať)
Znalost běžných chyb umožňuje zaměřit při ladění pozornost na místa, kde by se mohla chyba ukrývat.
Postup při ladění programu
Pokud program nevrací správné výsledky, spustíme si ho krok po kroku a sledujeme, kdy se odchýlí od našeho očekávání. Pokud program netvoří grafický výstup, lze si hodnoty proměnných průběžně vypisovat, nebo použít nástroj, který umožňuje program krokovat a sledovat hodnoty proměnných (tzv. debugger). Místo v programu, kde se program odchyluje od našeho očekávání, zkusíme upravit.
Tipy k ladění programů
- Po každé úpravě je vhodné program znovu spustit, abychom si ověřili efekt úpravy.
- Pokud není jasné, jak přesně kód upravit (např. o jaký úhel zatočit), může pomoct nakreslit si obrázek.
- Pokud není jasné, proč se v nějakém bodě program chová určitým způsobem, je lepší to nejprve pochopit, než začneme dělat změny.
- Pokud si nejsme jistí, co dělá některá použitá jazyková konstrukce (příkaz, operátor), vyhledáme si její chování na internetu a ověříme naše porozumění vyzkoušením jednoduchého kódu s danou konstrukcí.
- Pokud je kód zbytečně složitý nebo používá nevhodná jména proměnných, může být po odstranění těchto nedostatků (např. přejmenování proměnných) chyba zjevná.
- Rozložení do funkcí usnadní hledání chyby – můžeme totiž testovat jednotlivé funkce izolovaně.
Úprava programů
Kvalitní kód je takový, který se snadno čte, testuje a upravuje. Kvalitu kódu je vhodné průběžně vylepšovat opravami následujících problémů.
Nepoužitý kód
Části kódu, které se buď neprovedou, nebo sice provedou, ale nijak neovlivňují jeho chování, zbytečně komplikují pochopení programu a je proto vhodné je odstranit. Zbytečný může být příkaz, cyklus, podmínka, proměnná i celá funkce.
Příkaz bez efektu
Efekt nemá opakované přiřazení stejné hodnoty (např. nastavení aktuální barvy malující želvy), přiřazení hodnoty do proměnné, se kterou se již dále nepracuje, nebo matematické operace, které nemění hodnotu (přičtení 0, vynásobení 1).
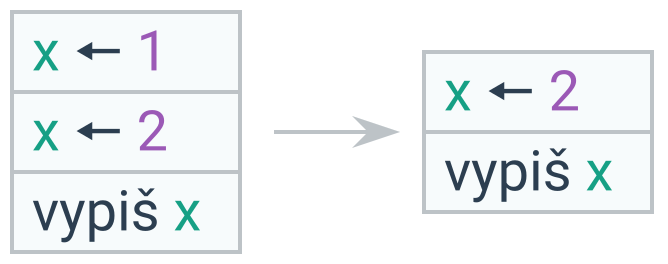
Cyklus provedený jednou/vůbec
Pokud se cyklus provede vždy právě jednou, není potřeba – nedochází k žádnému opakování. Cyklus odstraníme, ponecháme však příkazy, které byly v jeho těle. Pokud se tělo cyklu neprovádí vůbec, lze cyklus odstranit včetně jeho obsahu. Obě tyto situace jsou nejsnáze vidět u cyklu opakuj N×, ale mohou nastat u všech typů cyklů.
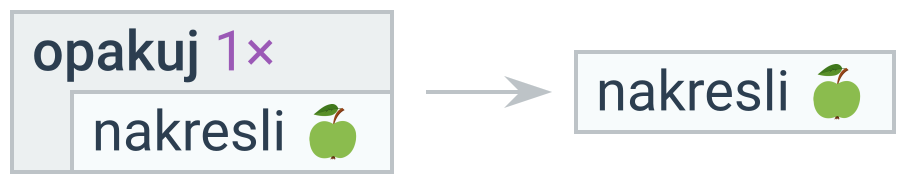
Podmínka platící vždy/nikdy
Pokud podmínka platí vždy, nahradíme podmíněný příkaz obsahem větve pokud. Pokud podmínka neplatí nikdy, nahradíme ho obsahem větve jinak (pokud větev jinak nemá, tak celý podmíněný příkaz smažeme).
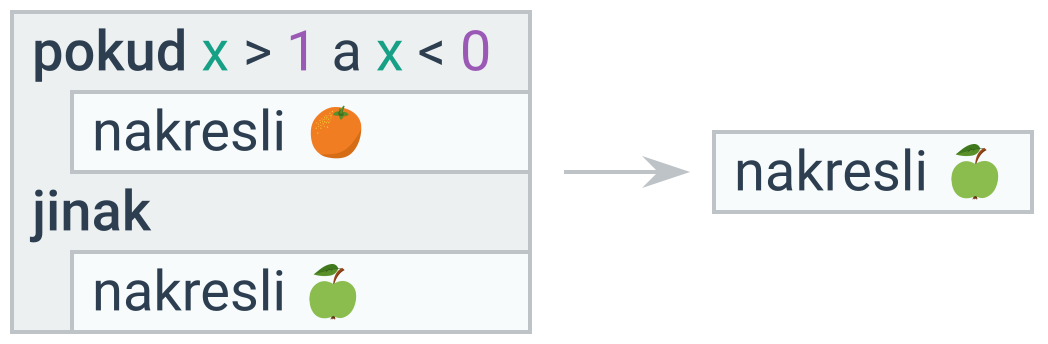
Prázdná větev podmíněného příkazu
Pokud větev jinak neobsahuje žádný příkaz, lze ji vypustit.
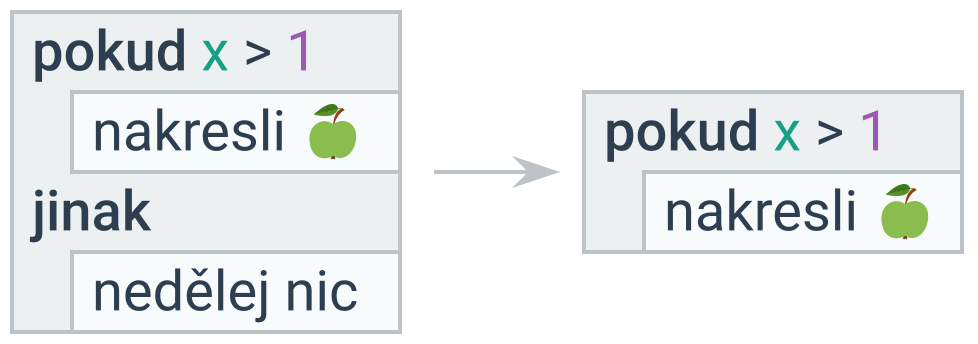
Pokud neobsahuje žádný příkaz první větev, lze větve prohodit (a prázdnou vypustit) negací podmínky.
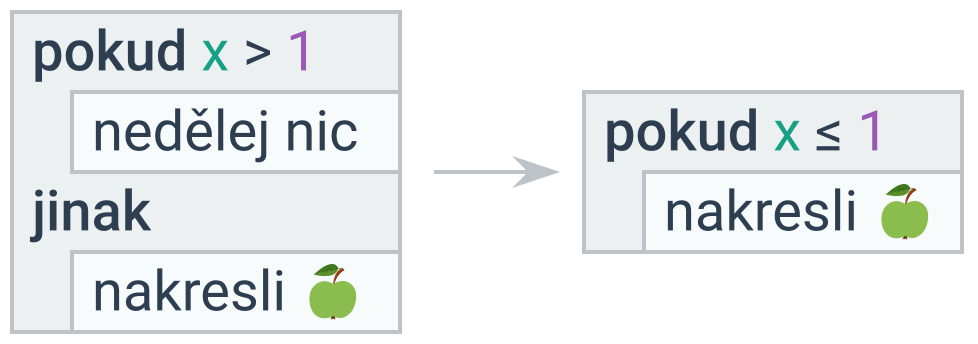
Nepoužitá proměnná
Proměnná, do které se pouze zapisují hodnoty, ale nikdy se z ní hodnota nečte, nemá na běh a výstup programu žádný vliv a lze ji tedy odstranit.
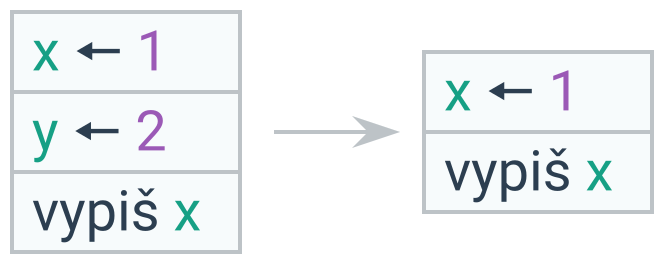
Nezavolaná funkce
Funkce, kterou pouze definujeme, ale nikde nevoláme, je zbytečná a lze ji odstranit.
Zbytečně složitý kód
Pokud lze kód zjednodušit, zvýší to většinou jeho čitelnost. Relativně jednoduché jsou případy, kdy lze sloučit dva příkazy, cykly, nebo podmínky. Kód lze ale také někdy zjednodušit použitím vhodnější programovací konstrukce (např. cyklu opakuj N× místo opakuj dokud) nebo rozkladem programu (zavedením pomocných funkcí).
Sloučitelné příkazy
Sloučení dvou po sobě jdoucích akcí do jedné. Například dvě otočení o 90° a 30° lze nahradit jediným otočením o 120°.
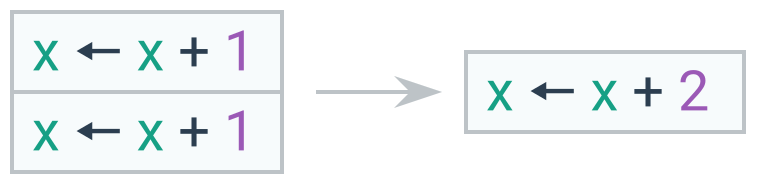
Sloučitelné cykly
Pokud je v těle cyklu pouze vnořený cyklus, lze je sloučit do jediného. Sloučení lze také provést u dvou bezprostředně následujících cyklů, které mají stejné tělo.
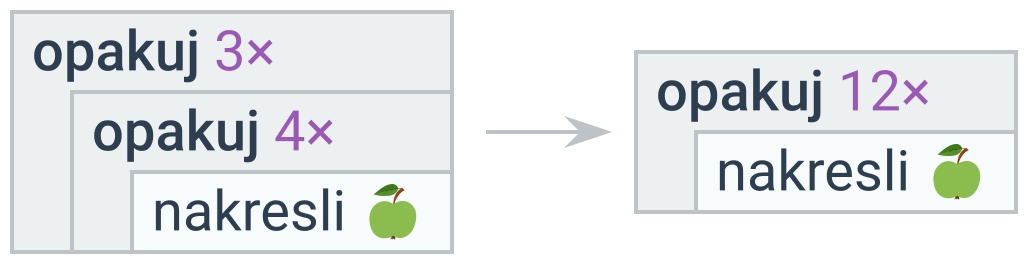
Sloučitelné podmínky
Pokud podmíněný příkaz obsahuje ve svém těle pouze další podmíněný příkaz, lze se vyhnout vnoření použitím složené podmínky.
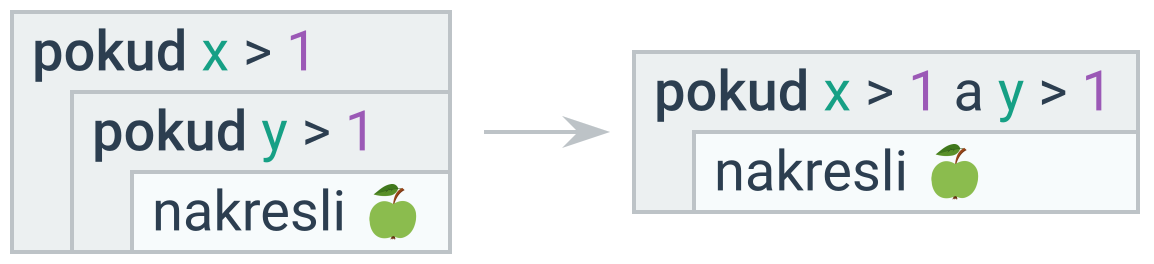
Sloučit lze také dva podmíněné příkazy s opačnou podmínkou (pomocí úplného podmíněného příkazu).
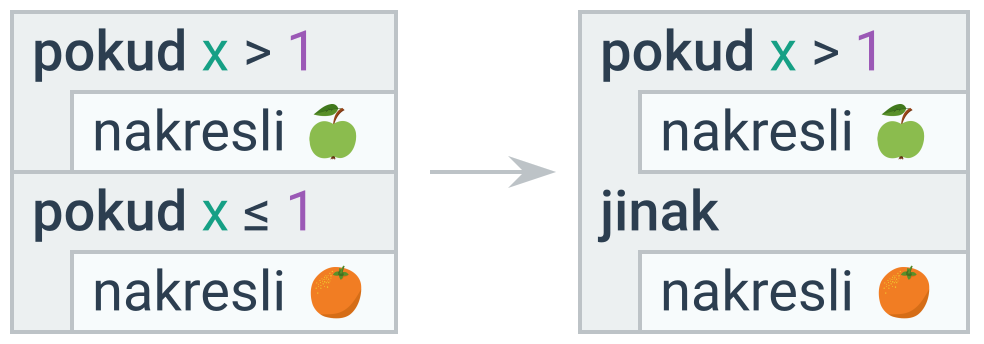
Zjednodušitelná negace
Pokud lze logické výrazy zjednodušit, je to typicky vhodné udělat. Častým případem je aplikace negace na nerovnost nebo složenou podmínku. (V případě úplného podmíněného příkazu lze alternativně prohodit příkazy ve větvích pokud a jinak a negaci vypustit.)
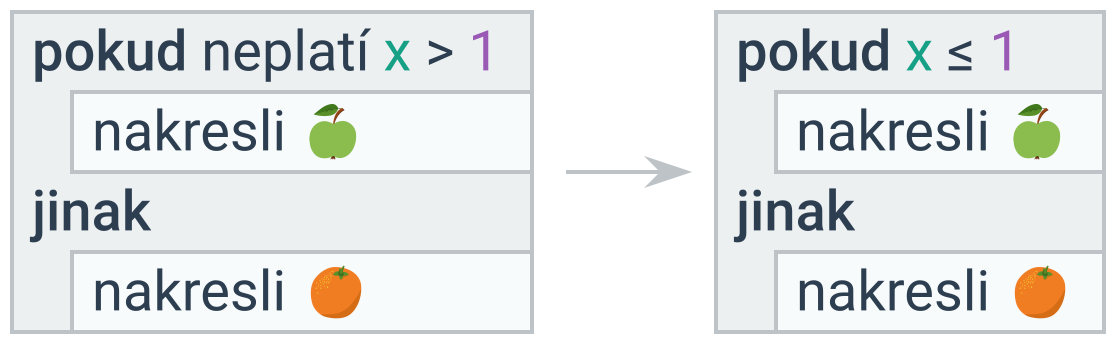
Nevhodný typ cyklu
Pokud je počet opakování dopředu známý, použijeme cyklus s daným počtem opakování, který je jednodušší.
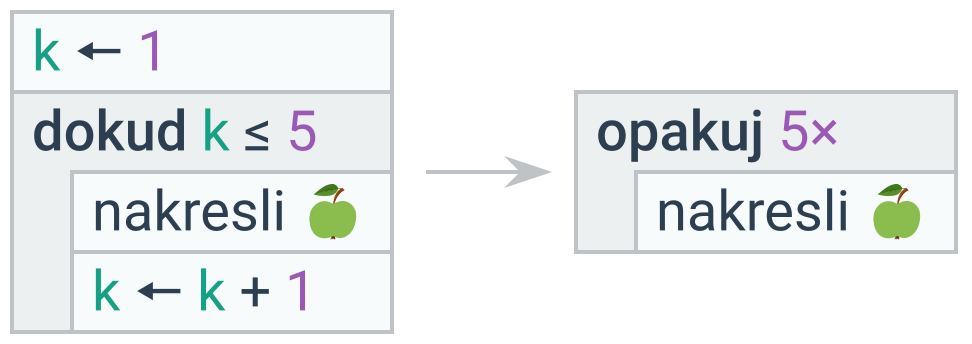
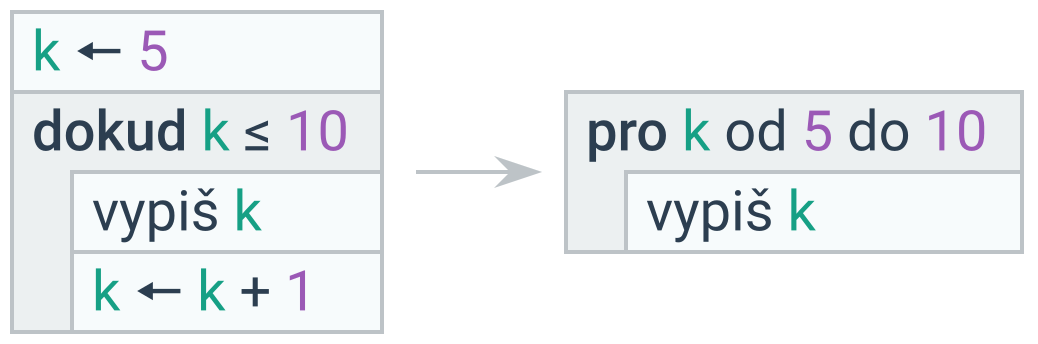
Cyklus místo podmíněného příkazu
Pokud se má příkaz provést nejvýše jednou, použijeme podmíněný příkaz, nikoliv cyklus.

Chybějící rozklad
Pokud je hlavní program nebo některá funkce příliš složitá, je vhodné program nebo funkci rozložit do více funkcí tak, aby každá funkce měla jasný účel.
Duplicitní kód
Pokud se v programu opakují stejné nebo podobné kousky kódu, program to nejen zbytečně natahuje, ale také to komplikuje jeho úpravy – je potřeba změnit více míst (a pokud některé místo upravit zapomeneme, zaneseme do programu chybu).
Duplicitní úseky kódu
Pokud jsou dva úseky kódu hodně podobné, lze je často zobecnit do společné pomocné funkce.

Duplicitní příkazy v posloupnosti
Posloupnost stejných příkazů lze nahradit cyklem. Cyklem lze nahradit také posloupnost příkazů, které se liší pouze hodnotou proměnné, která se mění pořád stejným způsobem.
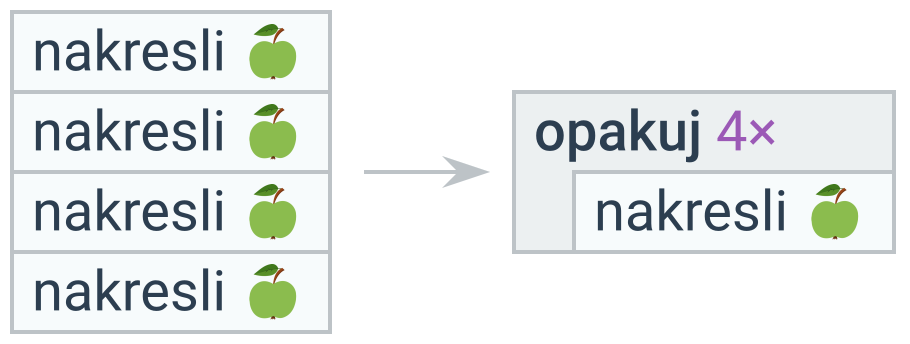
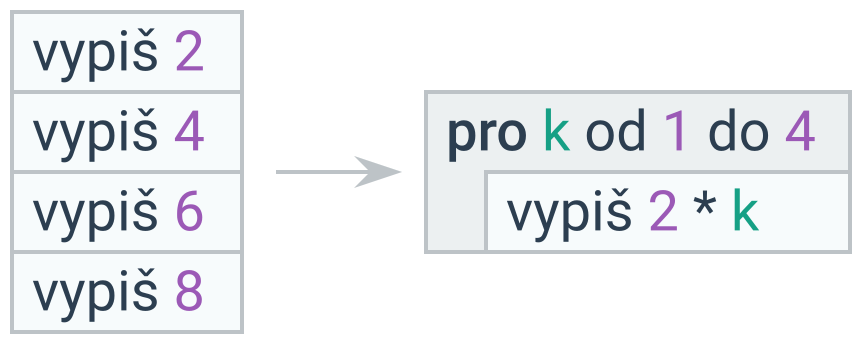
V některých případech nepotřebujeme zavádět nový cyklus, ale upravit stávající.
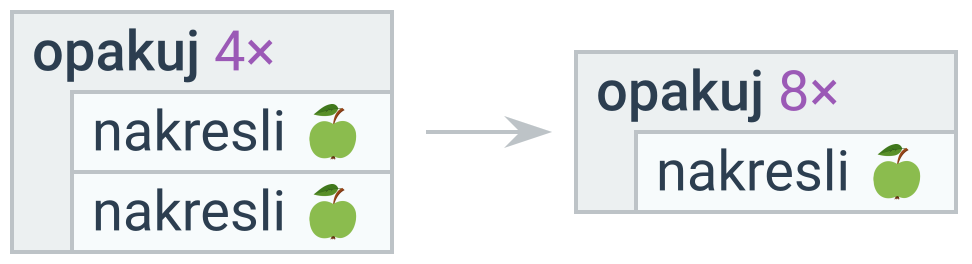
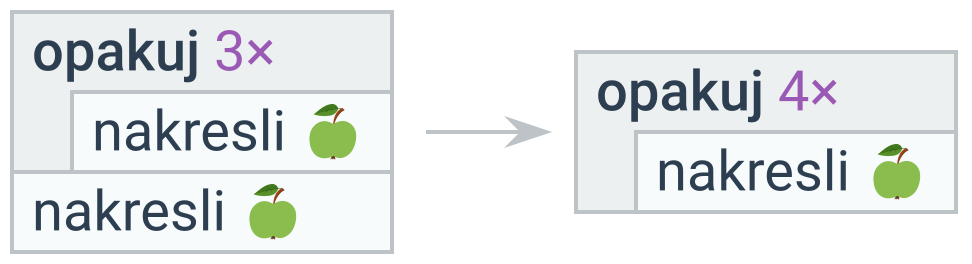
Duplicity v těle podmíněných příkazů
Pokud mají po sobě jdoucí větve podmíněného příkazu úplně stejné tělo, lze je spojit využitím složené podmínky.
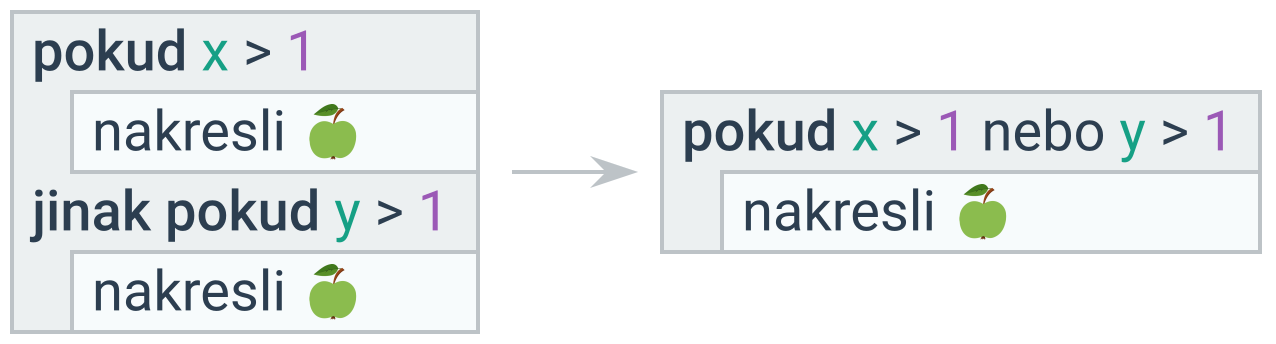
Když se těla liší, ale máme na začátku / na konci všech větví podmíněného příkazu stejný příkaz (nebo více stejných příkazů), lze tento příkaz přesunout před/za podmíněný příkaz.
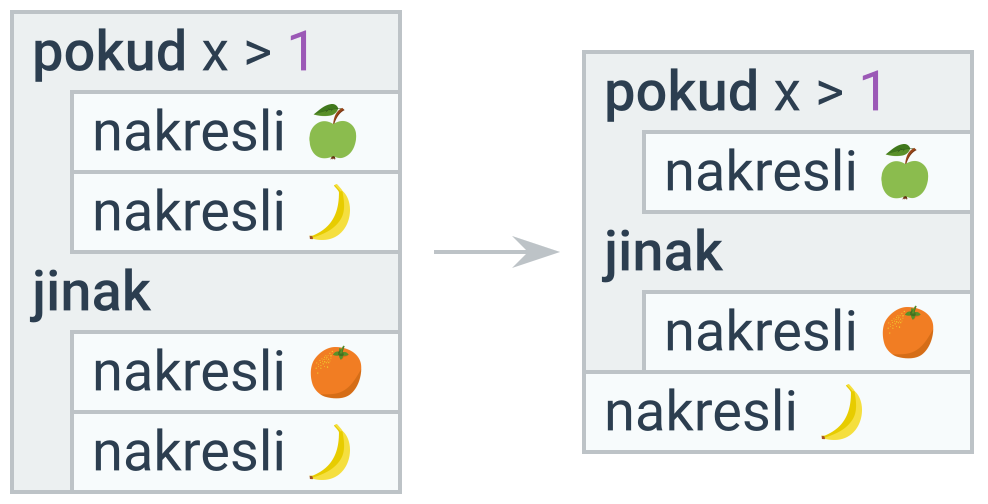
Pokud všechny větve podmíněného příkazu obsahují cyklus se stejnou hlavičkou, lze se duplicity zbavit přesunutím podmíněného příkazu dovnitř cyklu.
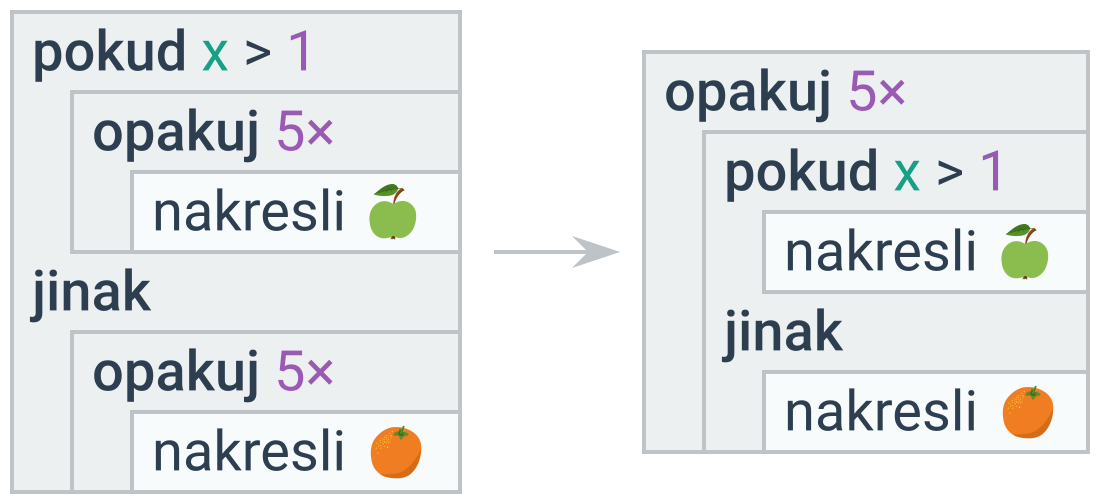
Nevhodná jména
Nevhodně zvolená jména proměnných a funkcí komplikují pochopení programu a nezřídka vedou k chybám při psaní programu (nebo při jeho pozdějším rozšiřování).
Nepopisná jména
Volíme taková jména, která jasně vyjadřují účel proměnné či funkce, i za cenu delšího názvu. Jednopísmenné názvy jsou vhodné jen v omezených případech (řídící proměnná cyklu, souřadnice bodu, krátké ukázky kódu).
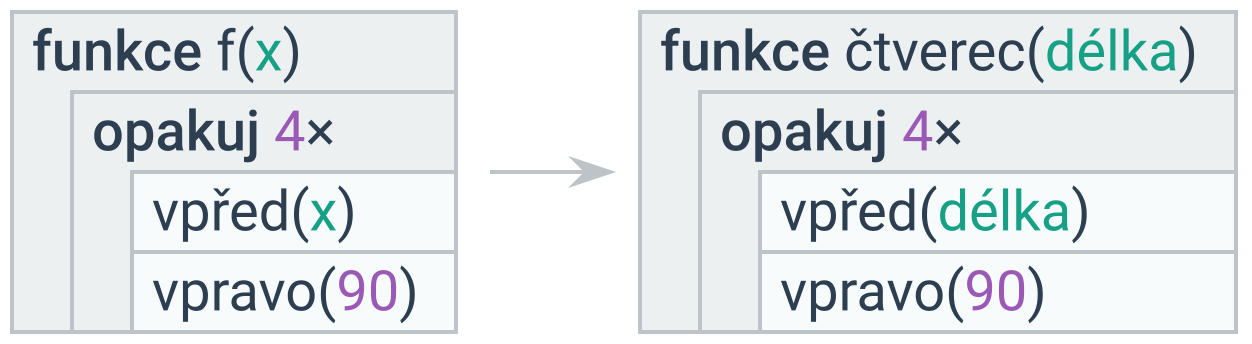
Zavádějící jména
Ještě nebezpečnější než jména nepopisná jsou jména, která vypadají popisně, ale popisují proměnnou či funkci chybně.
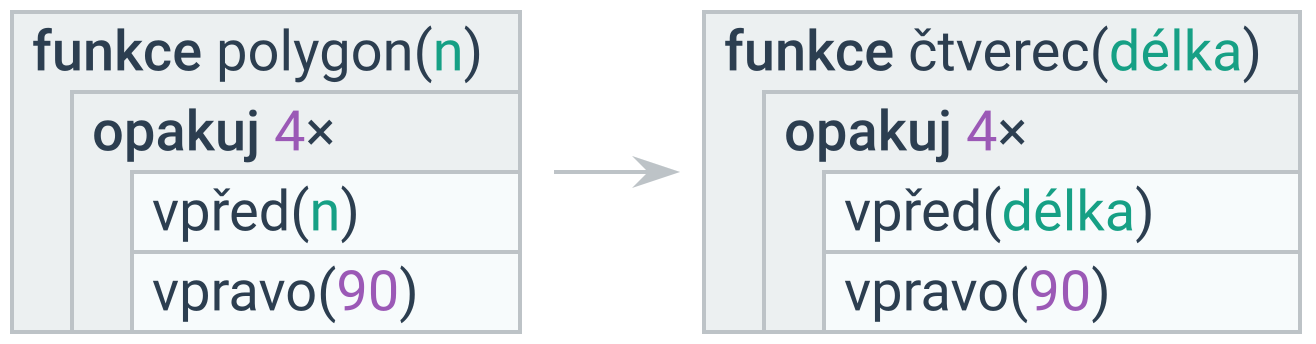
Překrývající se jména
V rámci jednoho kontextu není vhodné použít jedno jméno pro více různých věcí – ani v případě, že se už na původní proměnnou odkazovat nepotřebujeme. Takové překrývání komplikuje pochopení programu a vede k chybám při jeho úpravách.
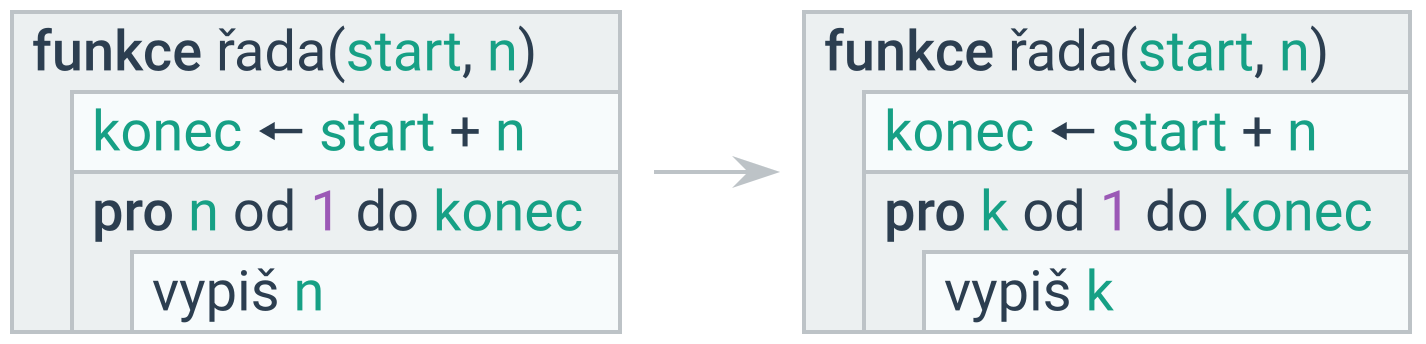
Vývojové diagramy
Vývojové diagramy představují způsob, jak můžeme graficky reprezentovat postup nebo návod pro nějakou činnost. Takový postup může být například recept na bábovku, návod na sestavení skříně nebo i počítačový program. Grafická reprezentace nám umožňuje lépe vidět místa, kde se návod větví na více možností (vyhodnocení podmínky u pokud, dotaz na typ spotřebiče), a kde můžeme očekávat cykly (příkaz dokud, opakování pro každý z muffinů).
Základní prvky vývojového diagramu
Každý příkaz programu (například přiřazení nebo výpis) reprezentujeme jako samostatný obdélník. Dva po sobě jdoucí příkazy spojíme šipkou ve směru provádění programu.
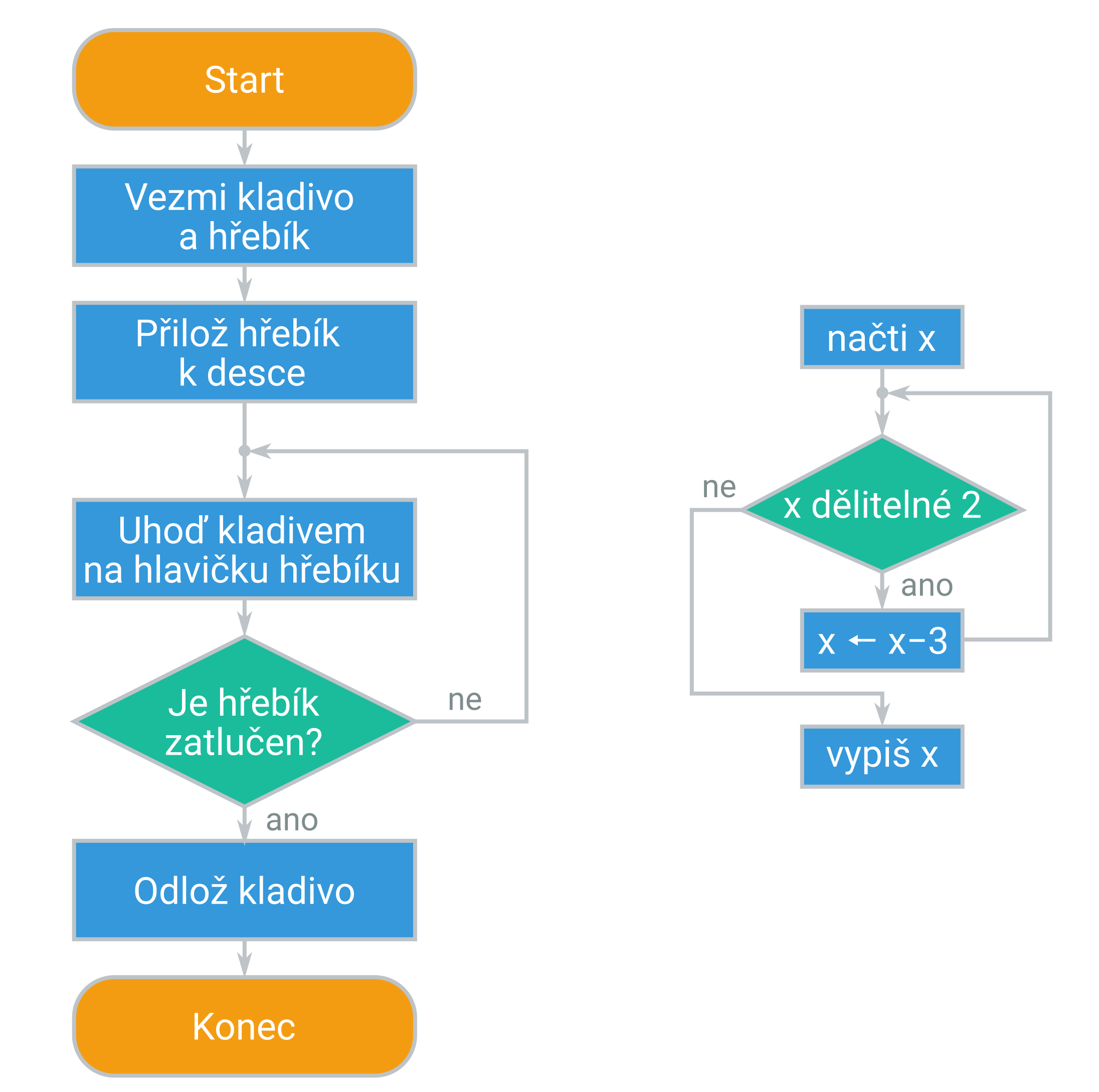
Podmínky nebo obecně místa, kde se tok programu větví na více možných cest, značíme kosočtvercem. Z nich pak vedou dvě šipky, jedna označená „ano“ nebo „pravda“, druhá „ne“ nebo „nepravda“.
Podmínky mohou být použity pro samostatné větvení, nebo jako součást cyklu. Podmínku může mít cyklus na začátku, jak ukazuje diagram programu, nebo na konci, jak ukazuje příklad se zatloukáním hřebíku. Šipka vedoucí z posledního příkazu cyklu vede před první příkaz tohoto cyklu. V takovém případě by vedlo více šipek do jednoho bloku, čemuž se obecně snažíme vyhnout. Vyřešíme to tak, že obě vstupní šipky spojíme plným kolečkem.
Pokud chceme znázornit, že diagram znázorňuje celý program a ne jen jeho část, můžeme přidat prvky „start“ a „konec“, které zakreslíme do obdélníků s oblými rohy.
Podobnost s jinými modely
Kromě vývojových diagramů máme i kapitolu na entitně-vztahové modely. Hlavním rozdílem je, že vývojový diagram zobrazuje posloupnost, v jaké se provádí jednotlivé kroky postupu, zatímco entitně-vztahový diagram popisuje vztah a vlastnosti mezi objekty.
Kromě vývojových diagramů a entitně-vztahových modelů můžeme vztahy nebo cesty mezi objekty znázorňovat například i pomocí grafů.
Nahoru
